
Lecture 10:Radiation
Lecture 10: Radiation

Introduction 目 Definition:energy emitted by matter that is at an infinite temperature Nature of thermal radiation ■ all matters radiate it is dependent on the temperature and nature of the material The Electromagnetic Spectrum
Introduction Definition: energy emitted by matter that is at an infinite temperature Nature of thermal radiation all matters radiate it is dependent on the temperature and nature of the material The Electromagnetic Spectrum

X Rays Microwave Gamma rays hermal radiation L 105 104 10-3 10-2 101 10 102 103 10 2(4m) FIGURE 12.3 Spectrum of electromagnetic radiation

Frequency and wavelength of the electromagnetic waves V=c/λ Transparent,semitransparent,and opaque materials Two features:spectral and directional distribution
Frequency and wavelength of the electromagnetic waves Transparent, semitransparent, and opaque materials Two features: spectral and directional distribution ν = c / λ

Blackbody Radiation ▣An ideal surface Absorbs all incoming radiation; Emits the maximum radiation at the same temp. No reflection,no transmission Radiation independent of direction: diffuse emitter
Blackbody Radiation An ideal surface Absorbs all incoming radiation; Emits the maximum radiation at the same temp. No reflection, no transmission Radiation independent of direction: diffuse emitter

Continued The Plank Distribution Eba C lecstar C1=3.742*108w:4m4/m2 C2=1.438*104um·K Whenλ=const T1一EAb↑
Continued The Plank Distribution [ 1] 5 / 1 2 − = b C T e C E λ λ λ C m K C w m m = ⋅ = ⋅ μ μ 4 2 8 4 2 1 1.438 *10 3.742 *10 / When λ=const T Eλ,b

Continued Wien's Displacement Law AT=C3 C3=2897.8,Um·K Sun,at 5800K,as black body, λ=C3/5800K=0.5m max Visible Range
Continued Wien’s Displacement Law λmaxT = C3 C3 = 2897 .8μm ⋅ K Sun, at 5800K, as black body, λmax = C3 / 5800K = 0.5μm Visible Range
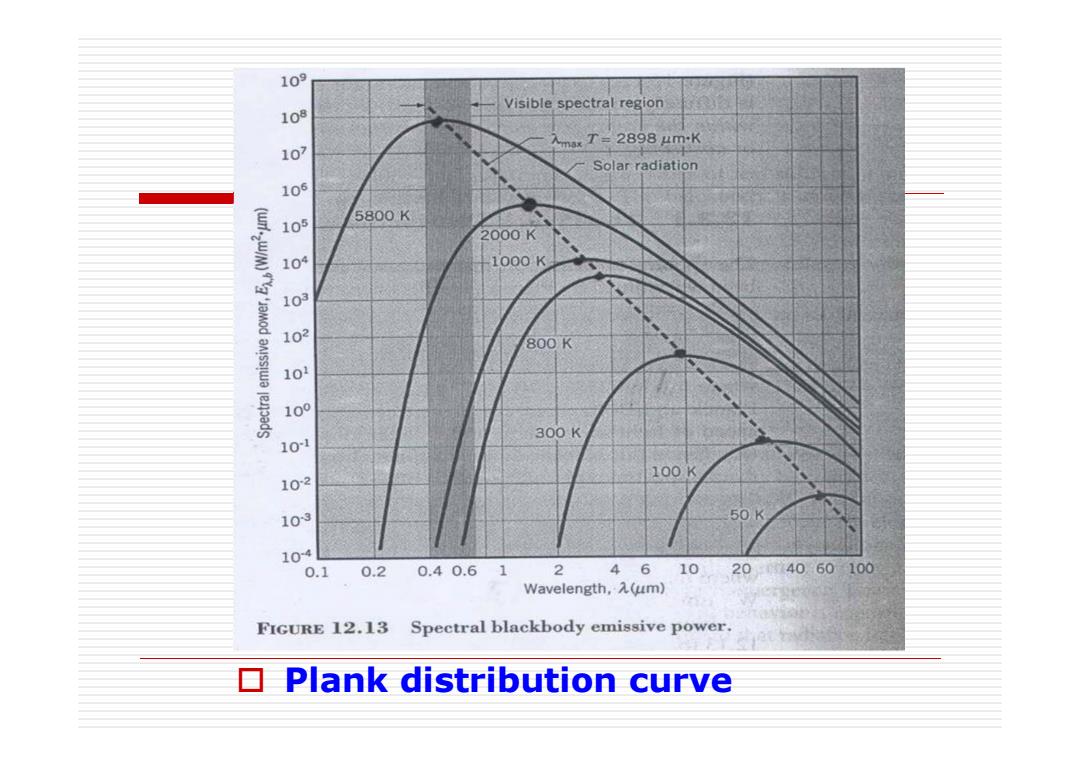
109 visible spectral region 入maxT=2898以m-K Solar radiation 10 5800K 2000K 104 1000K 800K 10 300K 100K 102 10-3 50K 104 0.1 0.2 0.40.6 1 2 46 10 20 4060100 Wavelength,入(um) FIGURE 12.13 Spectral blackbody emissive power. Plank distribution curve
Plank distribution curve

Continued ▣Total Emissive Power E=fExda=l C exp(C2/λT)I刂 ◇E6=o4 0=5.67*10-8W/m2.K4 ▣Band Emission
Continued Total Emissive Power Band Emission ∞ ∞ − = = 0 0 2 5 1 , [exp( / ) 1] λ λ λ λ λ d C T C Eb E bd 4 Eb =σT 8 2 4 = 5.67*10 W / m ⋅K − σ

Real Surface Radiation 目 Emissivity E(,T) Spectral E(T) emissivity Eō(2,T月 E(T total emissivity E=」E(,T)dM 广cE(,IdM c,Eu(,T))d几 £= OT4 E(T)=OT4 e=1 Blackbody
Real Surface Radiation Emissivity λ λ λ ε λ λ = ( , ) ( , ) E , T E T b = ε ( ) ( ) E T E T b ∞ ∞ = = 0 , 0 ( , ) ( ) ( , ) ε λ λ λ λ λ λ λ E T d E T E T d b 4 Eb ( T ) = σT 4 0 , ( , ) T E T d b σ ε λ λ ε λ λ ∞ = ε = 1 Blackbody total emissivity Spectral emissivity