
Lecture 3 Apply Energy Conservation Equation
Lecture 3 Apply Energy Conservation Equation

Energy Conservation Equation Control Volume out E st En+E。-Eom=dEu/dt=Et The rate at which thermal and mechanical energy enters a control volume,minus that leaving out,plus the rate at which thermal energy is generated within the control volume,should equal the rate of increase of energy stored within the control volume
Energy Conservation Equation in g out st Est E E E dE dt + − == = The rate at which thermal and mechanical energy enters a control volume, minus that leaving out, plus the rate at which thermal energy is generated within the control volume, should equal the rate of increase of energy stored within the control volume. Control Volume Ein Eout E g Est

Procedure: Define appropriate control volume with the control surface ldentify appropriate time basis Identify relevant energy processes Write conservation equation
Procedure: • Define appropriate control volume with the control surface • Identify appropriate time basis • Identify relevant energy processes • Write conservation equation
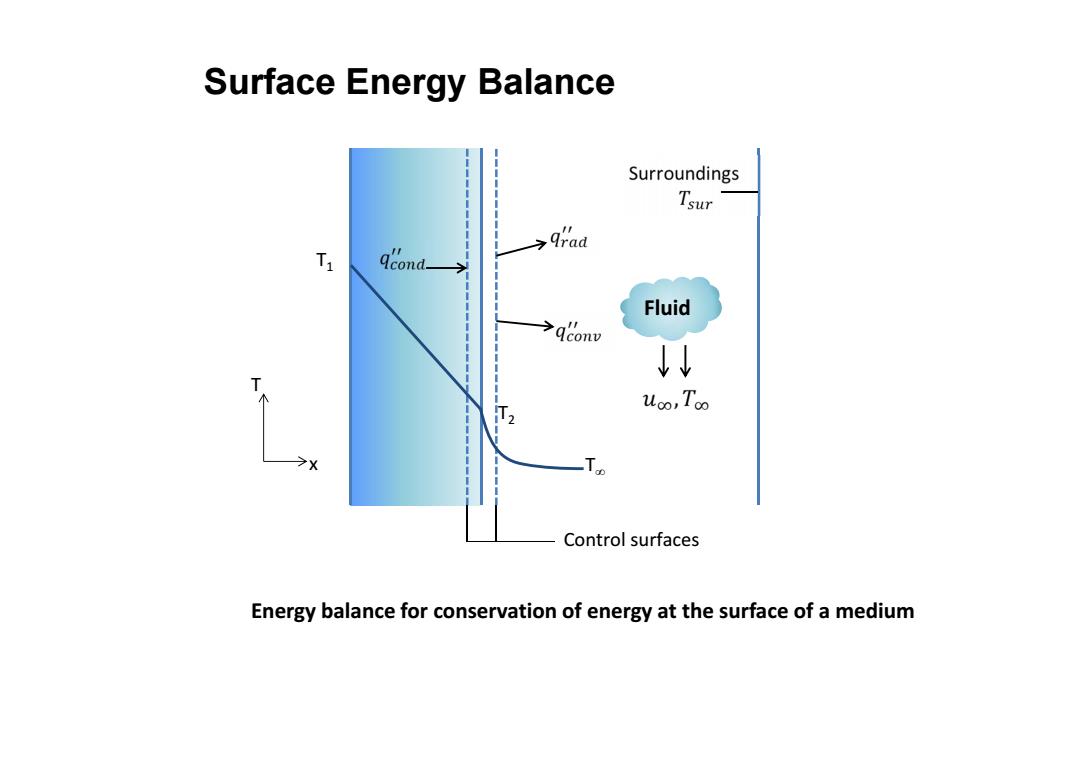
Surface Energy Balance Surroundings Tsur 9gaa qcond Fluid qconv ↓ T uoo,To Control surfaces Energy balance for conservation of energy at the surface of a medium
Surface Energy Balance T1 T2 T x T ∞ Control surfaces Fluid Energy balance for conservation of energy at the surface of a medium

Ein-Eout =0 Conduction from the medium to the control surface Qcond Convection from the surface to a fluid qconv Net radiation exchange from the surface to the surroundings qrad Energy Balance: qcond -qconv -qrad =0
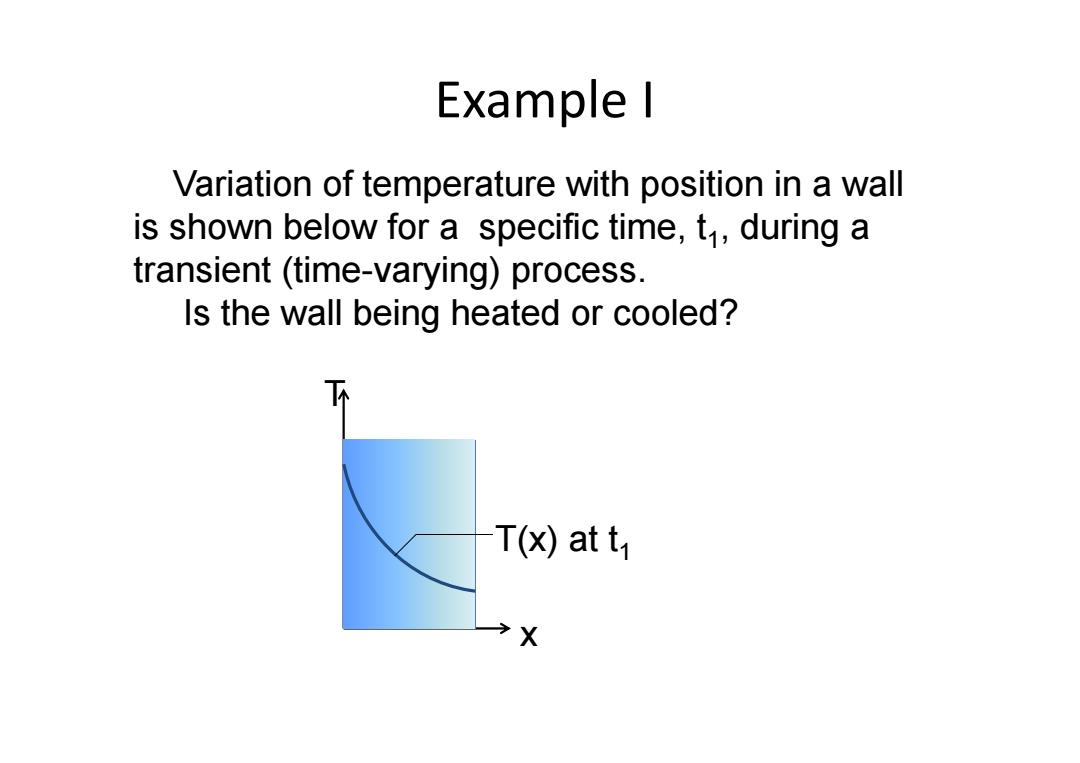
Example I Variation of temperature with position in a wall is shown below for a specific time,t1,during a transient(time-varying)process. Is the wall being heated or cooled? T(x)at t X
Variation of temperature with position in a wall is shown below for a specific time, t 1, during a transient (time-varying) process. Is the wall being heated or cooled? T x T(x) at t 1 Example I

Example 2 The power supplied to a heating pad which measures 1cm*1cm is 0.02w.The pad is mounted the surface of human surface (a flat plate)and is allowed to exchange heat by free convection to the surrounding air at 26C.The heat transfer coefficient for this configuration is 8 w/m2.C.Safety considerations require that the surface temperature not exceed 45C.Should the heating be operated under these conditions?
Example 2 • The power supplied to a heating pad which measures 1cm*1cm is 0.02w. The pad is mounted the surface of human surface (a flat plate) and is allowed to exchange heat by free convection to the surrounding air at 26oC. The heat transfer coefficient for this configuration is 8 w/m2·oC. Safety considerations require that the surface temperature not exceed 45oC. Should the heating be operated under these conditions?

·Observations Schematic diagram The Electrical energy dissipated in the transistor is transferred to the surface by conduction and then added to the surrounding air by convection. Heat is also removed from the surface by radiation. -For heat to transfer from the surface to the surrounding air, surface temperature must be higher than ambient temperature The higher the dissipated power,the higher its surface temperature
• Observations – Schematic diagram – The Electrical energy dissipated in the transistor is transferred to the surface by conduction and then added to the surrounding air by convection. – Heat is also removed from the surface by radiation. – For heat to transfer from the surface to the surrounding air, surface temperature must be higher than ambient temperature – The higher the dissipated power, the higher its surface temperature

·Problem Definition Finding a relationship between the power of the transistor and its surface temperature 。Solution plan Apply Newton's law of cooling to the surface of the transistor
• Problem Definition – Finding a relationship between the power of the transistor and its surface temperature • Solution plan – Apply Newton’s law of cooling to the surface of the transistor

。Plan execution -Assumptions ·Steady state All the electric energy dissipated in the heat pad leaves its surface(no energy leaves from the back side) Negligible Radiation Uniform surface temperature,heat transfer coefficient and constant ambient temperature
• Plan execution – Assumptions • Steady state • All the electric energy dissipated in the heat pad leaves its surface (no energy leaves from the back side) • Negligible Radiation • Uniform surface temperature, heat transfer coefficient and constant ambient temperature