
Lecture 4 Heat Conduction Equation
Lecture 4 Heat Conduction Equation

q:=-kA dT -Fourier's Law dx Three dimensional heat flow -k qy 7
x T q '' x ∂ ∂ = − k y T q '' y ∂ ∂ = − k z T q '' z ∂ ∂ = − k Three dimensional heat flow ——Fourier’s Law dx dT q x = − kA
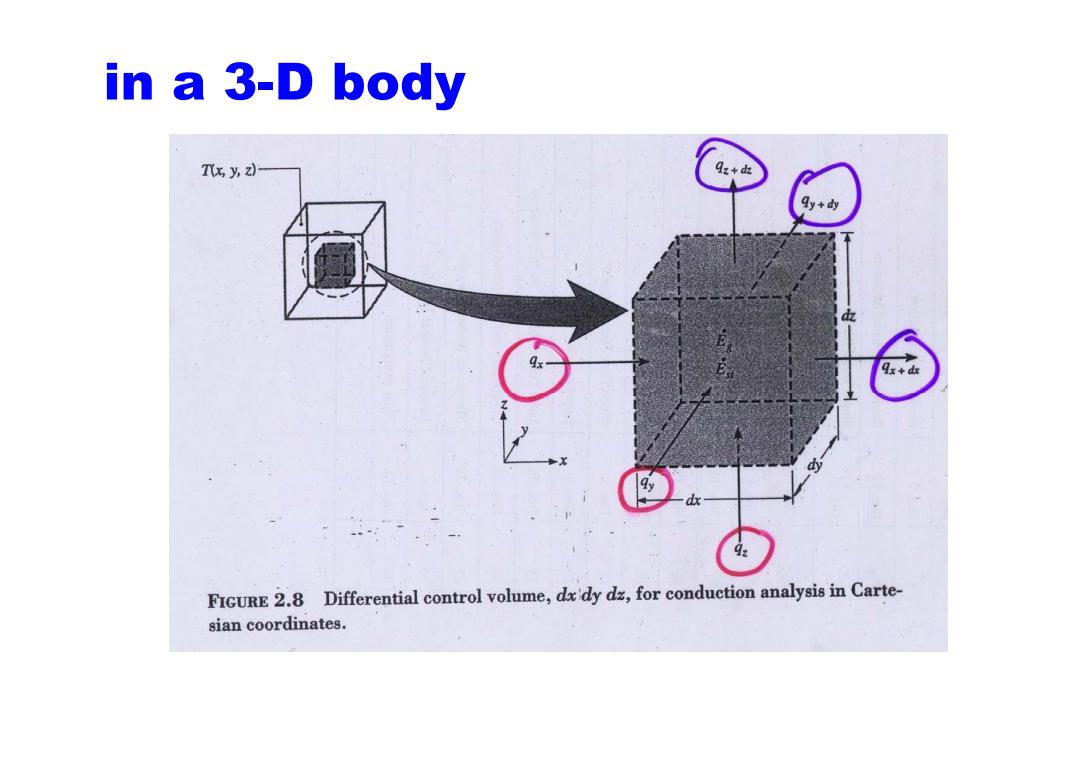
in a 3-D body Ts y,2)- 9z+血 y+dy 0 4: FIGURE 2.8 Differential control volume,dx'dy dz,for conduction analysis in Carte- sian coordinates
in a 3-D body

Energy Balance Eu+Ea-Eou =Est xdyd g+gy+g-+qdxdyd=-gx4-gxvy-:v=Pc,di dx daydy-d北 gd+gdxdyd==pCr di dxdyd- 9s=-kdydz aT dx gy =-kdxdz OT dy 9:=-kdxdy aT d
.. . . Ein q out st +− = EE E Energy Balance . x y z x dx y dy z dz p T q q q q dxdydz q q q c dxdydz dt +++ ρ ∂ +++ − − − = x T q kdydz dx ∂ = − y T q kdxdz dy ∂ = − z T q kdxdy dz ∂ = − . x y z p q q q T dx dy dz q dxdydz c dxdydz dx dy dz dt ρ ∂ ∂ ∂ ∂ −−−+ =

In Cartesian coordinate systems: In Cylindrical coordinate systems: In spherical coordinate systems: o 1=kV2T+g
2 ''' p T C kTq t ρ ∂ =∇ + ∂ In Cartesian coordinate systems: In Cylindrical coordinate systems: In spherical coordinate systems:

It is valid at every point in the material It is the heat equation for conduction in isotropic,constant conductivity material -Further simplifications: ·Steady state ·One dimensional ·No energy generation
It is valid at every point in the material It is the heat equation for conduction in isotropic, constant conductivity material Further simplifications: Steady state One dimensional No energy generation

Qz+dz rdo Qo+do dz Tro.z) gr+dr qr
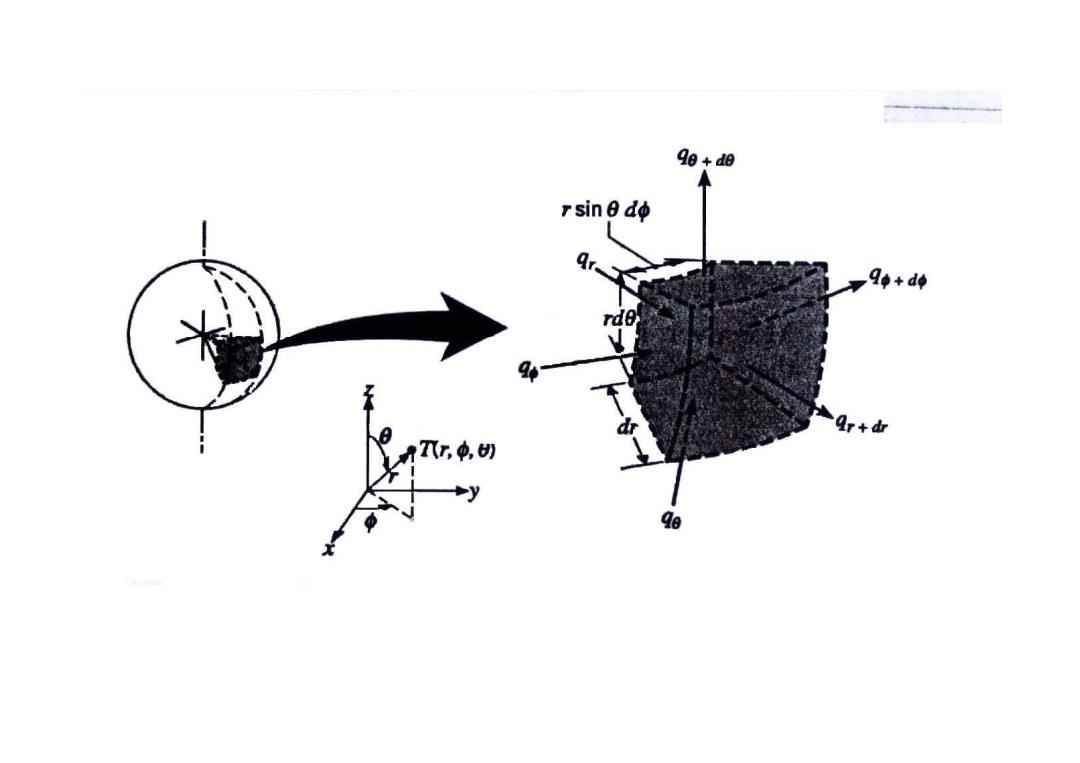
90+dB r sin a dφ 9o+do rde Ar+dr Tr,,切 Qe

Boundary Conditions and nitia Conditions Fixed surface temperature ■Fixed heat flux ·insulated boundary Convection -Interface
Boundary Conditions and Initial Conditions Fixed surface temperature Fixed heat flux insulated boundary Convection Interface