
Lecture 5 Conduction equation and examples
Lecture 5 Conduction equation and examples
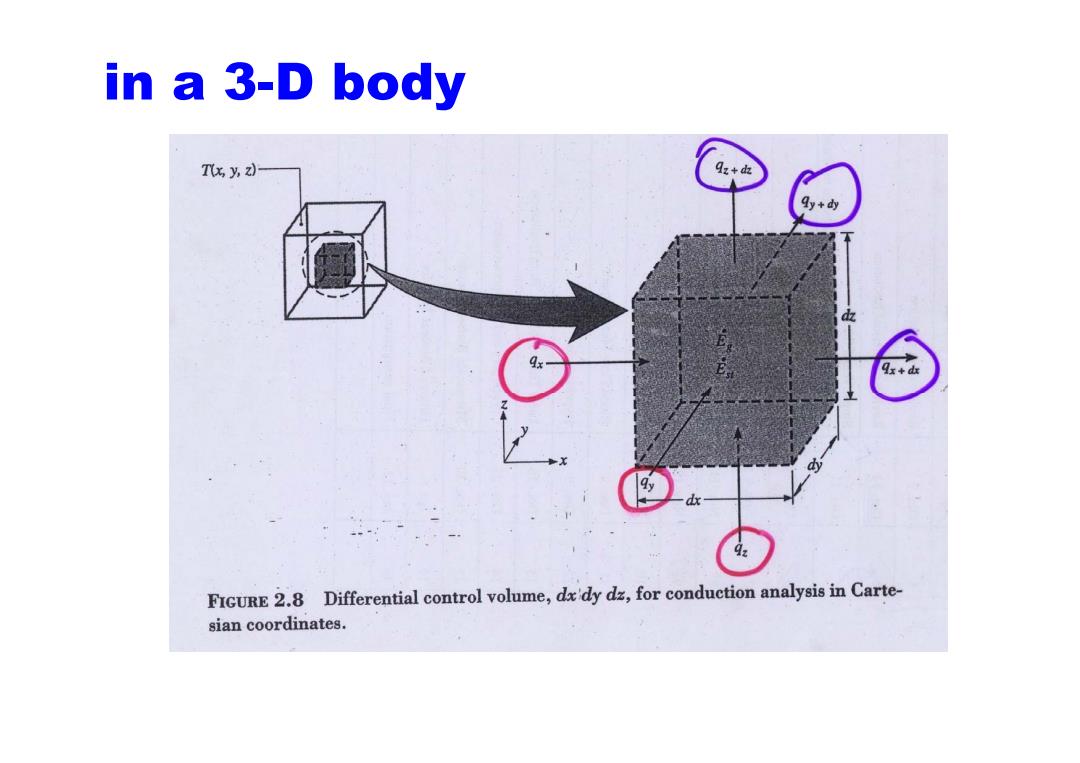
in a 3-D body Ts y,2)- 9z+血 y+dy 0 4: FIGURE 2.8 Differential control volume,dx'dy dz,for conduction analysis in Carte- sian coordinates
in a 3-D body

Energy Balance Ein+Ea-Eou Es dxdydz q4.+,+q.+9ddb-9r+h-9,+-9:+t=pe,dt oa;dx dy Tdxdyd dx ∂ay dy-d正 dqdxdyd=pcC aT 9s =-kdydz 9y =-kdxdz aT 新 q:=-kdxdy aT (k )* a x (k dy * y kT)+q
.. . . Ein q out st +− = EE E Energy Balance . x y z x dx y dy z dz p T q q q q dxdydz q q q c dxdydz dt +++ ρ ∂ +++ − − − = x T q kdydz dx ∂ = − y T q kdxdz dy ∂ = − z T q kdxdy dz ∂ = − . x y z p q q q T dx dy dz q dxdydz c dxdydz dx dy dz dt ρ ∂ ∂ ∂ ∂ −−−+ = ( ) ( ) ( ) ''' p TT T T C k k kq txx yy z z ρ ∂ ∂∂ ∂∂ ∂∂ =+++ ∂∂ ∂ ∂ ∂ ∂ ∂

In Cylindrical coordinate systems: pC. T=kV2T+g" pC. T =kV2T+9" dt ∂T=kVT+g
2 ''' p T C kTq t ρ ∂ =∇ + ∂ In Cylindrical coordinate systems: 2 ''' p T C kTq t ρ ∂ =∇ + ∂ 2 ''' p T C kTq t ρ ∂ =∇ + ∂
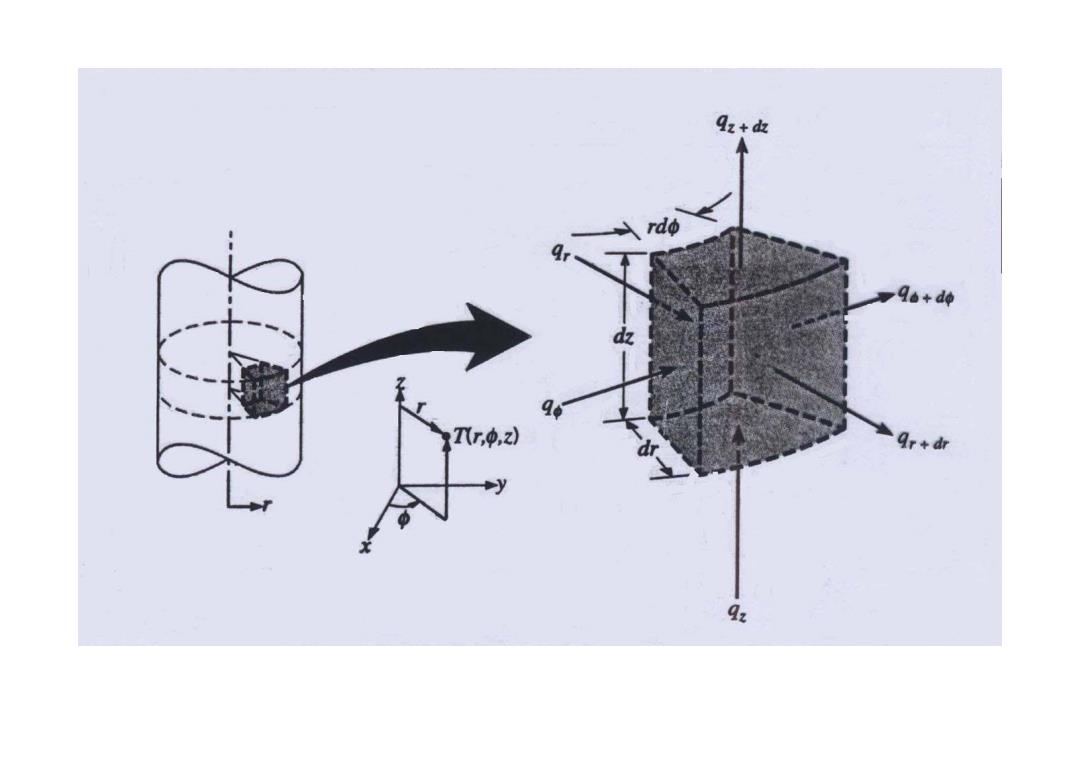
Qz+dz rdo Qo+do dz Tro.z) gr+dr qr

In spherical coordinate systems: General form PCp T =k72T+9" dt
In spherical coordinate systems: ( ) ( ) ( ) ''' p TT T T C k k kq txx yy zz ρ ∂ ∂∂ ∂∂ ∂∂ =+++ ∂∂ ∂ ∂ ∂ ∂ ∂ 2 ''' p T C kTq t ρ ∂ =∇ + ∂ General form