
Lecture 5 Conduction equation and examples 孙建奇
Lecture 5 Conduction equation and examples 孙建奇
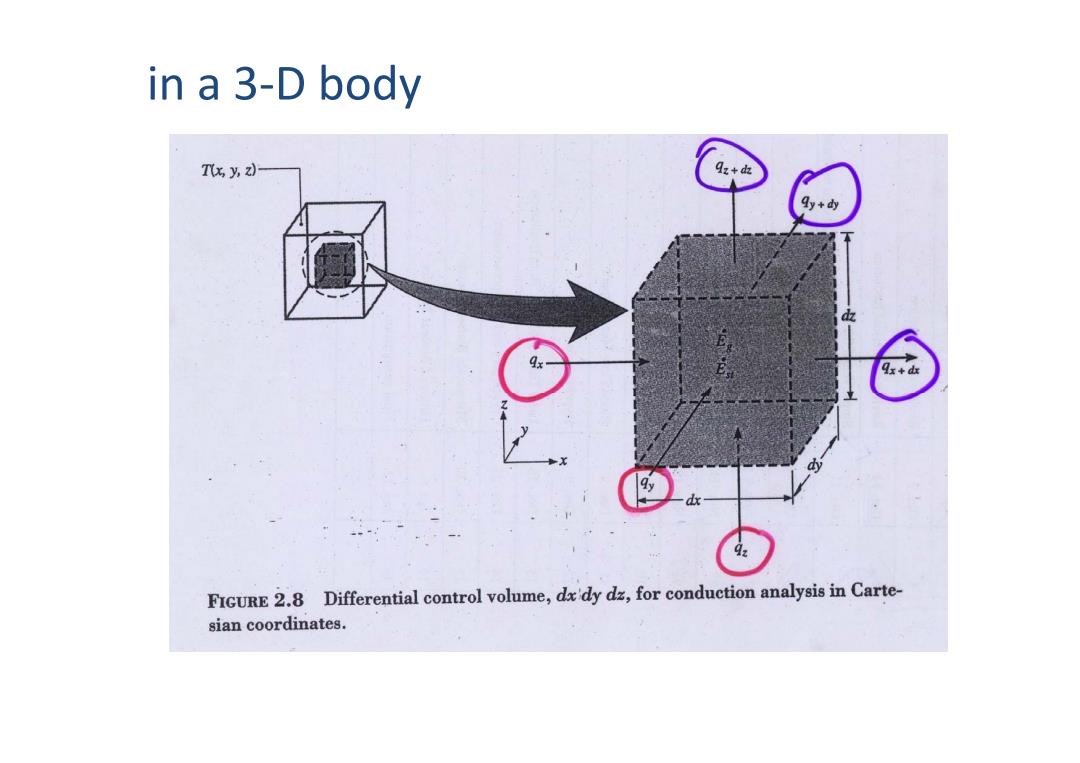
in a 3-D body Tx y,2)- Qz+de y+dy dx 4: FIGURE 2.8 Differential control volume,dx'dy dz,for conduction analysis in Carte- sian coordinates
in a 3-D body

。Energy Balance Ein+Ea Eou =Est Tdxdydz q4.+,+q.+9ddb-9r+h-9,+-9:+t=per oa;dx dy dx ∂a dy-d正 T dxdyd qdxdyd=pc,di aT 9s =-kdydz dx 9,=-hdrde O dy OT g:=-kaxdy dz ∂T ∂ (k 一)+ (k ay )+ dy z 3T)+4
.. . . Ein q out st +− = EE E • Energy Balance . x y z x dx y dy z dz p T q q q q dxdydz q q q c dxdydz dt +++ ρ ∂ +++ − − − = x T q kdydz dx ∂ = − y T q kdxdz dy ∂ = − z T q kdxdy dz ∂ = − . x y z p q q q T dx dy dz q dxdydz c dxdydz dx dy dz dt ρ ∂ ∂ ∂ ∂ −−−+ = ( ) ( ) ( ) ''' p TT T T C k k kq txx yy zz ρ ∂ ∂∂ ∂∂ ∂∂ =+++ ∂∂ ∂ ∂ ∂ ∂ ∂
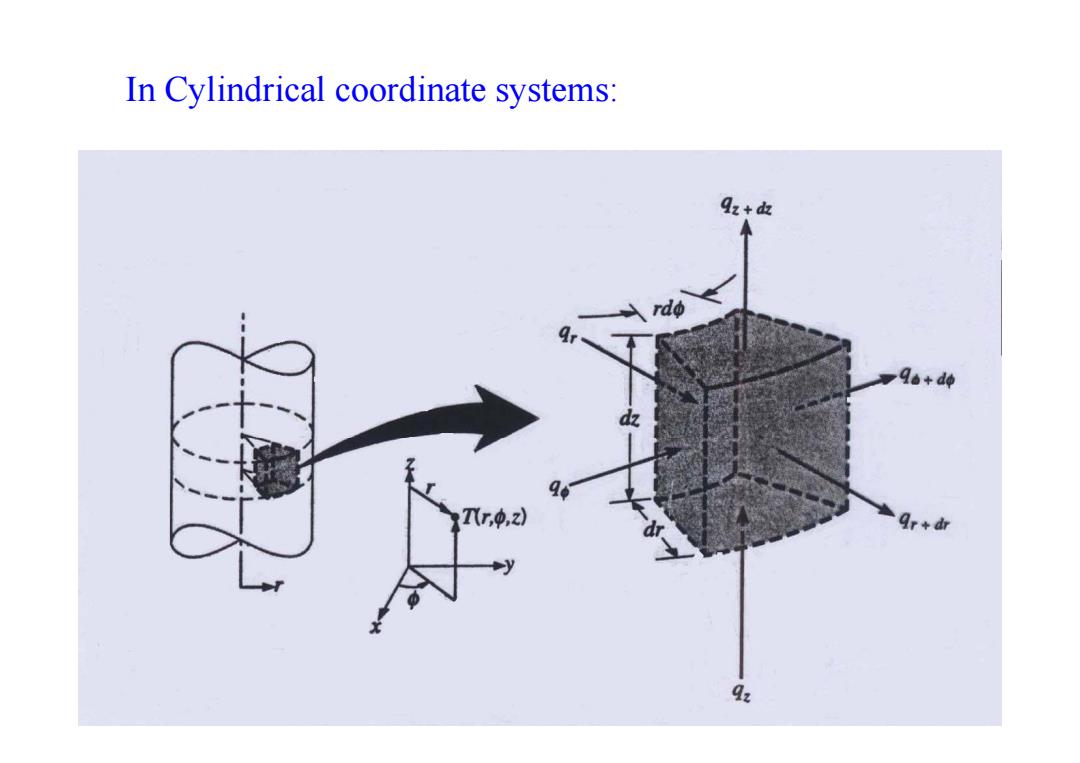
In Cylindrical coordinate systems: qz+血 Qa+do d Tr,z) 9r+d由 Qx
In Cylindrical coordinate systems:

In Cylindrical coordinate systems: OT 1a aT、,ka2T,,a2T pcp-(ra+0+k2+g” Boundary conditions: T(ro)=T1 -k81。=9g-k80=0 aT -k8n=hs-T)
In Cylindrical coordinate systems: Boundary conditions:

In spherical coordinate systems: pc部-点品r部+点+点品0+” k a2T k d OT General form ∂T=kV2T+g
In spherical coordinate systems: 2 ''' p T C kTq t ρ ∂ =∇ + ∂ General form

For a person of 80 kg weight and 1.8 m height the skin area is approximately 2 m2.For typical values of k=0.4 W/m-C,(Te-Ts)=4C,and L=4 cm=0.04 m.What is the steady state temperature distribution in the skin and the heat transferred at the skin surface?
For a person of 80 kg weight and 1.8 m height the skin area is approximately 2 m 2. For typical values of k=0.4 W/m·C, ( Tc-Ts )=4C, and L=4 cm=0.04 m. What is the steady state temperature distribution in the skin and the heat transferred at the skin surface?

Example 1.1:steady state conduction in one rectangular direction,x Let us model a section of the outer layers of the human body as a slab shown in figure with thickness,L,constant thermal conductivity,k;and no internal heat generation,blood flow,or useful work.Let us take for boundary conditions that the inner surface temperature,at x=0,is equal to the body's core temperature,T;and that the skin surface temperature,at x=L,is Ts,both of which are constant.We wish to find the steady state temperature distribution and the heat transferred at the skin surface. To Ts ax Core Skin Surface dx 0
Example 1.1: steady state conduction in one rectangular direction,x Let us model a section of the outer layers of the human body as a slab shown in figure with thickness, L, constant thermal conductivity, k; and no internal heat generation, blood flow, or useful work. Let us take for boundary conditions that the inner surface temperature, at x=0, is equal to the body’s core temperature, Tc; and that the skin surface temperature, at x=L, is Ts, both of which are constant. We wish to find the steady state temperature distribution and the heat transferred at the skin surface

=0 dx2 Boundary condition:X=0,T=T;x=L,T=Ts T=Cix+C2 X T-T-(To-T) =-kdT=kTe-Ts or qx= Ax dx L kAx (Te-T) L
or Boundary condition: x=0, T=Tc ; x=L, T=Ts
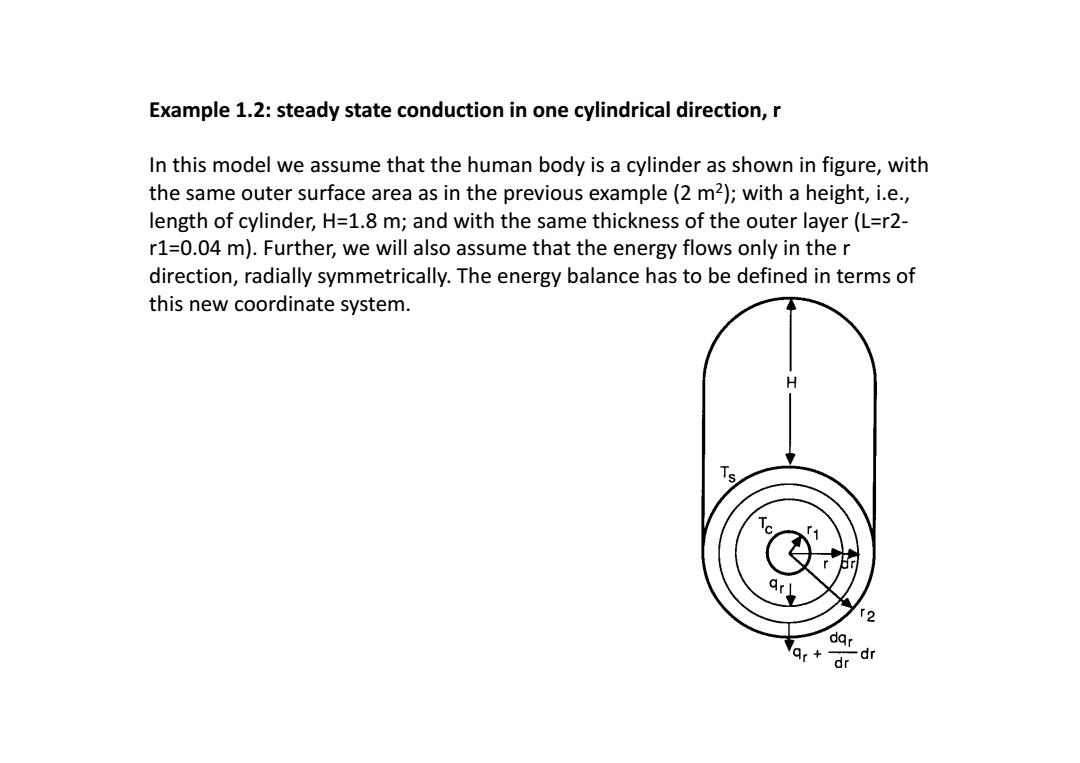
Example 1.2:steady state conduction in one cylindrical direction,r In this model we assume that the human body is a cylinder as shown in figure,with the same outer surface area as in the previous example(2 m2);with a height,i.e., length of cylinder,H=1.8 m;and with the same thickness of the outer layer(L=r2- r1=0.04 m).Further,we will also assume that the energy flows only in the r direction,radially symmetrically.The energy balance has to be defined in terms of this new coordinate system. H 人9 T2 dqr
Example 1.2: steady state conduction in one cylindrical direction, r In this model we assume that the human body is a cylinder as shown in figure, with the same outer surface area as in the previous example (2 m 2); with a height, i.e., length of cylinder, H=1.8 m; and with the same thickness of the outer layer (L=r2- r1=0.04 m). Further, we will also assume that the energy flows only in the r direction, radially symmetrically. The energy balance has to be defined in terms of this new coordinate system