
Lecture 11 Radiation Continued
Lecture 11 Radiation Continued

Radiation Intensity Solid angel dAn (8,p) co=2” dA =rsinede.rdo dw=sinadadΦ
Radiation Intensity – Solid angel 2 r dA d n ω = dA n = rsin θdθ ⋅rdφ dω = sin θdθdφ
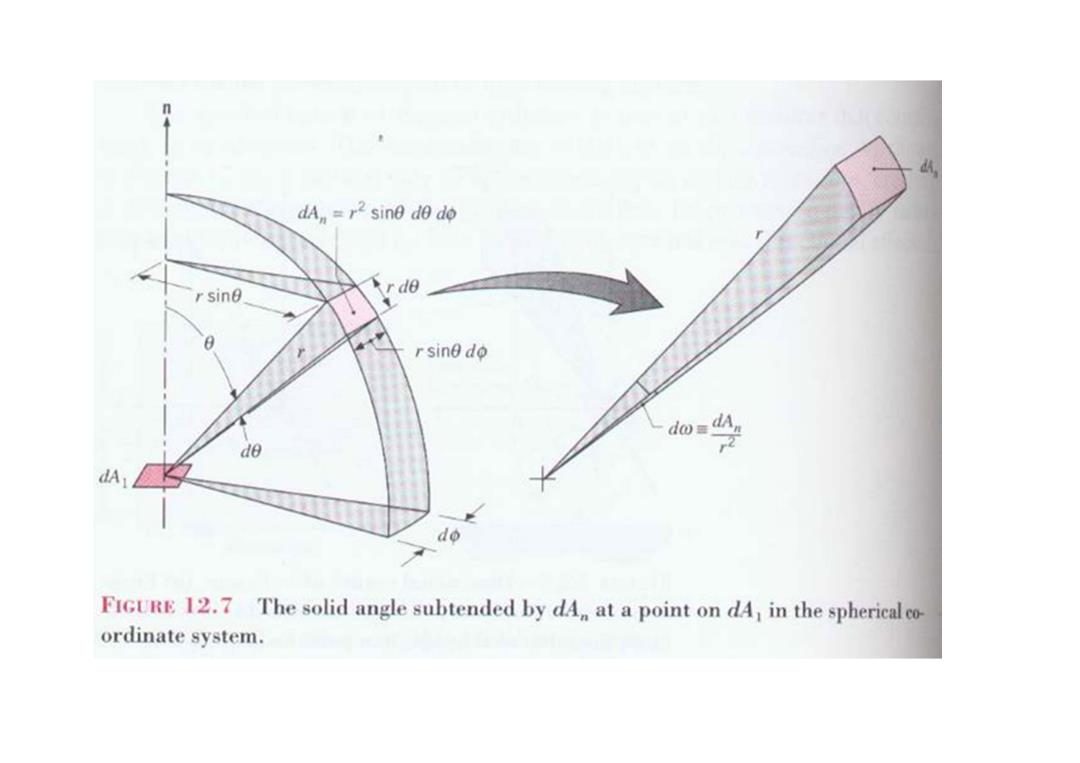
n dAn=r2sine de do rsine r de rsine do de dA do FIGURE 12.7 The solid angle subtended by dA at a point on dA,in the spherical co ordinate system

Radiation between two very small surfaces radiation Spectral intensity of the emitted Radiation:the rate at which radiant dAn energy is emitted at the wavelength in the direction ( per unit area of the emitting surface normal to this direction,per unit solid dAy angle,per unit wavelength interval 12(,0,0)= dq dA,cos adwdA (a)
• Radiation between two very small surfaces – Spectral intensity of the emitted Radiation: the rate at which radiant energy is emitted at the wavelength in the direction per unit area of the emitting surface normal to this direction, per unit solid angle, per unit wavelength interval θ λ λ λ θ φ dA dwd dq I e cos ( , , ) 1 , = λ (, ) θ ϕ
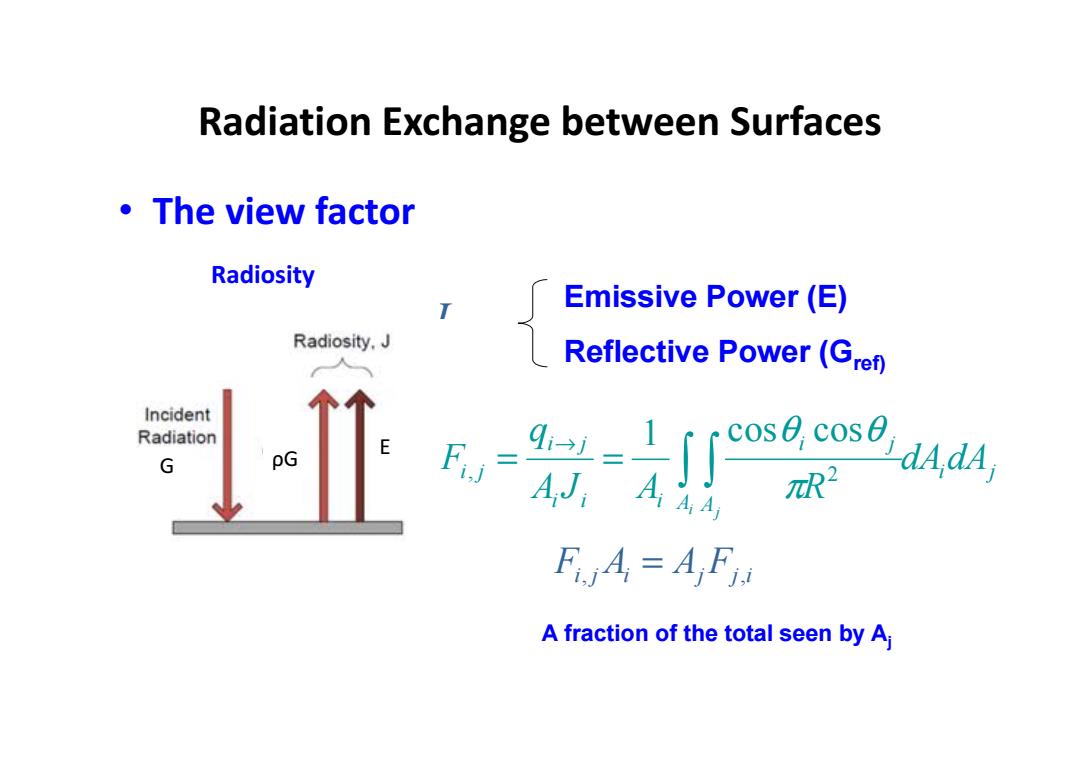
Radiation Exchange between Surfaces ·The view factor Radiosity Emissive Power (E) Radiosity.J Reflective Power (Gret) Incident Radiation G PG R2 FA=AF A fraction of the total seen by Aj
Radiation Exchange between Surfaces • The view factor Radiosity i J Emissive Power (E) Reflective Power (Gref) Fi, j Ai = Aj Fj,i A fraction of the total seen by Aj ρ G E G i j A A i j i i i i j i j dAdA A J A R q F i j = = → , 2 1 cos cos π θ θ
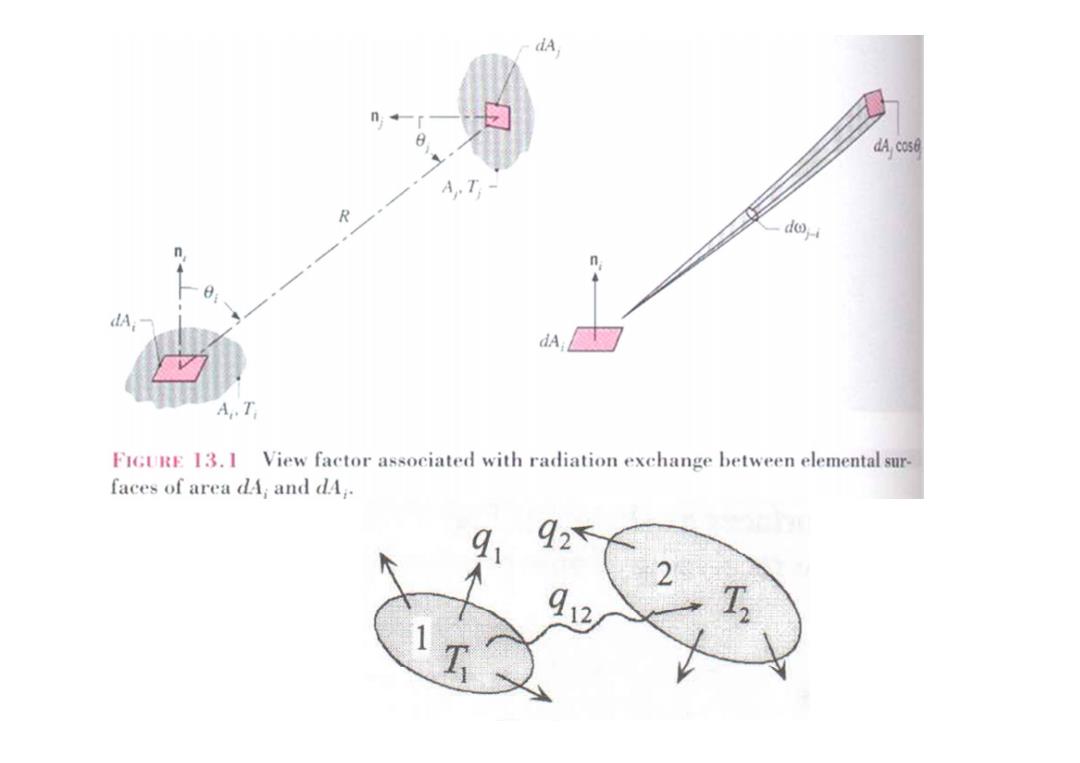
dA n 8 dA cos R do,i dA, dA A.T FIGURE 13.I View factor associated with radiation exchange between elemental sur- faces of area dA;and dA. 92< 2 02

Continued For enclosed surfaces ∑F=1 j=1 For concave surfaces F≠0
Continued For enclosed surfaces 1 1 , = = N j Fi j For concave surfaces 0 Fi,i ≠

For plane or convex surfaces F=0 Summation: A,=A+A2+.…An R,=2E
For plane or convex surfaces 0 Fi,i = Summation: Aj = A1 + A 2 + A n = = n k Fi j Fi k 1 ,

。Example Two parallel round plates A1 =A2,the distance is H,the radius of the plate is r,using the cases listed in the appendix, Please find Fs 3 (a)
• Example – Two parallel round plates A1 =A2, the distance is H, the radius of the plate is r, using the cases listed in the appendix, Please find F31

Blackbody Radiation Exchange qii=FiAJ q=FAJ If A &A are blackbody,no reflection, J=E=OT4 Net radiation heat transfer between the surfaces △q=FA,oI-FAoI, △9=FA,(T4-T)
• Blackbody Radiation Exchange i j i j i i q F A J → = , 4 J = Eb =σT j i j i j j q F A J → = , If Ai &Aj are blackbody, no reflection, Net radiation heat transfer between the surfaces 4 , 4 ij Fi, j Ai Ti Fj iAj Tj Δq = σ − σ ( ) 4 4 ij Fi, j Ai Ti Tj Δq = −