
Lecture 14 Two methods to solve differential equation Jiangi Sun April 22
Lecture 14 : Two methods to solve differential equation Jianqi Sun April 22
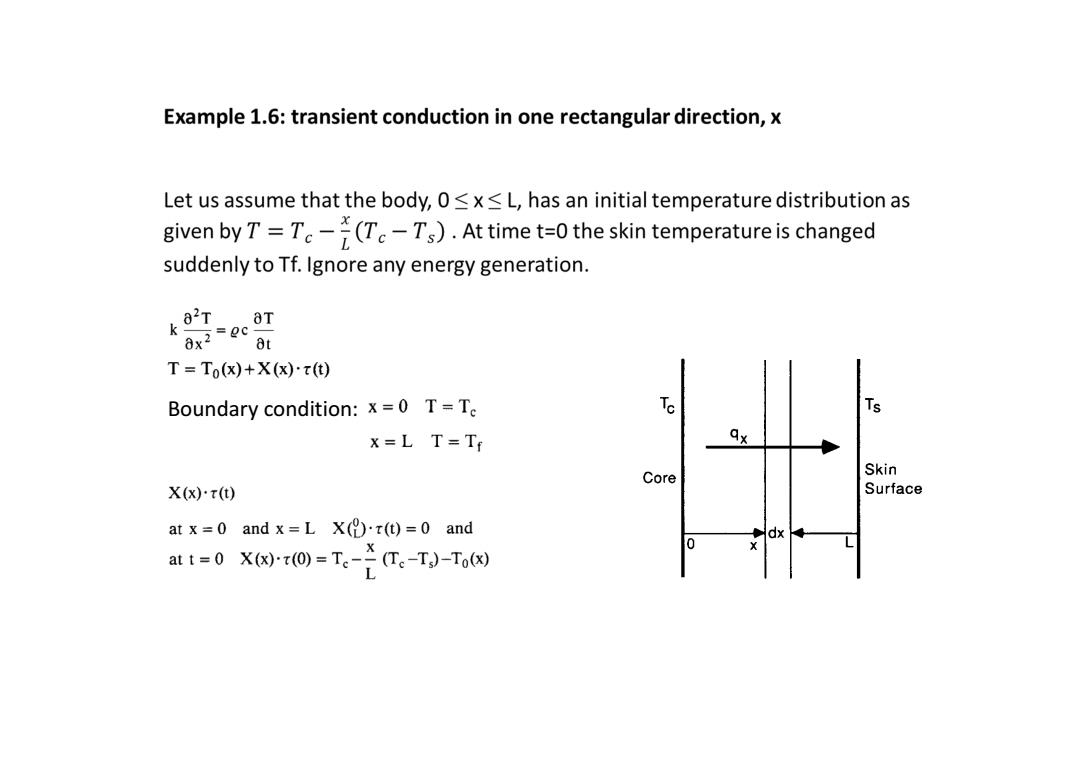
Example 1.6:transient conduction in one rectangular direction,x Let us assume that the body,0<x<L,has an initial temperature distribution as given byT=T(Tc-Ts).At time t=0 the skin temperature is changed suddenly to Tf.Ignore any energy generation. k OTT T=To(x)+X(x).t(t) Boundary condition:x=0 T=Te Ts x=L T=Tt Core Skin X(x)·T(t) Surface at x=0 and x=L X().r(t)=0 and dx at=0X侧r0=-i便.-T-ToW
Boundary condition:

Example: Problem Statement: One person is swimming outside in winter. The water temperature is assumed the same as that of the ambient (about 5C).Estimate the body temperature distribution with respect to time
Example: Problem Statement: One person is swimming outside in winter. The water temperature is assumed the same as that of the ambient (about 5oC). Estimate the body temperature distribution with respect to time

Problem Analysis and Assumptions 。1-D Approximation Metabolic Activity Negligible (prior to activity) Uniform Effective Thermal Conductivity (Blood Tissue)to be 0.5 W/K/m .Uniform pCp=3.6*106 J/K/m3
Problem Analysis and Assumptions • 1-D Approximation • Metabolic Activity Negligible (prior to activity) • Uniform Effective Thermal Conductivity (Blood + Tissue) to be 0.5 W/K/m • Uniform = 3.6*10 6 J/K/m 3 p ρc
L Body,K X
Body, k L/2 Tw Body, k L/2 Tw L b T ∞ h

Solution Governing Equation: PCp t (1a) Boundary Condition: x=0, OT-h(T-T.) d (1b) x=L, T=T,=310K Initial Condition: t=0,T=T,=310K (1c)
Solution ( ) p T T c k txx ρ ∂ ∂∂ = ∂∂ ∂ 0, ( ) , 310 b T x k hT T x xL TT K ∞ ∂ = =− ∂ = == Governing Equation: Boundary Condition: Initial Condition: (1a) (1b) (1c) 0, 310 b t TT K = ==

Continued Separating T(x,t)to T(x,t)=θ(x,t)+T The equations change to (1a) ∂0 x=0, x ≥hd (1b) x=L, 0=T6-T=32K t=0, 0=T-T=32K (1c)
Continued ( ) p c k txx θ θ ρ ∂ ∂∂ = ∂∂ ∂ 0, , 32 b x kh x x L TT K θ θ θ ∞ ∂ = = ∂ = =− = T xt xt T (,) (,) = + θ ∞ The equations change to : (1a) (1b) (1c) Separating T(x,t) to 0, 32 b t TT K = =− = θ ∞

Continued General Solution Particular Solution: e(x,t)=T,(x,t)+T (x)
Continued General Solution + Particular Solution: (,) (,) () n w θ x t T xt T x = +

For the particular Solution T.) k)=0 Ox Ox x=0, OT=hTw k Ox x=L, Tn=T6-T。 T (x)=cx+c2 h(T-T) k(T-T.) C= k+hl C2= k+hl
( ) = 0 ∂∂ ∂∂ xT k x w 0, , w w w b T x k hT x xL T TT∞ ∂ = = ∂ = =− 1 2 ( ) T x cx c w = + For the particular Solution ( ) T x w 1 ( ) b hT T c k hL − ∞ = + ( ) 2 b kT T c k hL − ∞ = +

General Solution T (x,t) r, OT,(x,t)d pcp Ox x=0, T,=0 x=L, T,=0 t=0, Tn=Tb-T。-T
General Solution (,) (,) ( ) n n p T xt T xt c k txx ρ ∂ ∂ ∂ = ∂∂ ∂ 0, 0 , 0 n n x T xL T = = = = 0, nb w t T TT T = =−− ∞ (,) T xt n