ME369 Modeling,Analysis and System Control-A --Lecture 141112 Week 9# Nov.10(M) Frequency-Introduction,Response Ch7.1 HW4 due Nov.12(W) Frequency-Nyquist Plot Ch7.3 HW5 Week 10# Nov.17(M) Midterm Exam Nov.19(W) Frequency-Bode Diagram Ch7.2
ME369 Modeling, Analysis and System Control-A --Lecture_141112 Week 9# Nov.10(M) Frequency-Introduction, Response Ch7.1 Nov.12(W) Frequency-Nyquist Plot Ch7.3 HW4 due HW5 Week 10# Nov.17(M) Midterm Exam Nov.19(W) Frequency-Bode Diagram Ch7.2

Midterm Exam announcement ·Date:Now.17(M① Time:7:50~9:50 120 minutes ·Place:Education Building D-502(东上院) One piece ofA4 paper is allowed, must be hand written
Midterm Exam announcement • Date: Nov. 17 (M) • Time: 7:50~9:50 , 120 minutes • Place: Education Building D-502 ( 东上院 ) • One piece of A4 paper is allowed, must be hand written

Problems of HW5 ·Refer to the ftp site. ftp://public.sjtu.edu.cn ·User:yuanjj ·Password:public DUE:Dec.3(W)
Problems of HW5 • Refer to the ftp site. • ftp://public.sjtu.edu.cn • User: yuanjj • Password: public DUE: Dec.3(W)

The Nyquist Plots(Polar plots) [Polar Plot]:the Nyquist plot of a sinusoidal transfer function G(j@) is a plot of the magnitude versus the phase angle in polar coordinates as w is varied from 0 to oo. Im Im U(一 0 Re 0 Re p() p(ol) A(j) p(2) A(⊙1) G(j 2) G0)
[Polar Plot]: the Nyquist plot of a sinusoidal transfer function G( j ) is a plot of the magnitude versus the phase angle in polar coordinates as w is varied from 0 to ∞. The Nyquist Plots (Polar plots)

112 Draw the Nyquist plot of a control system G(S)= s(1+0.02s) 112 G(j0)=G©)(1+0.02j0) -112×0.02 2-j0.4×100+0 112 =2 -1 0.4×10803+ o=100 可 a=80f C U(@) (c) -1 00 20 -1.93 =4.89 ⊙=40 30 2 -1.64 -2.75 General procedure: 0=30 1.Derive the sinusoidal TF G@ofthe system; 2.Find the value G(@when@=0,ando=oo; Key notes: 3.Derive the intersection of G(@)with two axes; @=0,@=oo,Direction 4.Plot extra mid-points if necessary; 5.Link the approximate curves
Draw the Nyquist plot of a control system Key notes: = 0, = , Direction General procedure: 1. Derive the sinusoidal TF G(j ) of the system; 2. Find the value G(j ) when= 0, and = ; 3.Derive the intersection of G(j ) with two axes; 4. Plot extra mid-points if necessary; 5. Link the approximate curves. ( 1 0.02 ) 112 ( ) s s G s

Basic factors of the Control System K(红,s+1)(s+25s+)u+2n=m G(S)= 1=1 k=1 ,n≥m sΠ(T,s+1)Π(Ts2+25,Ts+ )(w+p+2o=n i=l j=1 Gain K(放大环节) First-order factor(惯性环节) K(joT,+1o)t+25(j@)+1D G(j0)= 1=1 k=1 (jo)(joT,+DIHi@)T+24,T(jo)+1 i=1 j=1 Integral factor 1/jo(积分环节) Quadratic factors(振荡环节)
Basic factors of the Control System 1 1 2 2 1 1 2 2 ( ) ( 1 ) [( ) 2 ( ) 1 ] ( 1 ) [( ) 2 ( ) 1 ] ( ) i j i j j j l k l k k k j j T j T T j K j j j G j Integral factor 1/j 积分环节 Gain K (放大环节 ) First-order factor (惯性环节 ) Quadratic factors (振荡环节 ) 2 2 1 1 2 2 1 1 ( 1) ( 2 1) 2 () ; ; 2 ( 1) ( 2 1) l k kk l k i j jj i j Ks s s m Gs n m n s Ts T s T s

Basic factors of the Control System Gain K(放大环节) Integral factor1jo(积分环节) ·Derivative factor jo(纯微分环节) ·First-order factor1/(1+joT)(惯性环节) First-order factor(1+joT)(一阶微分环节) 1 Quadratic factors (T2(o)2+2sT0o)+1) (振荡环节) Quadratic factors (T2(jo)2+2sT0o)+1) (二阶微分环节)
Basic factors of the Control System • Gain K (放大环节 ) • Integral factor 1/j 积分环节 • Derivative factor j 纯微分环节 • First-order factor 1/(1+j) (惯性环节 ) • First-order factor (1+j) (一阶微分环节 ) • Quadratic factors (振荡环节 ) • Quadratic factors ( ( ) 2 ( ( ) 1 ) 二阶微分环节 ) 2 2 T j T j ( ( ) 2 ( ) 1 ) 1 2 2 T j T j

Basic factors of G(j)H(jo) ·Gain K(放大环节) G(jO)=K 1G(j@)=VU2(@)+V2(@o)=K G(jo)- Im U(o) K 0 K Re
Basic factors of G(j )H(j ) • Gain K (放大环节 ) G ( j ) K | G ( j ) | U ( ) V ( ) K 2 2 0 K 0 tg U ( ) V ( ) G ( j ) tg 1 1
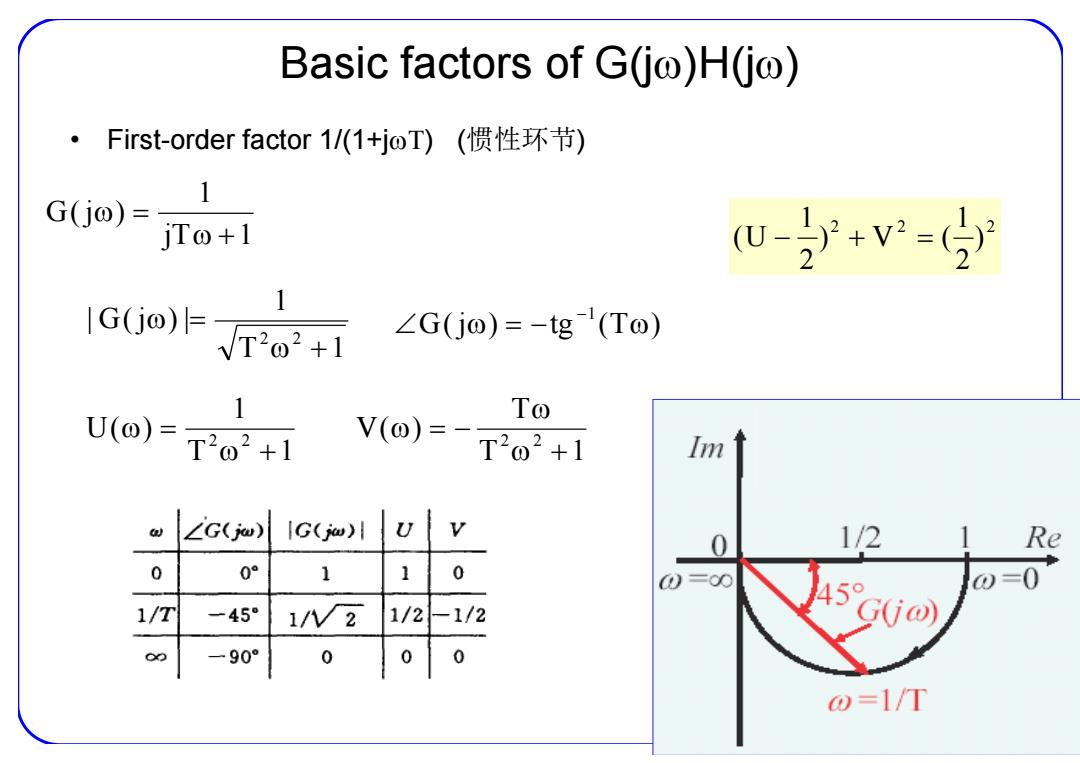
Basic factors of G(jo)H(jo) ·First-order factor1/(1+joT)(惯性环节) 1 G(j@)= jTo+l w-+v=分 lG(j@)E T2o2+1 ∠G(jo)=-g(To) 1 To U(0)= T202+1 V(o)=- T2o2+1 Im ∠G(jw) 1G()l U 0 1/21 Re 0 0° 1 1 0 0=00 0=0 1/T -45° 1/V2 1/2 -1/2 G(@ 一90° 0 0 o=1/T
Basic factors of G(j )H(j ) • First-order factor 1/(1+j) (惯性环节 ) jT 1 1 G ( j ) G ( j ) tg ( T ) 1 T 1 1 | G ( j ) | 2 2 T 1 1 U ( ) 2 2 T 1 T V ( ) 2 2 2 2 2 ) 2 1 ) V ( 2 1 ( U

Basic factors of G(jo)H(jo) ·Integral factor1/jo(积分环节) ∠G(jw)lG(w)iU(u) V(ω) 0 -90° 00 0 G0)-1。 -90° 1 0 -1 -90° 0 0 0 Im↑ 0=00 1 0 Re ∠G(jo)=tg1 =-90° 0 0=0
Basic factors of G(j )H(j ) • Integral factor 1/j 积分环节 1 j j 1 G ( j ) 90 0 1 G ( j ) tg 1 1 | G ( j ) |