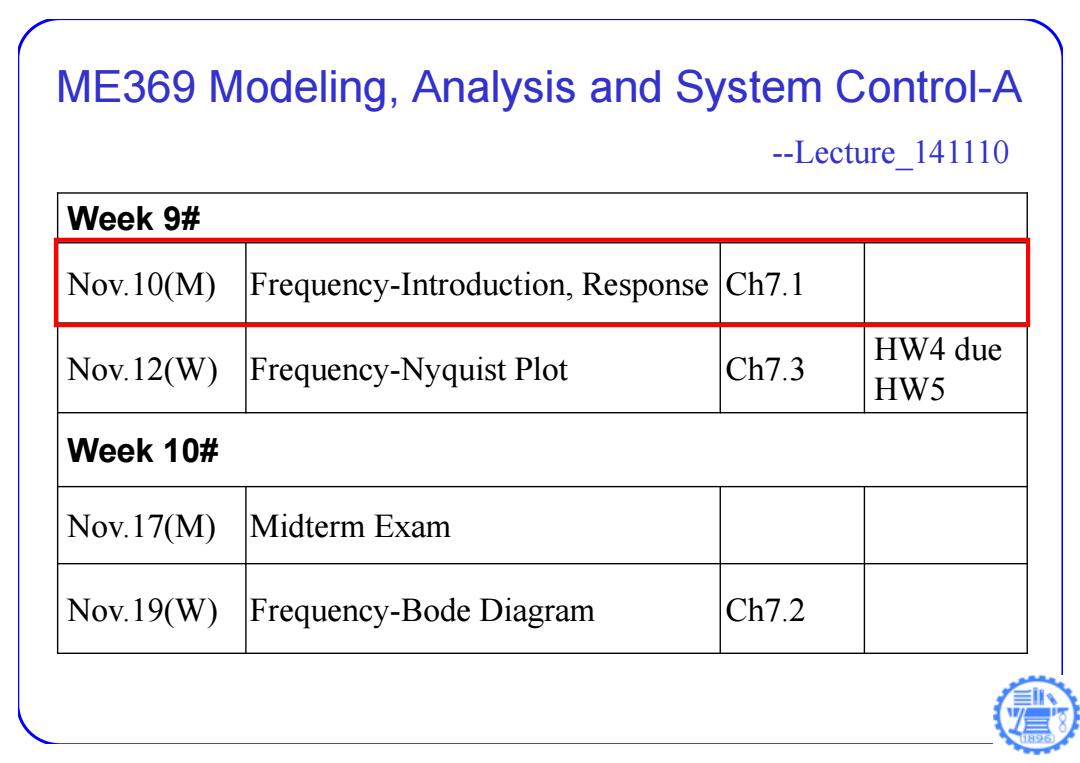
ME369 Modeling,Analysis and System Control-A --Lecture 141110 Week 9# Nov.10(M) Frequency-Introduction,Response Ch7.1 HW4 due Nov.12(W) Frequency-Nyquist Plot Ch7.3 HW5 Week 10# Nov.17(M) Midterm Exam Nov.19(W) Frequency-Bode Diagram Ch7.2
ME369 Modeling, Analysis and System Control-A --Lecture_141110 Week 9# Nov.10(M) Frequency-Introduction, Response Ch7.1 Nov.12(W) Frequency-Nyquist Plot Ch7.3 HW4 due HW5 Week 10# Nov.17(M) Midterm Exam Nov.19(W) Frequency-Bode Diagram Ch7.2

Midterm Exam announcement ·Date:Now.17(M① Time:7:50~9:50 120 minutes ·Place:Education Building D-502(东上院) One piece ofA4 paper is allowed, must be hand written
Midterm Exam announcement • Date: Nov. 17 (M) • Time: 7:50~9:50 , 120 minutes • Place: Education Building D-502 ( 东上院 ) • One piece of A4 paper is allowed, must be hand written
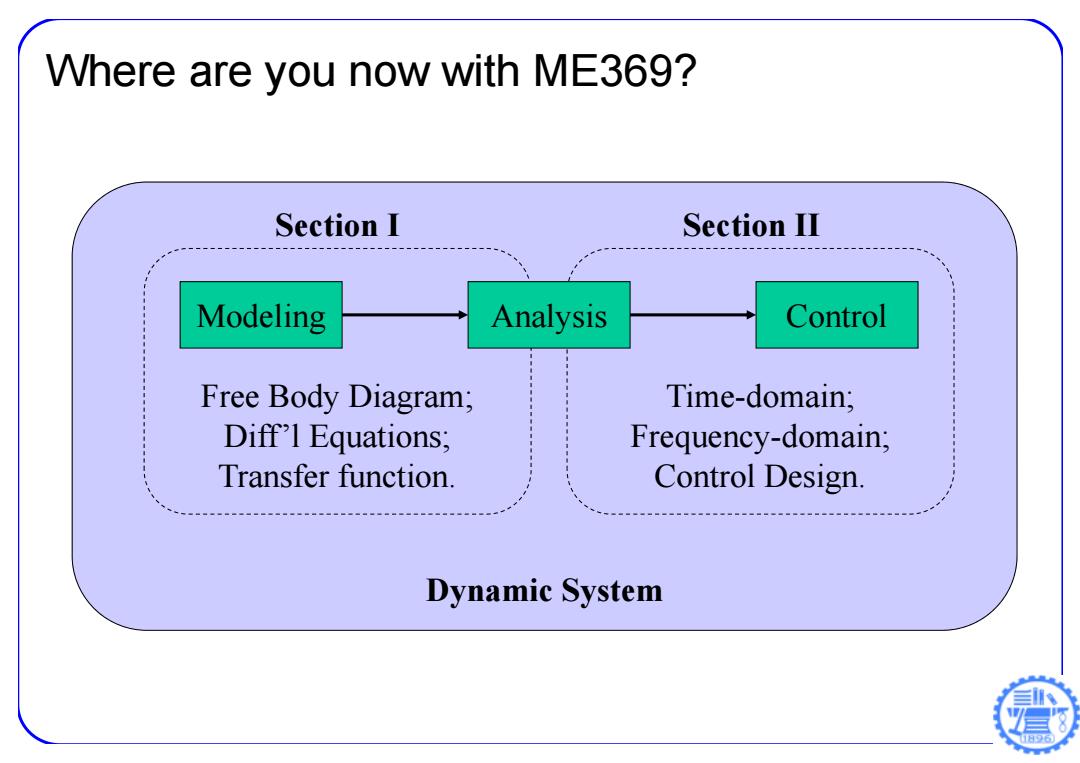
Where are you now with ME369? Section I Section II Modeling Analysis Control Free Body Diagram; Time-domain; Diff'l Equations; Frequency-domain; Transfer function. Control Design Dynamic System 日96
Modeling Control Dynamic System Free Body Diagram; Diff’l Equations; Transfer function. Time-domain; Frequency-domain; Control Design. Analysis Section I Section II Where are you now with ME369?
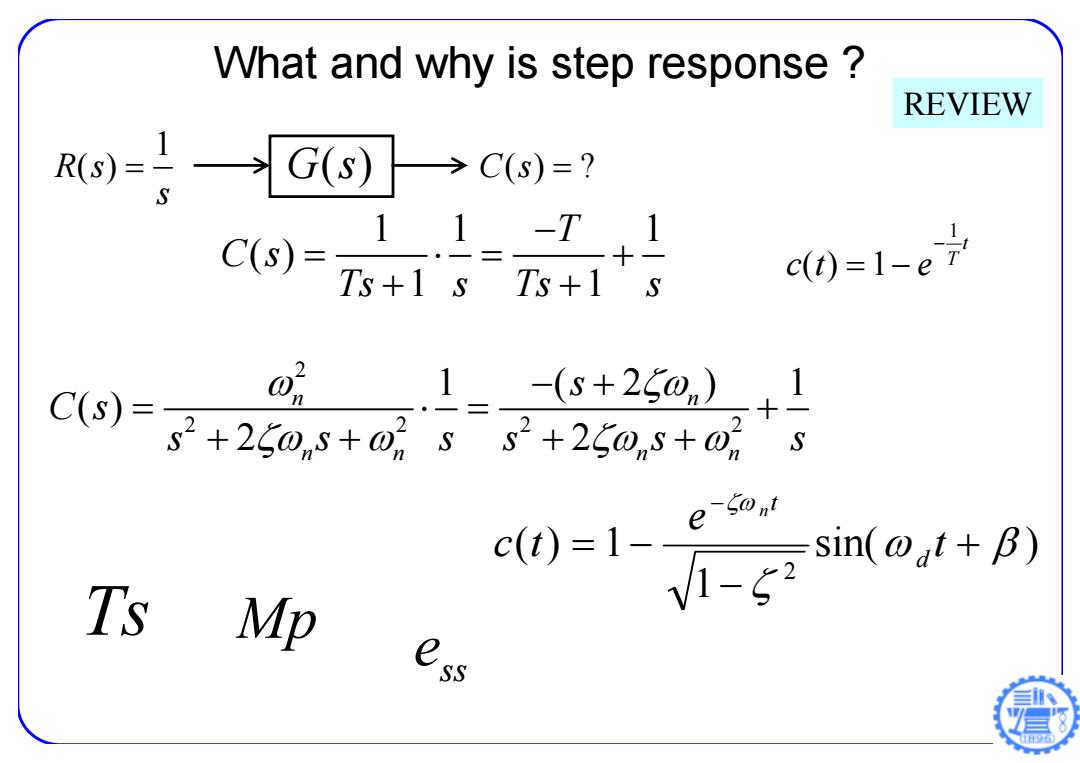
What and why is step response REVIEW Rd)=。 G(s)→ C(s)=? 11-T,1 C(S)= 十一 Ts+1 s Ts+1 s c0=1-e7 1_-(s+250n),1 C(s)=g+260,5+0ss+25@s+@ 十一 S e Ts Mp )in(ed+) s
What and why is step response ? 11 1 ( ) 1 1 T C s Ts s Ts s 1 () 1 t T ct e REVIEW 1 R s( ) s G s( ) C s() ? 2 2 22 2 1 (2 ) 1 ( ) 2 2 n n nn nn s C s s s ss s s sin( ) 1 ( ) 1 2 t e c t d t n Ts Mp s s e
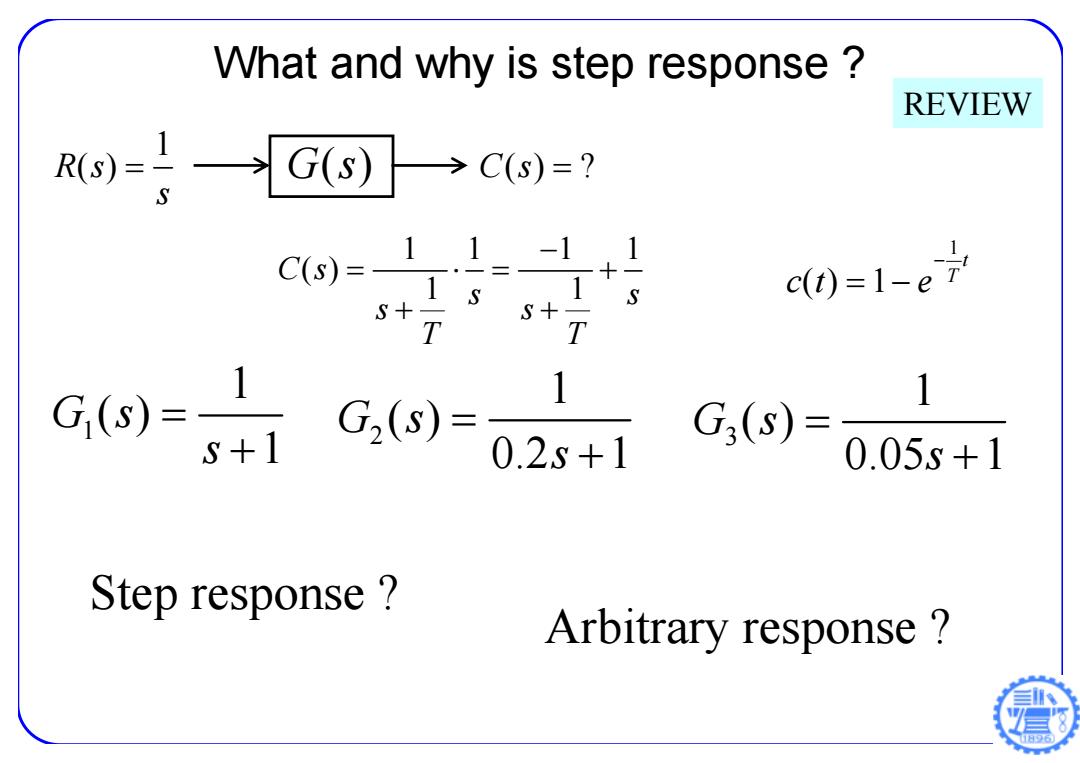
What and why is step response REVIEW R9 G(s→Cs)=? C(= 1 1-1 1 1 s+ S c0=1-e7 S+ T 1 C,(025 1 0.05s+1 Step response? Arbitrary response?
What and why is step response ? 11 11 ( ) 1 1 C s s s s s T T 1 () 1 t T ct e REVIEW 1 R s( ) s G s( ) C s() ? 1 1 ( ) 1 G s s 2 1 ( ) 0.2 1 G s s 3 1 ( ) 0.05 1 G s s Step response ? Arbitrary response ?

What and why is step response REVIEW 9片 GSC()=? 1 -(s+250n).1 C(s)=g+26@,s+ag^ss2+25@,s+o 十 e -50nt 20 G(s)= 2+4s+20 )sin() 32 G,(s)=g+8s+32 80 Step response G,(s)=g+8s+80 Arbitrary response ?
What and why is step response ? REVIEW 1 R s( ) s G s( ) C s() ? 1 2 20 ( ) 4 20 G s s s Step response ? Arbitrary response ? 2 2 22 2 1 (2 ) 1 ( ) 2 2 n n nn nn s C s s s ss s s sin( ) 1 ( ) 1 2 t e c t d t n 2 2 32 ( ) 8 32 G s s s 3 2 80 ( ) 8 80 G s s s

Transient frequency response C(s) =Gs)= 1 if r(t)=sinot,what is c(t)? R(s) Ts+1 1 a C(s)= bs+c Ts+1s2+02-Ts+ 1s2+02 1+07,b=07 @T2 a= 1+07,c=1+7 c(1)-e+bcost+sinot a T c(t)= a Msin(t -e ba -arctg -arctgaT Steady-state response Goes to zero in steady-state 日96
Transient frequency response Goes to zero in steady-state Steady-state response 1 1 ( ) ( ) ( ) Ts G s R s C s if r ( t ) sin t, what is c ( t ) ? 2 2 2 2 1 1 1 ( ) s bs c Ts a Ts s C s 1 ( ) cos sin t T a c ct e b t t T 2 2 2 2 2 2 2 1 , 1 , 1 T c T T b T T a 1 ( ) sin( ) t T a ct e M t T arctg T c b arctg T c M b 2 2 2 2 2 1 1

Electronic examples M=2 2 R(s) 4=arcg°-acgo2 c0=ue宁+Msin(aw+) Low-pass filter High-pass filter Band-pass filter 日96
Electronic examples Low-pass filter High-pass filter Band-pass filter ( ) sin( ) 1 c t ae M t t T 1 1 ( ) ( ) ( ) Ts G s R s C s arctg T c b arctg T c M b 2 2 2 2 2 1 1

Response of Exponential Functions For a physical system described by the transfer function G(s),when the input signal [assumed to be slow compared to the dynamics of G(s)]is in the form (t)=e",then the output signal (under zero initial conditions)will also be exponential. y(t)=g()u(t-t)dr=g(r)edr=g(r)e-dr.e" =G(s)e Convolution Integral Theorem:L[()g(-)d]=F(s)G(s)
Response of Exponential Functions • For a physical system described by the transfer function G(s), when the input signal [assumed to be slow compared to the dynamics of G(s)] is in the form , then the output signal (under zero initial conditions) will also be exponential. u ( t ) e s1 t 1 11 1 ( ) 0 00 1 () ( ) ( ) ( ) ( ) ( ) s t s st s t y t g ut d g e d g ede Gs e Convolution Integral Theorem: [ ( ) ( ) ] ( ) ( ) 0 L f g t d F s G s t

Im t I=ej@t Re Euler's formula e=cos中+jsin 日96
cos sin j e j Euler’s formula