
第一章测量及测量系统基础 1-1测量的定义是什么?测量结果表示包含哪些内容? 解:测量:通过使用一个经过标准单位标定的仪器或设备,或者通过与一个 已知规模大小的物体相比较来确定大小、数量或程度。 测量结果表示为测量对象的真值替代值加上各类测量误差的算术和。 x=元士u单位 u 4,=元×100% 式中为多次测量的平均值,u为合成不确定度,为相对不确定度。 1-2用框图来表示现代数字化测量系统的基本构成?每个环节的作用分别是什 么? 解:现代数字化测量系统的基本构成: 传 计 研究 调理 数据 感 采集 算 对象 器 电路 器 机 1.传感器:将物理量转化为电信号。 2. 调理电路:将传感器输出的电信号调理为适合数据采集器的电压输入。 3. 数据采集器一一将代表输入信号的电压离散采样后输入计算机。 4.计算机一一计算机将由采集器输入的信号通过软件进行分析处理之后, 分析结果显示在其屏幕上或存储在指定介质上。 1-3直接测量方法和间接测量方法有何不同? 解:直接测量法:用预先按标准量标定好的仪器对被测量进行测量或用标准 量直接与被测量进行比较,从而从仪器的指示机构的读数直接获得被测量的 值得一种测量方法;间接测量:通过对与被测量有函数关系的其他量的测量 而通过计算得到被测量值的测量方法。与直接测量法相比,间接测量一般测 量过程复杂费时,手续繁多,花费时间相对较长,引起误差的因素也较多。 1-4什么是测量系统的静态特性?表征测量系统静态特性的主要指标有哪些? 它们是如何定义的? 解:测量系统的静态特性是在静态测量情况下描述实际测量系统与理想线性 时不变系统的接近程度。 表征测量系统静态特性的主要指标有: 1.灵敏度:表征测量系统对输入信号变化的一种反应能力。党系统的输入x 有一个微小增量△x时,将引起系统的输出y也发生相应的微量变化△y, 定义该系统的灵敏度为S=△y/△x。 2.非线性度:指系统的输出/输入之间保持常值比例关系(线性关系)的一 种度量。在测量系统的标称输出范围(全量程)A内,标定曲线与该拟 合直线的最大偏差Bmax与A的比值,即非线性度=Bmax/AX100%。 3.回程误差:也称为滞差或滞后量,表征测量系统在全程范围内,输入递 增变化(由小变大)中的标定曲线和递减变化(由大变小)中的标定曲 线二者静态特征不一致的程度。在测量系统的全量程A范围内,不同输 出量中差值最大者(hmax=y2-yi)与全量程A之比,即回程误差=hmax/AX 100% 4.零位:当输入为零时测量系统的输出值,理想的线性测量系统中,零位应
第一章 测量及测量系统基础 1-1 测量的定义是什么?测量结果表示包含哪些内容? 解:测量:通过使用一个经过标准单位标定的仪器或设备,或者通过与一个 已知规模大小的物体相比较来确定大小、数量或程度。 测量结果表示为测量对象的真值替代值加上各类测量误差的算术和。 { 𝑥 = 𝑥̅± 𝑢单位 𝑢𝑟 = 𝑢 𝑥̅ × 100% 式中𝑥̅为多次测量的平均值,u 为合成不确定度,ur为相对不确定度。 1-2 用框图来表示现代数字化测量系统的基本构成?每个环节的作用分别是什 么? 解:现代数字化测量系统的基本构成: 1. 传感器:将物理量转化为电信号。 2. 调理电路:将传感器输出的电信号调理为适合数据采集器的电压输入。 3. 数据采集器——将代表输入信号的电压离散采样后输入计算机。 4. 计算机——计算机将由采集器输入的信号通过软件进行分析处理之后, 分析结果显示在其屏幕上或存储在指定介质上。 1-3 直接测量方法和间接测量方法有何不同? 解:直接测量法:用预先按标准量标定好的仪器对被测量进行测量或用标准 量直接与被测量进行比较,从而从仪器的指示机构的读数直接获得被测量的 值得一种测量方法;间接测量:通过对与被测量有函数关系的其他量的测量 而通过计算得到被测量值的测量方法。与直接测量法相比,间接测量一般测 量过程复杂费时,手续繁多,花费时间相对较长,引起误差的因素也较多。 1-4 什么是测量系统的静态特性?表征测量系统静态特性的主要指标有哪些? 它们是如何定义的? 解:测量系统的静态特性是在静态测量情况下描述实际测量系统与理想线性 时不变系统的接近程度。 表征测量系统静态特性的主要指标有: 1. 灵敏度:表征测量系统对输入信号变化的一种反应能力。党系统的输入 x 有一个微小增量∆x 时,将引起系统的输出 y 也发生相应的微量变化∆y, 定义该系统的灵敏度为 S=∆y/∆x。 2. 非线性度:指系统的输出/输入之间保持常值比例关系(线性关系)的一 种度量。在测量系统的标称输出范围(全量程)A 内,标定曲线与该拟 合直线的最大偏差 Bmax 与 A 的比值,即非线性度=Bmax/A×100%。 3. 回程误差:也称为滞差或滞后量,表征测量系统在全程范围内,输入递 增变化(由小变大)中的标定曲线和递减变化(由大变小)中的标定曲 线二者静态特征不一致的程度。在测量系统的全量程 A 范围内,不同输 出量中差值最大者(hmax=y2i-y1i)与全量程 A 之比,即回程误差=hmax/A× 100% 4. 零位:当输入为零时测量系统的输出值,理想的线性测量系统中,零位应 计 算 机 数据 采集 器 调理 电路 传 感 器 研究 对象

该为零或是一个不随输入而改变的定值,但由于调离电路总是存在输入 失调,该值一般不会为零,且零位会随输入中共模分量大小变化俄变化。 5.分辨率或分辨力:数字化测量系统中特有,分辨力是指系统能分辨的最 小输入变化量,即1个LSB,一般等于, 分辨率是分辨力相对测量量 程的百分数,即1 2n1 1-5什么是测量系统的动态特性?表征测量系统动态特性的主要指标有哪些? 它们是如何定义的? 解:测量系统的动态特性是指输入量随时间快速变化时,系统的输出随输入 而变化的关系。 动态性能指标: 1.时域动态性能指标 (一)一阶系统 ①时间常数T:输出量上升到稳态值的63.2%所需要的时间。 ②响应时间ts:输出量达到稳态值的某一允许误差范围内,并保 持在此范围内所需的最小时间。 ③上升时间t:测量设备输出响应值从5%(或10%)到稳态值 的95%(或90%),或从0上升到稳态值所需的时间。 ④延迟时间t:测量设备输出响应值从0上升到稳态值的50%所 需的时间。 (二)二阶系统 ①峰值时间t:输出响应曲线达到第一个峰值所需时间。 ②超调量M,:输出响应曲线的最大偏差与稳态值的百分比。 ③上升时间t:t,=-E=-arccos< d ωnV1-z ④衰减比6:表示过度过程曲线时间相差一个周期T的两个峰值 之比,即8=an/an+2 4 当=0.02 ⑤调整时间t:ts= ωn 3 当△=0.05 n 2.频域动态性能指标 ①频带宽ωb:对数幅频特性曲线上幅值增益不超过±ndB(如±3dB,n=3) 所对应的频率范围。 ②工作频带(0~wg):与给定的测量系统幅值误差范围(如±1%,±2%) 相对应的频率范围。 ③跟随角b:当ω=ωb时,对应相频特性上的相角。 1-6一阶系统的传递函数是什么?一阶系统的幅频特性和相频特性曲线的特征 有哪些? 解:一阶系统的传递函数为: Y(s)k H(S)= X(S)-S+1 一阶系统频率特性的特点:
该为零或是一个不随输入而改变的定值,但由于调离电路总是存在输入 失调,该值一般不会为零,且零位会随输入中共模分量大小变化俄变化。 5. 分辨率或分辨力:数字化测量系统中特有,分辨力是指系统能分辨的最 小输入变化量,即 1 个 LSB,一般等于𝑉𝑟𝑒𝑓 2 𝑛−1,分辨率是分辨力相对测量量 程的百分数,即 1 2 𝑛−1。 1-5 什么是测量系统的动态特性?表征测量系统动态特性的主要指标有哪些? 它们是如何定义的? 解:测量系统的动态特性是指输入量随时间快速变化时,系统的输出随输入 而变化的关系。 动态性能指标: 1. 时域动态性能指标 (一)一阶系统 ①时间常数 T:输出量上升到稳态值的 63.2%所需要的时间。 ②响应时间 ts:输出量达到稳态值的某一允许误差范围内,并保 持在此范围内所需的最小时间。 ③上升时间 tr:测量设备输出响应值从 5%(或 10%)到稳态值 的 95%(或 90%),或从 0 上升到稳态值所需的时间。 ④延迟时间 td:测量设备输出响应值从 0 上升到稳态值的 50%所 需的时间。 (二)二阶系统 ①峰值时间 tp:输出响应曲线达到第一个峰值所需时间。 ②超调量 Mp:输出响应曲线的最大偏差与稳态值的百分比。 ③上升时间 tr:𝑡𝑟 = 𝜋−𝛽 𝜔𝑑 = 𝜋−𝑎𝑟𝑐𝑐𝑜𝑠𝜁 𝜔𝑛√1−𝜁 2 ④衰减比δ:表示过度过程曲线时间相差一个周期 T 的两个峰值 之比,即δ = 𝑎𝑛/𝑎𝑛+2 ⑤调整时间 ts:t𝑠 = { 4 𝜁𝜔𝑛 ,当∆= 0.02 3 𝜁𝜔𝑛 ,当∆= 0.05 2. 频域动态性能指标 ①频带宽ω𝑏:对数幅频特性曲线上幅值增益不超过±ndB(如±3dB,n=3) 所对应的频率范围。 ②工作频带(0~𝜔𝑔):与给定的测量系统幅值误差范围(如±1%, ± 2%) 相对应的频率范围。 ③跟随角𝜃𝑏:当ω = 𝜔𝑏时,对应相频特性上的相角。 1-6 一阶系统的传递函数是什么?一阶系统的幅频特性和相频特性曲线的特征 有哪些? 解:一阶系统的传递函数为: H(s) = 𝑌(𝑠) 𝑋(𝑠) = 𝑘 𝜏𝑠 + 1 一阶系统频率特性的特点:

①一阶系统是一个低通环节。只有当ω远小于1/时,幅频响应才接近于1, 因此一阶系统只适用于被测量缓慢或低频的参数。 ②ω=1幅频特性降为原来的0.707(即-3dB),相位角滞后45°,时间常数x 决定了测量系统适应的工作频率范围。 ③时间常数τ越小,频率响应特性较好。 ④当ωt《1时,k(ω)≈1,p(ω)=-45°,表明系统输出与输入为线性关系, 相位差与频率ω呈线性关系,输出yt)比较真实地反映输入xt)的变化规 律。 1-7一阶系统的时间常数是如何定义的? 解:输出量上升到稳态值的63.2%所需要的时间。 1-8测量系统的动态误差是什么? 解:当测量系统输入时随时间变化的动态信号xt)时,其相应的输出yt)或 多或少总是与xt)不一致,两者之间的差异即为动态误差。 1-9影响二阶系统动态特性的参数有哪些?对系统有何意义? 解:ζ、ωo对系统的意义体现在: ①二阶系统是一个振荡环节,当输入信号的频率ω等于测量装置的固有频 率,即ω=on处是装置的共振点。A(ω)=1/2ξ,所以阻尼比(很小时, 将产生很高的共振峰。 ②二阶系统是一个低通环节,曲线呈水平状态,随ω的增大,A(ω)先进入 共振区,后进入衰减区。 ③当=0.7左右时,A(o)几乎无共振,其水平段最长,其相频特性几乎是 一斜直线。 1-10用一时间常数为2s的温度计测量炉温时,当炉温在200~400℃之间,按正 弦规律变化时,周期为150s,温度计输出的变化范围是多少? 解:已知条件: x(t)=300+100sinωt 2π2π 0= T=150 t=2s 温度计为一阶系统,其幅频特性为 1 1 A(ω)= ==0.9930 V(wT)2+1 V50×2)2+1 2π 输入为200℃、400℃时,其输出为: y=300-A(o)×100=200.7(℃) y=300+A(ω)×100=399.3(°C) 1-11用一个一阶系统对100Hz正弦信号输入信号进行测量,如要求限制振幅误差 在5%以内,那么时间常数应取为多少?若用该系统测量50Hz正弦信号,问 此时的振幅误差和相角差是多少? 解:一阶系统的幅频特性
①一阶系统是一个低通环节。只有当ω远小于1/τ时,幅频响应才接近于 1, 因此一阶系统只适用于被测量缓慢或低频的参数。 ②ω = 1 𝜏幅频特性降为原来的 0.707(即-3dB),相位角滞后 45°,时间常数𝜏 决定了测量系统适应的工作频率范围。 ③时间常数𝜏越小,频率响应特性较好。 ④当ω𝜏 ≪ 1时,k(ω) ≈ 1, φ(ω) = −45°,表明系统输出与输入为线性关系, 相位差与频率ω呈线性关系,输出 y(t)比较真实地反映输入 x(t)的变化规 律。 1-7 一阶系统的时间常数是如何定义的? 解:输出量上升到稳态值的 63.2%所需要的时间。 1-8 测量系统的动态误差是什么? 解:当测量系统输入时随时间变化的动态信号 x(t)时,其相应的输出 y(t)或 多或少总是与 x(t)不一致,两者之间的差异即为动态误差。 1-9 影响二阶系统动态特性的参数有哪些?对系统有何意义? 解:ζ、𝜔0 对系统的意义体现在: ①二阶系统是一个振荡环节,当输入信号的频率ω等于测量装置的固有频 率,即ω = ω𝑛处是装置的共振点。A(ω) = 1/2ξ,所以阻尼比ζ很小时, 将产生很高的共振峰。 ②二阶系统是一个低通环节,曲线呈水平状态,随ω的增大,A(ω)先进入 共振区,后进入衰减区。 ③当ξ = 0.7左右时,A(ω)几乎无共振,其水平段最长,其相频特性几乎是 一斜直线。 1-10用一时间常数为 2s 的温度计测量炉温时,当炉温在 200~400℃之间,按正 弦规律变化时,周期为 150s,温度计输出的变化范围是多少? 解:已知条件: x(t) = 300 + 100sinω𝑡 ω = 2𝜋 𝑇 = 2𝜋 150 τ = 2s 温度计为一阶系统,其幅频特性为 A(ω) = 1 √(𝜔𝜏) 2 + 1 = 1 √( 2𝜋 150 × 2) 2 + 1 = 0.9930 输入为 200℃、400℃时,其输出为: y = 300 − A(ω) × 100 = 200.7(℃) y = 300 + A(ω) × 100 = 399.3(℃) 1-11用一个一阶系统对 100Hz 正弦信号输入信号进行测量,如要求限制振幅误差 在 5%以内,那么时间常数应取为多少?若用该系统测量 50Hz 正弦信号,问 此时的振幅误差和相角差是多少? 解:一阶系统的幅频特性
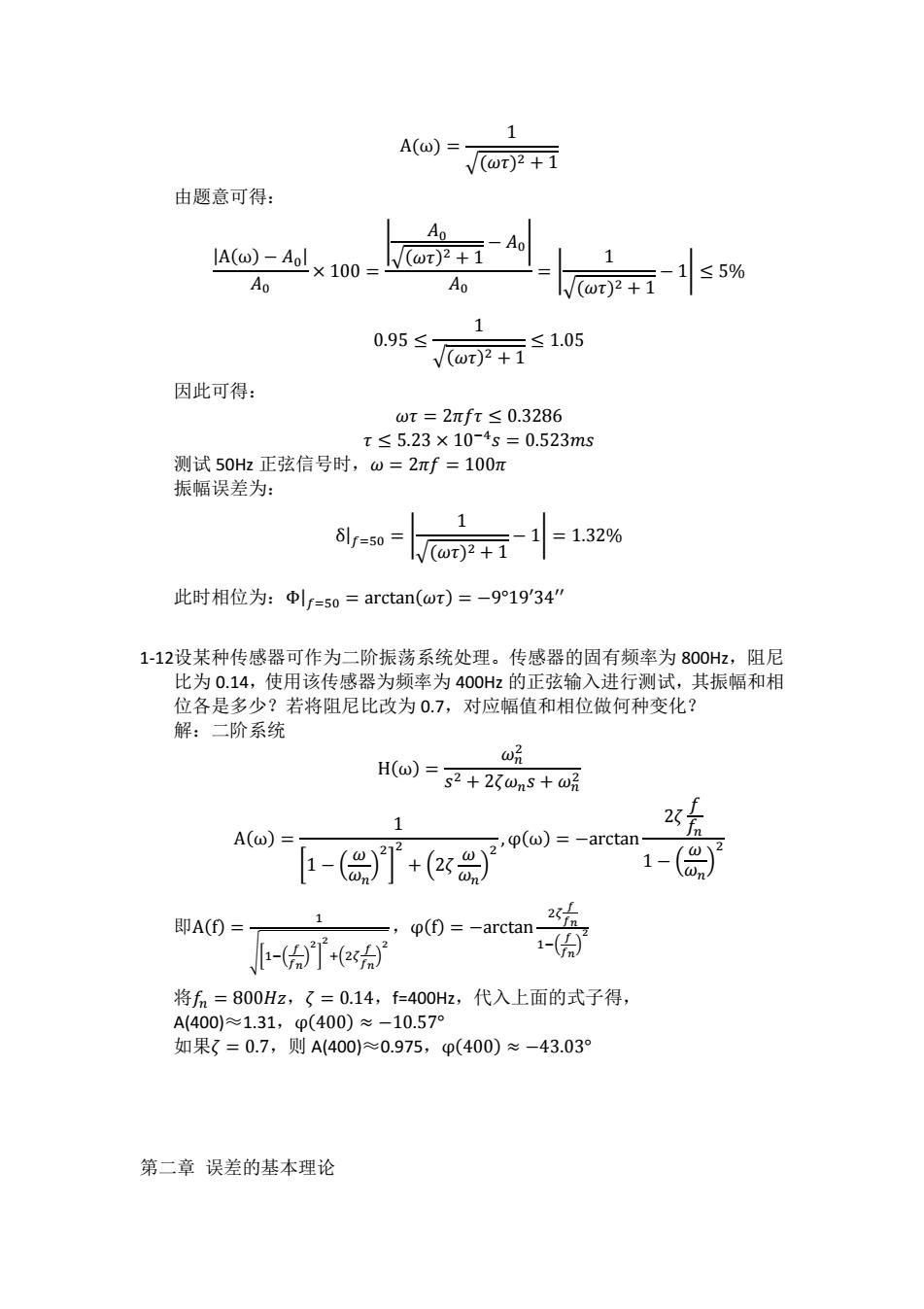
A(o)= V(wt)2+1 由题意可得: Ao -A0 IA()-Aol V(ω)2+1 ×100 Ao Ao wr)2+1 ≤5% 1 0.951 1.05 因此可得: wt=2πft≤0.3286 x≤5.23×10-4s=0.523ms 测试50Hz正弦信号时,w=2πf=100m 振幅误差为: 6lr=50= l(@t)2+1 1=1.32% 此时相位为:中ly=5o=arctan(wr)=-919'34" 1-12设某种传感器可作为二阶振荡系统处理。传感器的固有频率为800Hz,阻尼 比为0.14,使用该传感器为频率为400Hz的正弦输入进行测试,其振幅和相 位各是多少?若将阻尼比改为07,对应幅值和相位做何种变化? 解:二阶系统 ω晚 H(ω)= s2+2?wnS+ω2 1 2 A(ω)= p(w)=-arctan 1-() +(✉品) 1-( 即A()= (f)=-arctan -(T+s 1-( 将fn=800Hz,?=0.14,f=400Hz,代入上面的式子得, A(400)≈1.31,p(400)≈-10.57° 如果?=0.7,则A(400)≈0.975,φ(400)≈-43.03° 第二章误差的基本理论
A(ω) = 1 √(𝜔𝜏) 2 + 1 由题意可得: |A(ω) − 𝐴0 | 𝐴0 × 100 = | 𝐴0 √(𝜔𝜏) 2 + 1 − 𝐴0| 𝐴0 = | 1 √(𝜔𝜏) 2 + 1 − 1| ≤ 5% 0.95 ≤ 1 √(𝜔𝜏) 2 + 1 ≤ 1.05 因此可得: 𝜔𝜏 = 2𝜋𝑓𝜏 ≤ 0.3286 𝜏 ≤ 5.23 × 10−4 𝑠 = 0.523𝑚𝑠 测试 50Hz 正弦信号时,𝜔 = 2𝜋𝑓 = 100𝜋 振幅误差为: δ|𝑓=50 = | 1 √(𝜔𝜏) 2 + 1 − 1| = 1.32% 此时相位为:Φ|𝑓=50 = arctan(𝜔𝜏) = −9°19′34′′ 1-12设某种传感器可作为二阶振荡系统处理。传感器的固有频率为 800Hz,阻尼 比为 0.14,使用该传感器为频率为 400Hz 的正弦输入进行测试,其振幅和相 位各是多少?若将阻尼比改为 0.7,对应幅值和相位做何种变化? 解:二阶系统 H(ω) = 𝜔𝑛 2 𝑠 2 + 2𝜁𝜔𝑛𝑠 + 𝜔𝑛 2 A(ω) = 1 [1 − ( 𝜔 𝜔𝑛 ) 2 ] 2 + (2𝜁 𝜔 𝜔𝑛 ) 2 , φ(ω) = −arctan 2𝜁 𝑓 𝑓𝑛 1 − ( 𝜔 𝜔𝑛 ) 2 即A(f) = 1 √[1−( 𝑓 𝑓𝑛 ) 2 ] 2 +(2𝜁 𝑓 𝑓𝑛 ) 2 ,φ(f) = −arctan 2𝜁 𝑓 𝑓𝑛 1−( 𝑓 𝑓𝑛 ) 2 将𝑓𝑛 = 800𝐻𝑧,𝜁 = 0.14,f=400Hz,代入上面的式子得, A(400)≈1.31,φ(400) ≈ −10.57° 如果𝜁 = 0.7,则 A(400)≈0.975,φ(400) ≈ −43.03° 第二章 误差的基本理论

2-1测量误差分哪几类?它们各有什么特点? 解:按误差的性质不同来分,可分为系统误差、随机误差和粗大误差。 其各自特点如下: 系统误差:在相同条件下,多次测量同一量值时,该误差的绝对值和符号保 持不变,或者在条件改变时,按某一确定规律变化的误差。 随机误差:测得值与在重复性条件下对同一被测量进行无限多次测量结果的 平均值之差。单次测量数据中的随机误差无规律,多次测量数据则服从统计 学规律 粗大误差:明显超出统计规律预期值的误差。 2-2误差的绝对值与绝对误差是否相同?为什么? 解:不同。误差的绝对值,表示给误差值取正数:绝对误差:测量值与真实 值之间的差值,即:绝对误差=测量值-真实值,其数值可正可负。 2-3试述随机误差的主要特性。 解:随机误差的主要特性:在相同测量条件下,多次测量同一量值时,绝对 值和符号以不可预定方式变化。 2-4试述服从正态分布的随机误差的特性。 解:单峰性,对称性,有界性,抵偿性。 2-5检定2.5级(即最大引用误差为2.5%)的全量程为100V的电压表,发现50V 刻度点的示值误差2V为最大误差,问该电表是否合格? 解:最大引用误差Ynmax=Dm匹×100% Am 得Yn.max=品×100%=2%<2.5% 所以该电表合格。 2-6检定一个1.5级100mA的电流表,发现在50mA处的误差最大,其值为1.4mA, 其他刻度处的误差均小于1.4mA,这块电流表是否合格? 解:根据题意,最大绝对误差Dmax≤1.4mA 最大引用误差Ynmax=m×100% Am 得Yrmax=总×100%=14%<15% 所以,这块电表合格。 2-7用量程为10A的电流表,测量实际值为8A的电流,若读数为8.1A,求测量 的绝对误差和相对误差。若所求得的绝对误差被视为最大绝对误差,该电流 表的准确度等级可定为哪一级? 解:绝对误差D=X-x=8A-8.1A=-0.1A 最大引用误差Yn.max=竺×100%=1.0%,1.0级 Am 2-8某功率表的准确度等级为0.5级,表的刻度共分为150个小格,问:(1)该 表测量时,可能产生的最大误差为多少格?(2)当读数为140格和40格时, 最大可能的相对误差为多大? 解:(1)该表测量时,可能产生的最大相对误差为±0.5%,最大绝对误差为 Dmax=Am×Yn,max=150×±0.5%=±0.75格
2-1 测量误差分哪几类?它们各有什么特点? 解:按误差的性质不同来分,可分为系统误差、随机误差和粗大误差。 其各自特点如下: 系统误差:在相同条件下,多次测量同一量值时,该误差的绝对值和符号保 持不变,或者在条件改变时,按某一确定规律变化的误差。 随机误差:测得值与在重复性条件下对同一被测量进行无限多次测量结果的 平均值之差。单次测量数据中的随机误差无规律,多次测量数据则服从统计 学规律. 粗大误差:明显超出统计规律预期值的误差。 2-2 误差的绝对值与绝对误差是否相同?为什么? 解:不同。误差的绝对值,表示给误差值取正数;绝对误差:测量值与真实 值之间的差值,即:绝对误差=测量值-真实值,其数值可正可负。 2-3 试述随机误差的主要特性。 解:随机误差的主要特性:在相同测量条件下,多次测量同一量值时,绝对 值和符号以不可预定方式变化。 2-4 试述服从正态分布的随机误差的特性。 解:单峰性,对称性,有界性,抵偿性。 2-5 检定 2.5 级(即最大引用误差为 2.5%)的全量程为 100V 的电压表,发现 50V 刻度点的示值误差 2V 为最大误差,问该电表是否合格? 解:最大引用误差γ𝑛,𝑚𝑎𝑥 = 𝐷𝑚𝑎𝑥 𝐴𝑚 × 100% 得γ𝑛,𝑚𝑎𝑥 = 2 100 × 100% = 2% < 2.5% 所以该电表合格。 2-6 检定一个1.5级100mA的电流表,发现在50mA处的误差最大,其值为1.4mA, 其他刻度处的误差均小于 1.4mA,这块电流表是否合格? 解:根据题意,最大绝对误差𝐷𝑚𝑎𝑥 ≤ 1.4𝑚𝐴 最大引用误差γ𝑛,𝑚𝑎𝑥 = 𝐷𝑚𝑎𝑥 𝐴𝑚 × 100% 得γ𝑛,𝑚𝑎𝑥 = 1.4 100 × 100% = 1.4% < 1.5% 所以,这块电表合格。 2-7 用量程为 10A 的电流表,测量实际值为 8A 的电流,若读数为 8.1A,求测量 的绝对误差和相对误差。若所求得的绝对误差被视为最大绝对误差,该电流 表的准确度等级可定为哪一级? 解:绝对误差 D=X-x=8A-8.1A=-0.1A 最大引用误差γ𝑛,𝑚𝑎𝑥 = 𝐷𝑚𝑎𝑥 𝐴𝑚 × 100%=1.0%,1.0 级 2-8 某功率表的准确度等级为 0.5 级,表的刻度共分为 150 个小格,问:(1)该 表测量时,可能产生的最大误差为多少格?(2)当读数为 140 格和 40 格时, 最大可能的相对误差为多大? 解:(1) 该表测量时,可能产生的最大相对误差为±0.5%,最大绝对误差为 𝐷𝑚𝑎𝑥 = 𝐴𝑚 × γ𝑛,𝑚𝑎𝑥 = 150 × ±0.5% = ±0.75 格

(2)当读数为140格时最大相对误差为 D±0.75 V二A =140 =±0.535% 当读书为40格时最大相对误差为 D±0.75 Y= Ax 40 =±1.875% 2-9进行下述计算,并给出适当的有效数字。 2.52×4.10×15.14 3.10×21.14×5.10 (1) 6.16×104 (2) 0.0001120 51.0×4.03×10 0.0324×8.1×2.12×102 (3) 2.512×0.002034 (4) 1.050 2.2856×2.51+5.42-1.8904×7.50×103 (5) 3.5462 解:(1)2.54×103 (2)2.90×105 (3)4.02 (4)53 (5)3.14 2-10测量某电路电流共5次,测得数据(单位为mA)为168.41、168.54、168.59、 168.40、168.50。试求算术平均值及其标准差、随机误差和平均误差。 解:(1)算术平均值 X1= 亏(168.41+168.54+168.59+168.40+168.50) i=1 =168.488(mm) (2)标准差 ∑驶1(x-x) =0.08 n-1 (3)随机误差 p≈3 1(x-x) =0.05 5-1 (4)平均误差 4 0≈ 1x-x) 5 5-1 =0.06 2-11在满足欧姆定律的电路中,电流I由关系式=E/R来计算,其中E是电路的 电动势,R是电阻。试求由E和R的相对误差fE和fR引起的电流I的相对 误差。 解:f=lfel+fRl 2-12反复测量某电压10次,得到下列数据,经整理,按大小顺序排列为(单位 为伏特):25.46、25.47、25.48、25.48、25.49、27.49、25.50、25.50、25.51、 25.53,试用狄克松准则判别其中是否存在粗大误差的测量值
(2)当读数为 140 格时最大相对误差为 γ = 𝐷 𝐴𝑥 = ±0.75 140 = ±0.535% 当读书为 40 格时最大相对误差为 γ = 𝐷 𝐴𝑥 = ±0.75 40 = ±1.875% 2-9 进行下述计算,并给出适当的有效数字。 (1) 4 2.52 4.10 15.14 6.16 10 (2) 3.10 21.14 5.10 0.0001120 (3) 4 51.0 4.03 10 2.512 0.002034 (4) 2 0.0324 8.1 2.12 10 1.050 (5) 3 2.2856 2.51 5.42 1.8904 7.50 10 3.5462 解:(1)2.54×10-3 (2)2.90×106 (3)4.02 (4)53 (5)3.14 2-10测量某电路电流共 5 次,测得数据(单位为 mA)为 168.41、168.54、168.59、 168.40、168.50。试求算术平均值及其标准差、随机误差和平均误差。 解:(1)算术平均值 𝑥̅= 1 𝑛 ∑𝑥𝑖 = 1 5 (168.41 + 168.54 + 168.59 + 168.40 + 168.50) 𝑛 𝑖=1 = 168.488(𝑚𝑚) (2)标准差 σ = √ ∑ (𝑥𝑖 − 𝑥̅) 𝑛 𝑖=1 𝑛 − 1 = 0.08 (3)随机误差 ρ ≈ 2 3 √ ∑ (𝑥𝑖 − 𝑥̅) 5 𝑖=1 5 − 1 = 0.05 (4)平均误差 θ ≈ 4 5 √ ∑ (𝑥𝑖 − 𝑥̅) 5 𝑖=1 5 − 1 = 0.06 2-11在满足欧姆定律的电路中,电流 I 由关系式 I= E/R 来计算,其中 E 是电路的 电动势,R 是电阻。试求由 E 和 R 的相对误差 fE 和 fR 引起的电流 I 的相对 误差。 解:fI=|fE|+|fR| 2-12反复测量某电压 10 次,得到下列数据,经整理,按大小顺序排列为(单位 为伏特):25.46、25.47、25.48、25.48、25.49、27.49、25.50、25.50、25.51、 25.53,试用狄克松准则判别其中是否存在粗大误差的测量值

解:按照狄克松准则,n=10时,按r11判别,若给定的置信概率为0.95,查 表2-4得 11=-xm-=25.53-25.51_2 25.53-25.47=6 ≈0.333 X(n)-X(2) h1=x-x=25.47-25.46 x(m-1)-x1)25.51-25.46 0.2 因为r11、11都小于0.477,故判定此10次测量值不含粗大误差。 2-13对某电阻进行15次等精度重复测量,测得数据为28.53、28.52、28.50、28.52、 28.53、28.53、28.50、28.49、28.49、28.51、28.53、28.52、28.49、28.40、28.50, 单位为,试求: (1)平均值和标准差: (2)用拉依达准则判别该测量列中是否含有粗大误差的测量值,若有则重 新计算平均值和标准差: (3)平均值的标准差: (4)在置信概率为0.99时,写出测量结果的表达式。 解:(1) x1=28.504 i=1 6 ∑1(x1-习 =0.033 n-1 (2)用拉依达准则有,测量值28.40属于粗大误差,剔除,重新计算得 '=28.511 =0.018 (3)剔除粗大误差后,剩余测量值中不再含粗大误差,平均值'=28.511, 其标准差0=嘉=0.048 (4)当置信概率为0.99时,k=2.58,则△m=±(Ko)=±0.012V 由于测量有效位数影响,测量结果表示为Ux=可x±△m=28.51士0.01V 2-14通过电阻R的电流/产生热量(单位为J)Q=PR,式中的t为通过电流的 持续时间,已知/与R测量相对误差为1%,t测量的相对误差为5%,试求 Q的相对误差。 解: Q=I2Rt,δo=2IRtδ1+I2tδR+I2Rδ, 29+2+4=2×1%+1%+5%=8% δ0 R t
解:按照狄克松准则,n=10 时,按 r11 判别,若给定的置信概率为 0.95,查 表 2-4 得 𝑟11 = 𝑥(𝑛) − 𝑥(𝑛−1) 𝑥(𝑛) − 𝑥(2) = 25.53 − 25.51 25.53 − 25.47 = 2 6 ≈ 0.333 𝑟11 ′ = 𝑥(2) − 𝑥(1) 𝑥(𝑛−1) − 𝑥(1) = 25.47 − 25.46 25.51 − 25.46 = 0.2 因为𝑟11、𝑟11 ′ 都小于 0.477,故判定此 10 次测量值不含粗大误差。 2-13 对某电阻进行 15 次等精度重复测量,测得数据为 28.53、28.52、28.50、28.52、 28.53、28.53、28.50、28.49、28.49、28.51、28.53、28.52、28.49、28.40、28.50, 单位为 Ω,试求: (1) 平均值和标准差; (2) 用拉依达准则判别该测量列中是否含有粗大误差的测量值,若有则重 新计算平均值和标准差; (3) 平均值的标准差; (4) 在置信概率为 0.99 时,写出测量结果的表达式。 解:(1) 𝑥̅= 1 𝑛 ∑𝑥𝑖 = 28.504 𝑛 𝑖=1 𝜎̂ = √ ∑ (𝑥𝑖 − 𝑥̅) 𝑛 𝑖=1 𝑛 − 1 =0.033 (2)用拉依达准则有,测量值 28.40 属于粗大误差,剔除,重新计算得 𝑥̅ ′ = 28.511 σ̂ ′ = 0.018 (3)剔除粗大误差后,剩余测量值中不再含粗大误差,平均值𝑥̅ ′ = 28.511, 其标准差𝜎 ‘ = σ̂ ′ √14 = 0.0048 (4)当置信概率为 0.99 时,k=2.58,则∆𝑚= ±(𝐾𝜎 ′ ) = ±0.012𝑉 由于测量有效位数影响,测量结果表示为𝑈𝑥 = 𝑈̅𝑥 ± ∆𝑚= 28.51 ± 0.01𝑉 2-14通过电阻 R 的电流 I 产生热量(单位为 J) 2 Q I Rt ,式中的 t 为通过电流的 持续时间,已知 I 与 R 测量相对误差为 1%,t 测量的相对误差为 5%,试求 Q 的相对误差。 解: Q = I 2𝑅𝑡, 𝛿𝑄 = 2𝐼𝑅𝑡𝛿1 + I 2 𝑡𝛿𝑅 + I 2𝑅𝛿𝑡 , 𝛿𝑄 𝑄 = 2 𝛿𝐼 𝐼 + 𝛿𝑅 𝑅 + 𝛿𝑡 𝑡 = 2 × 1% + 1% + 5% = 8%