
ME369 Modeling,Analysis and System Control Fall 2014 Yuan Jianjun(袁建军) Associate Professor,Robotics Institute Office:Room 401,Building B of ME School yuanjj@sjtu.edu.edu.cn 021-34205559
Yuan Jianjun (袁建军) Associate Professor, Robotics Institute Office: Room 401, Building B of ME School yuanjj@sjtu.edu.edu.cn 021-34205559 ME369 Modeling, Analysis and System Control Fall 2014
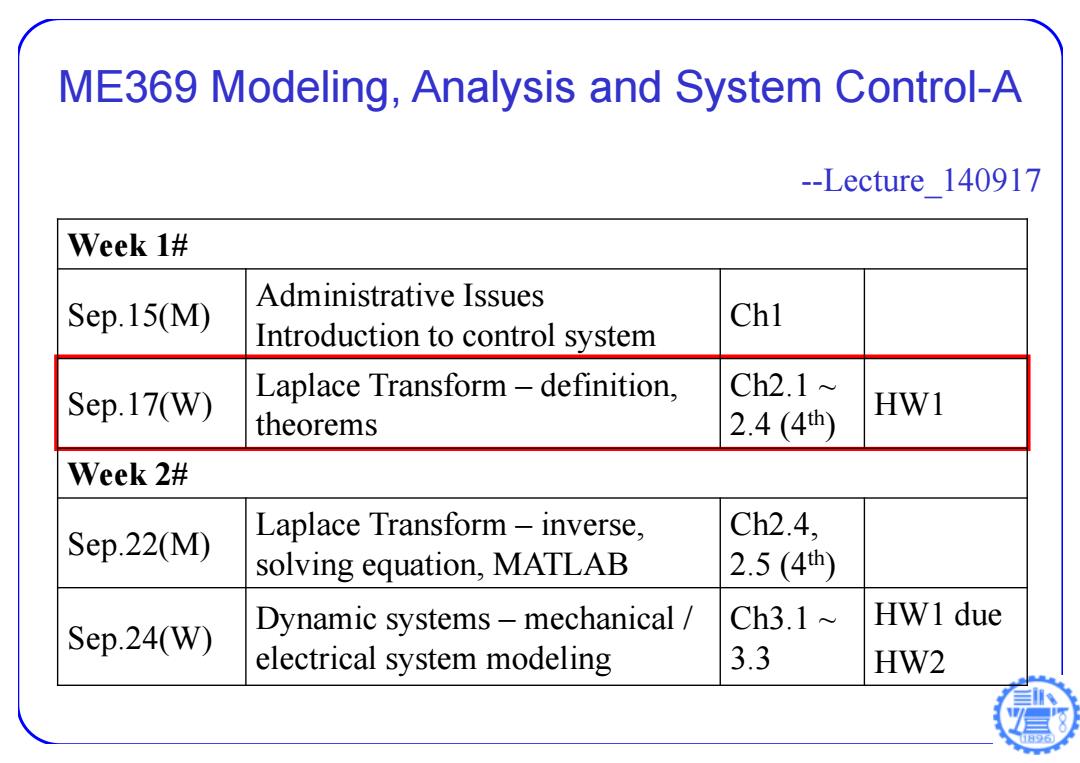
ME369 Modeling,Analysis and System Control-A --Lecture 140917 Week 1# Administrative Issues Sep.15(M) Ch1 Introduction to control system Sep.17(W) Laplace Transform-definition, Ch2.1~ 2.4(4) HW1 theorems Week 2# Sep.22(M) Laplace Transform-inverse, Ch2.4, solving equation,MATLAB 2.5(4h) Dynamic systems-mechanical Ch3.1 HW1 due Sep.24(W) electrical system modeling 3.3 HW2
ME369 Modeling, Analysis and System Control-A --Lecture_140917 Week 1# Sep.15(M) Administrative Issues Introduction to control system Ch1 Sep.17(W) Laplace Transform – definition, theorems Ch2.1 ~ 2.4 (4th ) HW1 Week 2# Sep.22(M) Laplace Transform – inverse, solving equation, MATLAB Ch2.4, 2.5 (4th ) Sep.24(W) Dynamic systems – mechanical / electrical system modeling Ch3.1 ~ 3.3 HW1 due HW2

Problems of HW1 ·Refer to the ftp site. .ftp://public.sjtu.edu.cn ·User:yuanjj ·Password:public DUE:Sep.24 (W)
Problems of HW1 • Refer to the ftp site. • ftp://public.sjtu.edu.cn • User: yuanjj • Password: public DUE: Sep.24 (W)

Definition of Laplace Transform Definition of Laplace Transform The Laplace Transform of f(t)is defined as F(s)=f(t)e-dt=[f() S=0+j0 Function ft)that satisfies 1.A time continuous function; 2.Real function; 3.t)=0,for0: 4 0f(t)eh<w→limf()e=0
• Definition of Laplace Transform • The Laplace Transform of f(t) is defined as 0 ( ) ( ) [ ( )] st F s f t e dt f t L lim ( ) 0 st t f te 0 ( ) st f t e dt Definition of Laplace Transform s j Function f(t) that satisfies 1. A time continuous function; 2. Real function; 3. f(t)=0, for t<0; 4

Laplace Transform of Typical Function 1.Exponential Function- 4.Sinusoidal Function [f(t)=0 for t<0 f(t)=0 for t<0 f(t)=Ae-for t≥0 f(t)=Asin ot for t≥0 2.Step Function f(t)=0 for t<0 ww-Sudv+Svdu f(t)=A for t≥0 3.Ramp Function Euler's Theorem f(t)=0 for t<0 f(t)=At for t≥0 coso1-em+em)
Laplace Transform of Typical Function 2. Step Function ( ) for 0 ( ) 0 for 0 f t A t f t t 3. Ramp Function ( ) for 0 ( ) 0 for 0 f t At t f t t uv udv vdu ( ) sin for 0 ( ) 0 for 0 f t A t t f t t 1.Exponential Function- 4. Sinusoidal Function ( ) for 0 ( ) 0 for 0 f t Ae t f t t t Euler’s Theorem

Existence of Laplace Transform Requirents of Time-Domain Function Given a function f(t)that satisfies (1)f(t)is a time function such that f(t)=0 for t0,and f(t)is exponential order as t approaches infinity. Exponential order A function f(t)is said to be of exponential order if a real,positive constant exists such that the function e|ft→0ast→o spacatv.)0aa. Abscissa of convergence
• Requirents of Time-Domain Function – Given a function f(t) that satisfies (1) f(t) is a time function such that f(t)=0 for t0, and f(t) is exponential order as t approaches infinity. – Exponential order A function f(t) is said to be of exponential order if a real,positive constant exists such that the function Existence of Laplace Transform e f t t t ( ) 0 as c 0 c lim e f ( t ) t t c Abscissa of convergence Specially, if

Example 1.f)=t2 d(t2) lim e-t2 =lim dt 2t 2 三 lim lim =0 t-.0 t-.0 d(e) t-.00 G" dt 2.f(t)=te-c lim e-ote-=0 o+C>0 Only if exists t-.o0 σ>-C
Example 0 2 lim 2 lim ( ) ( ) lim lim 2 . 2 . 2 . t t t t t t t e e t dt d e dt d t e t 2 1. f(t) t ct te 2. f(t) lim 0 . t ct t e te Only if c exists c 0

Example 3.ft)=e2 lim e-ae=lim e-)=co t-0 t-.0
Example ( ) . . 2 2 lim lim t t t t t e e e 2t 3. f(t) e

Definition of Laplace Transform Definition of Laplace Transform Given a function f(t)that satisfies 0fu)erdt<o→ lim f(t)e=0 t0 for some positive real o.The Laplace Transform of f(t)is defined as F(s)=∫nf(r)edt=[f(t】 Do we have to worry about the "existence condition"of F(s)? As long as the time function f(t)does not grow faster than exponentially, its Laplace Transform always exists.This condition is satisfied by all response signals of physical systems
• Definition of Laplace Transform – Given a function f(t) that satisfies 0 ( ) ( ) [ ( )] st F s f t e dt f t L Do we have to worry about the “existence condition” of F(s)? As long as the time function f(t) does not grow faster than exponentially, its Laplace Transform always exists. This condition is satisfied by all response signals of physical systems. lim ( ) 0 t t f te 0 ( ) t f t e dt for some positive real . The Laplace Transform of f(t) is defined as Definition of Laplace Transform

Laplace Transform of Typical Function 1.Exponential Function- 4.Sinusoidal Function [f(t)=0 for tto A f(t)=At for t≥0 F(s)= f0=2or0<1<, to
Laplace Transform of Typical Function 1.Exponential Function- ( ) for 0 ( ) 0 for 0 f t Ae t f t t t 2. Step Function ( ) for 0 ( ) 0 for 0 f t A t f t t 3. Ramp Function ( ) for 0 ( ) 0 for 0 f t At t f t t ( ) sin for 0 ( ) 0 for 0 f t A t t f t t 4. Sinusoidal Function 5.Translated Function f t t t f t t t ( ) 1 ( ) for ( ) 1 ( ) 0 for 6.Pulse Function 0 0 0 ( ) for 0 ( ) 0 for 0 and t t t t t A f t f t t ( ) A F s s 2 ( ) A F s s