ME369 Modeling,Analysis and System Control-A --Lecture 140924 Week 2# Laplace Transform-inverse, Ch2.4, Sep.22(M) solving equation,MATLAB 2.5(4th) Dynamic systems-mechanical Ch3.1~ HW1 due Sep.24(W) electrical system modeling 3.3 HW2 Week 3#Rest Week 4# 0ct.6M)) Rest Dynamic systems- Ch3.1~ Oct.8(W) mechanical/electrical system 3.3 modeling
ME369 Modeling, Analysis and System Control-A --Lecture_140924 Week 2# Sep.22(M) Laplace Transform – inverse, solving equation, MATLAB Ch2.4, 2.5 (4th ) Sep.24(W) Dynamic systems – mechanical / electrical system modeling Ch3.1 ~ 3.3 HW1 due HW2 Week 3# Rest Week 4# Oct.6(M) Rest Oct.8(W) Dynamic systems – mechanical/electrical system modeling Ch3.1 ~ 3.3

Problems of HW2 ·Refer to the ftp site. ftp://public.sjtu.edu.cn ·User:yuanjj ·Password:public DUE:Oct.13(M)
Problems of HW2 • Refer to the ftp site. • ftp://public.sjtu.edu.cn • User: yuanjj • Password: public DUE: Oct. 13 (M)

Solving Linear,Time-Invariant Differential Equations By taking the Laplace Transform of each term in the given differential equation. The time solutions of the differential equations is obtained by finding the inverse transform of the dependent variable. -Considering the initial conditions. Example 9 Find the Solutions of differential equation a,b are constants. 求+3元+2x=0,x(0)=a,(0)=b
– By taking the Laplace Transform of each term in the given differential equation. – The time solutions of the differential equations is obtained by finding the inverse transform of the dependent variable. – Considering the initial conditions. Example 9 Find the Solutions of differential equation x 3x 2x 0, x0 a, x0 b a,b are constants. Solving Linear,Time-Invariant Differential Equations

Example 10 Find the Solutions of differential equation: 求+2x+5x=3,x(0)=0,x(0)=0
Example 10 Find the Solutions of differential equation: x 2x 5x 3, x0 0, x 0 0

The solutions of differential equations Ke-a K sin @t Kea sin wt Kte-at
The solutions of differential equations at Ke K sin t sin at Ke t at Kte
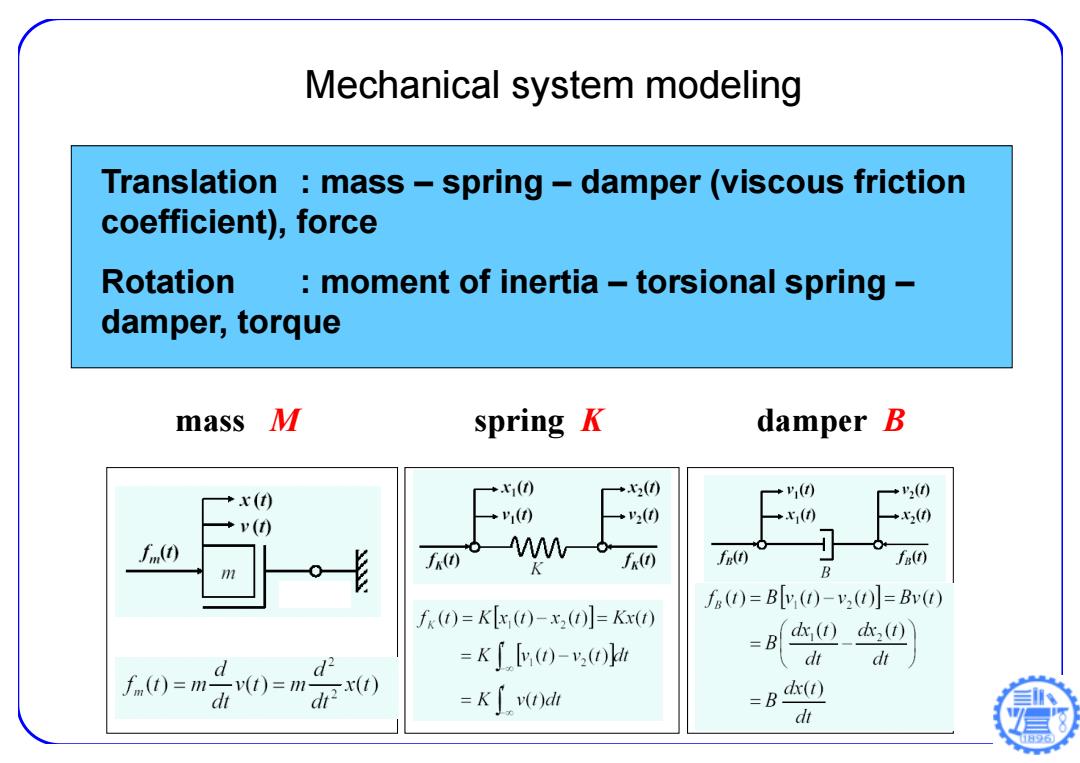
Mechanical system modeling Translation mass-spring -damper(viscous friction coefficient),force Rotation moment of inertia-torsional spring damper,torque mass M spring K damper B +x(0 →xz(0 →x(t) →(0 →2(0 一→10 →(0 +x1() +v(0 →(0 f.(() f() 8M 6- f() fe(t) fa(t) 71 K B fo(1)=Blv (1)-v2(1)=Bv(t) f()=K()-x2()]=Kx() =K(-v.( =B () (t) d d2 dt dt .0=m市0=m =KJv(dr =B( dt
Mechanical system modeling Translation : mass – spring – damper (viscous friction coefficient), force Rotation : moment of inertia – torsional spring – damper, torque mass M spring K damper B
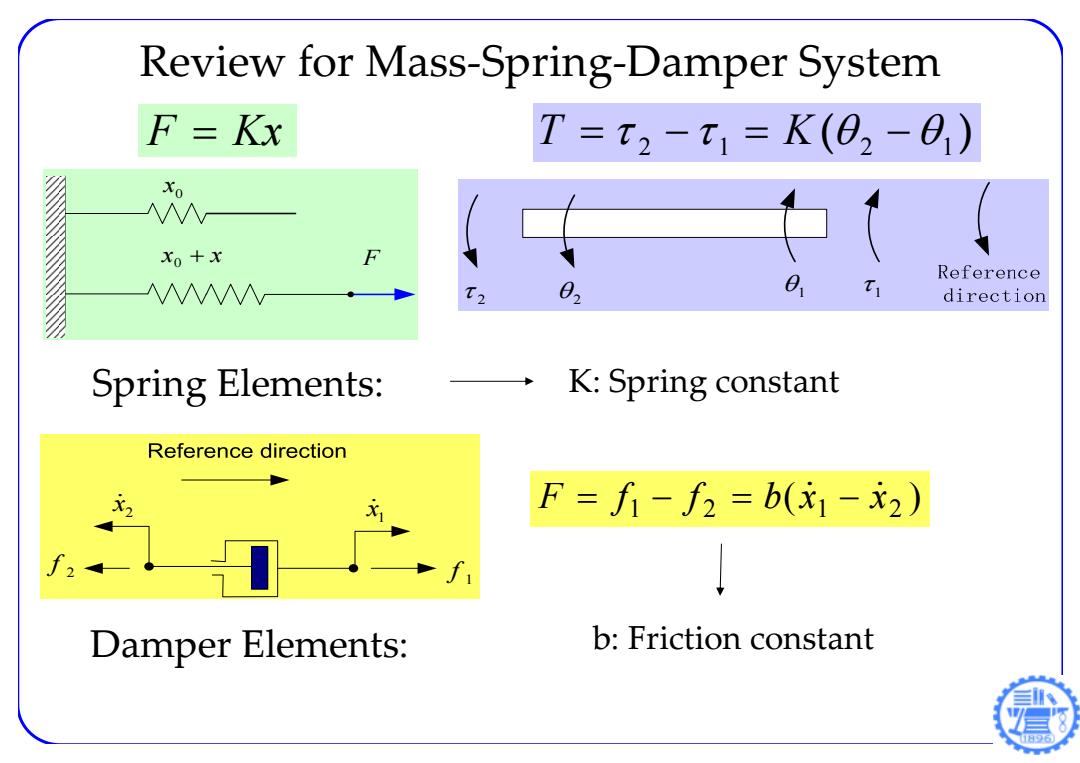
Review for Mass-Spring-Damper System F=Kx T=t2-t1=K(02-0) Xo Xo+x F 02 0、 Reference direction Spring Elements: K:Spring constant Reference direction F=f-f2=b(x1-x2) f Damper Elements: b:Friction constant
Review for Mass‐Spring‐Damper System 0 x x x 0 F Spring Elements: K: Spring constant ( ) 2 1 2 1 F Kx T K 2 1 2 1 1 x2 x 1 2 f f ( ) 1 2 1 2 F f f b x x Damper Elements: b: Friction constant

Review for Mass-Spring-Damper System Newton's second law ma=∑F Ja=∑T F=the vector sum of all forces applied to each body in a system,newtons (N)or pounds (lb) a the vector acceleration of each body with respect to an inertial reference frame.m/sec2 or ft/sec2 m=mass of the body.Kg or slug
Newton’s second law ma F J T F = the vector sum of all forces applied to each body in a system, newtons (N) or pounds (lb) a = the vector acceleration of each body with respect to an inertial reference frame. m/sec2 or ft/sec2 m = mass of the body. Kg or slug Review for Mass-Spring-Damper System
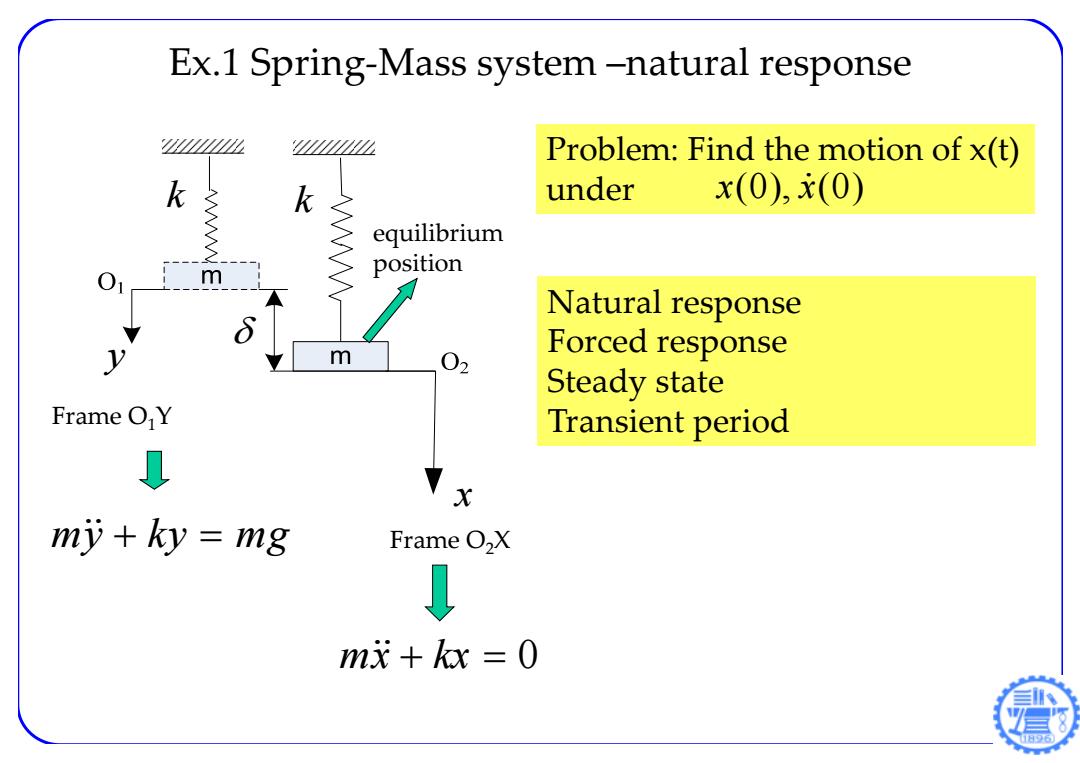
Ex.1 Spring-Mass system-natural response Problem:Find the motion of x(t) k k under x(0),x(0) equilibrium m position Natural response m 02 Forced response Steady state Frame OY Transient period L x my +ky =mg Frame O2X ↓ mx+kx=0
Ex.1 Spring‐Mass system –natural response equilibrium position Frame O1Y k k x y my ky mg Frame O2X m x kx 0 Problem: Find the motion of x(t) under x(0), x(0) Natural response Forced response Steady state Transient period
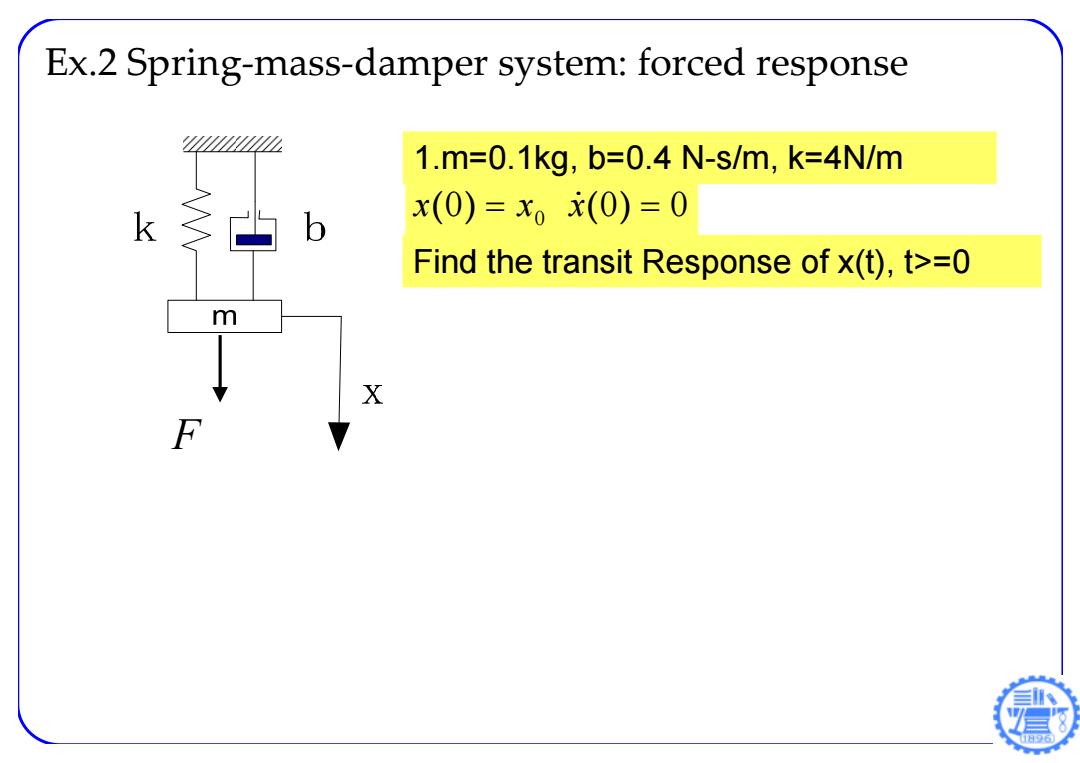
Ex.2 Spring-mass-damper system:forced response 1.m=0.1kg,b=0.4N-s/m,k=4N/m k b x(0)=x(0)=0 Find the transit Response of x(t),t>=0 m X
1.m=0.1kg, b=0.4 N-s/m, k=4N/m Ex.2 Spring ‐mass ‐damper system: forced response 0 0 0 x ( ) x 0 x( ) Find the transit Response of x(t), t>=0 F