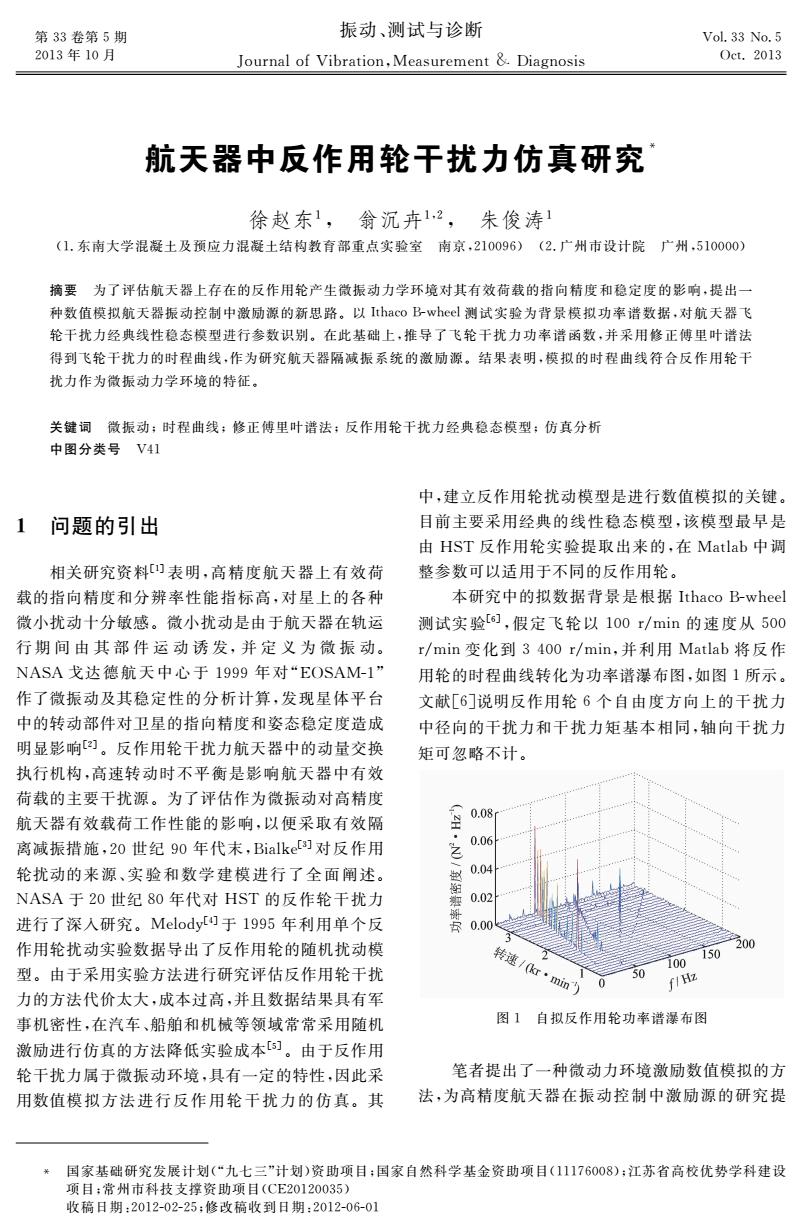
第33卷第5期 振动、测试与诊断 Vol.33 No.5 2013年10月 Journal of Vibration,Measurement &Diagnosis Oct.2013 航天器中反作用轮干扰力仿真研究 徐赵东1,翁沉卉12,朱俊涛1 (1.东南大学混凝土及预应力混凝土结构教育部重点实验室南京,210096)(2.广州市设计院广州,510000) 摘要为了评估航天器上存在的反作用轮产生微振动力学环境对其有效荷载的指向精度和稳定度的影响,提出一 种数值模拟航天器振动控制中激励源的新思路。以Ithaco B-wheel测试实验为背景模拟功率谱数据,对航天器飞 轮干扰力经典线性稳态模型进行参数识别。在此基础上,推导了飞轮干扰力功率谱函数,并采用修正傅里叶谱法 得到飞轮干扰力的时程曲线,作为研究航天器隔减振系统的激励源。结果表明,模拟的时程曲线符合反作用轮干 扰力作为微振动力学环境的特征。 关键词微振动:时程曲线;修正傅里叶谱法:反作用轮干扰力经典稳态模型:仿真分析 中图分类号V41 中,建立反作用轮扰动模型是进行数值模拟的关键。 1 问题的引出 目前主要采用经典的线性稳态模型,该模型最早是 由HST反作用轮实验提取出来的,在Matlab中调 相关研究资料)表明,高精度航天器上有效荷 整参数可以适用于不同的反作用轮。 载的指向精度和分辨率性能指标高,对星上的各种 本研究中的拟数据背景是根据Ithaco B-wheel 微小扰动十分敏感。微小扰动是由于航天器在轨运 测试实验[6],假定飞轮以100r/min的速度从500 行期间由其部件运动诱发,并定义为微振动。 r/min变化到3400r/min,并利用Matlab将反作 NASA戈达德航天中心于1999年对“EOSAM-1” 用轮的时程曲线转化为功率谱瀑布图,如图1所示。 作了微振动及其稳定性的分析计算,发现星体平台 文献[6]说明反作用轮6个自由度方向上的干扰力 中的转动部件对卫星的指向精度和姿态稳定度造成 中径向的干扰力和干扰力矩基本相同,轴向干扰力 明显影响)。反作用轮干扰力航天器中的动量交换 矩可忽略不计。 执行机构,高速转动时不平衡是影响航天器中有效 荷载的主要干扰源。为了评估作为微振动对高精度 航天器有效载荷工作性能的影响,以便采取有效隔 0.08 离减振措施,20世纪90年代末,Bialke]对反作用 之 0.06 轮扰动的来源、实验和数学建模进行了全面阐述。 0.04 NASA于20世纪80年代对HST的反作轮干扰力 0.02 进行了深入研究。Melody!)于1995年利用单个反 0.00 作用轮扰动实验数据导出了反作用轮的随机扰动模 200 转速/(kr·min) 150 100 型。由于采用实验方法进行研究评估反作用轮干扰 50 0 f/Hz 力的方法代价太大,成本过高,并且数据结果具有军 事机密性,在汽车、船舶和机械等领域常常采用随机 图1自拟反作用轮功率谱瀑布图 激励进行仿真的方法降低实验成本[)。由于反作用 轮干扰力属于微振动环境,具有一定的特性,因此采 笔者提出了一种微动力环境激励数值模拟的方 用数值模拟方法进行反作用轮干扰力的仿真。其 法,为高精度航天器在振动控制中激励源的研究提 国家基础研究发展计划(“九七三”计划)资助项目:国家自然科学基金资助项目(11176008):江苏省高校优势学科建设 项目:常州市科技支撑资助项目(CE20120035) 收稿日期:2012-02-25:修改稿收到日期:2012-06-01
书 第33卷第5期 2013年10月 振动、测试与诊断 JournalofVibration,Measurement& Diagnosis Vol.33No.5 Oct.2013 航天器中反作用轮干扰力仿真研究 徐赵东1, 翁沉卉1,2, 朱俊涛1 (1.东南大学混凝土及预应力混凝土结构教育部重点实验室 南京,210096) (2.广州市设计院 广州,510000) 摘要 为了评估航天器上存在的反作用轮产生微振动力学环境对其有效荷载的指向精度和稳定度的影响,提出一 种数值模拟航天器振动控制中激励源的新思路。以IthacoBwheel测试实验为背景模拟功率谱数据,对航天器飞 轮干扰力经典线性稳态模型进行参数识别。在此基础上,推导了飞轮干扰力功率谱函数,并采用修正傅里叶谱法 得到飞轮干扰力的时程曲线,作为研究航天器隔减振系统的激励源。结果表明,模拟的时程曲线符合反作用轮干 扰力作为微振动力学环境的特征。 关键词 微振动;时程曲线;修正傅里叶谱法;反作用轮干扰力经典稳态模型;仿真分析 中图分类号 V41 1 问题的引出 相关研究资料[1]表明,高精度航天器上有效荷 载的指向精度和分辨率性能指标高,对星上的各种 微小扰动十分敏感。微小扰动是由于航天器在轨运 行 期 间 由 其 部 件 运 动 诱 发,并 定 义 为 微 振 动。 NASA 戈达德航天中心于 1999 年对“EOSAM1” 作了微振动及其稳定性的分析计算,发现星体平台 中的转动部件对卫星的指向精度和姿态稳定度造成 明显影响[2]。反作用轮干扰力航天器中的动量交换 执行机构,高速转动时不平衡是影响航天器中有效 荷载的主要干扰源。为了评估作为微振动对高精度 航天器有效载荷工作性能的影响,以便采取有效隔 离减振措施,20世纪90年代末,Bialke[3]对反作用 轮扰动的来源、实验和数学建模进行了全面阐述。 NASA 于20世纪80年代对 HST 的反作轮干扰力 进行了深入研究。Melody[4]于1995年利用单个反 作用轮扰动实验数据导出了反作用轮的随机扰动模 型。由于采用实验方法进行研究评估反作用轮干扰 力的方法代价太大,成本过高,并且数据结果具有军 事机密性,在汽车、船舶和机械等领域常常采用随机 激励进行仿真的方法降低实验成本[5]。由于反作用 轮干扰力属于微振动环境,具有一定的特性,因此采 用数值模拟方法进行反作用轮干扰力的仿真。其 中,建立反作用轮扰动模型是进行数值模拟的关键。 目前主要采用经典的线性稳态模型,该模型最早是 由 HST 反作用轮实验提取出来的,在 Matlab中调 整参数可以适用于不同的反作用轮。 本研究中的拟数据背景是根据IthacoBwheel 测试实验[6],假定飞轮以 100r/min的速度从 500 r/min变化到3400r/min,并利用 Matlab将反作 用轮的时程曲线转化为功率谱瀑布图,如图1所示。 文献[6]说明反作用轮6个自由度方向上的干扰力 中径向的干扰力和干扰力矩基本相同,轴向干扰力 矩可忽略不计。 图1 自拟反作用轮功率谱瀑布图 笔者提出了一种微动力环境激励数值模拟的方 法,为高精度航天器在振动控制中激励源的研究提 国家基础研究发展计划(“九七三”计划)资助项目;国家自然科学基金资助项目(11176008);江苏省高校优势学科建设 项目;常州市科技支撑资助项目(CE20120035) 收稿日期:20120225;修改稿收到日期:20120601

882 振动、测试与诊断 第33卷 供了一种新的思路。首先,利用拟数据对反作用轮 舍弃。落在较大振幅范围内的峰值标号为0,则视 的经典线性稳态模型进行参数识别:然后,推导其功 为谐波干扰。采用瀑布图可看出某一谐波级次对应 率谱密度函数:最后,用修正的傅里叶谱法模拟反作 的干扰力功率谱基本是成线性变化,可建立不同飞 用轮一个自由度方向的干扰力,得到其时程曲线和 轮速度的完整峰值-谐波级次矩阵,即确立谐波级 功率谱密度图。仿真结果表明,反作用轮干扰力在 次,见表1。 时域上具有微振动振幅小、频率高的特征,符合高精 0.25f 度航天器运行的动力学环境,因此能应用于航天器 0.20 中隔减振平台的评估研究。该方法具有简便易行、 0.15 适用性广的特点。 婴0.10 2反作用轮线性稳态模型 0.05 反作用轮的干扰力线性稳态模型是一系列谐波 0.00020406080100120140160180200 f/Hz 函数的叠加,可表达为与反作用轮速度平方成比例 (a)频谱曲线 的离散谐函数[) 0.25F F(t)=>Cifisin(2xhif+) 0.20 (1) 0.15 其中:F(t)为干扰力:f为反作用轮转速;n为模型 马 0.10 中谐波的数目;C:为第i阶谐波的振幅系数;h,为 谐波级次;g:为[0,2π]区间内的随机相位。 0.05 whwn-mwwhwwr 反作用轮干扰力的经典线性稳态模型采用如下 0.000.00.51.01.52.02.5 5 假定: 归一化频率 1)假定干扰力是一系列关于反作用轮速度的 b)归一化频谱曲线 离散谐波函数; 图2 B-wheel在3400r/min时的频谱曲线 2)每段观测时间内忽略反作用轮速度的变化 3.2振幅系数的计算 的瞬态效应,假定反作用轮速度在微小时间段内为 一个常数值; 第2步就是要确定振幅系数。假定干扰力与反 3)不考虑反作用轮内部的柔顺机构在某一特 作用轮速度的平方成正比例关系,可表达为 定速度时模态对干扰力谐函数增幅的影响。 F=CQ: (2) 其中:F:为第i阶谐波的干扰力;C:为第i阶谐波的 3 经典稳态模型的参数识别 振幅系数;2,为第i阶谐波的飞轮速度。 振幅系数可采用最小二乘法计算得到,如式(3) 3.1谐波级次的确定 所示。第i阶谐波的第j级反作用轮速度对应干扰 力F,的理论值和实验值的误差e,的平方为 建立经验模型的第1步就是要根据图(1)所示 e号=(C2-F,)2 (3) 的拟数据功率谱瀑布图确定飞轮干扰的非整数谐波 对所有反作用轮速度对应干扰力的误差平方求 级次:。首先,将由反作用轮旋转速度对应的频率 最小值后得到第i阶谐波振幅系数C: 向量进行归一化,如图2所示,图2(a)是对应于 C,=∑,Fn/∑,n (4) 3400r/min的频谱曲线,图2(b)则将图2(a)x轴频 图3所示的是谐波级次h:分别为1.00和3.84 率进行归一化;然后,对飞轮每个旋转速度对应的归 对应的B-wheel干扰力-振幅系数曲线。由图3(a) 一化频谱曲线搜索峰值,因为并不是幅频曲线上所 可以看出,对于基谐波假设的方程(2)与实验数据得 有的峰值点都是谐波干扰,有些是由于进行快速傅 到了较好的吻合。图3(b)表明了方程(2)假设的 里叶变换而产生的噪声和波瓣。为了把噪声和谐波 力-速度关系并不适用于高次谐波;因此,如果求得 干扰区分开,将干扰力的振幅峰值进行分类标号,设 的力-速度曲线与实验数据的拟合度不高的话,应该 落在较小振幅范围内的峰值标号为1,并视为噪声 舍弃该谐波级次
供了一种新的思路。首先,利用拟数据对反作用轮 的经典线性稳态模型进行参数识别;然后,推导其功 率谱密度函数;最后,用修正的傅里叶谱法模拟反作 用轮一个自由度方向的干扰力,得到其时程曲线和 功率谱密度图。仿真结果表明,反作用轮干扰力在 时域上具有微振动振幅小、频率高的特征,符合高精 度航天器运行的动力学环境,因此能应用于航天器 中隔减振平台的评估研究。该方法具有简便易行、 适用性广的特点。 2 反作用轮线性稳态模型 反作用轮的干扰力线性稳态模型是一系列谐波 函数的叠加,可表达为与反作用轮速度平方成比例 的离散谐函数[6] 犉(狋)=∑ 狀 犻=1 犆犻犳2 狉ω犪sin(2π犺犻犳狉ω犪狋+φ犻) (1) 其中:犉(狋)为干扰力;犳狉ω犪为反作用轮转速;狀为模型 中谐波的数目;犆犻 为第犻 阶谐波的振幅系数;犺犻 为 谐波级次;φ犻 为[0,2π]区间内的随机相位。 反作用轮干扰力的经典线性稳态模型采用如下 假定: 1)假定干扰力是一系列关于反作用轮速度的 离散谐波函数; 2)每段观测时间内忽略反作用轮速度的变化 的瞬态效应,假定反作用轮速度在微小时间段内为 一个常数值; 3)不考虑反作用轮内部的柔顺机构在某一特 定速度时模态对干扰力谐函数增幅的影响。 3 经典稳态模型的参数识别 3.1 谐波级次的确定 建立经验模型的第1步就是要根据图(1)所示 的拟数据功率谱瀑布图确定飞轮干扰的非整数谐波 级次犺犻。首先,将由反作用轮旋转速度对应的频率 向量进行 归 一 化,如 图 2 所 示,图 2(a)是 对 应 于 3400r/min的频谱曲线,图2(b)则将图2(a)狓轴频 率进行归一化;然后,对飞轮每个旋转速度对应的归 一化频谱曲线搜索峰值,因为并不是幅频曲线上所 有的峰值点都是谐波干扰,有些是由于进行快速傅 里叶变换而产生的噪声和波瓣。为了把噪声和谐波 干扰区分开,将干扰力的振幅峰值进行分类标号,设 落在较小振幅范围内的峰值标号为1,并视为噪声 舍弃。落在较大振幅范围内的峰值标号为0,则视 为谐波干扰。采用瀑布图可看出某一谐波级次对应 的干扰力功率谱基本是成线性变化,可建立不同飞 轮速度的完整峰值谐波级次矩阵,即确立谐波级 次,见表1。 图2 Bwheel在3400r/min时的频谱曲线 3.2 振幅系数的计算 第2步就是要确定振幅系数。假定干扰力与反 作用轮速度的平方成正比例关系,可表达为 犉犻 =犆犻Ω2 犻 (2) 其中:犉犻 为第犻阶谐波的干扰力;犆犻 为第犻阶谐波的 振幅系数;Ω犻 为第犻阶谐波的飞轮速度。 振幅系数可采用最小二乘法计算得到,如式(3) 所示。第犻阶谐波的第犼级反作用轮速度对应干扰 力犉犻犼的理论值和实验值的误差犲犻犼的平方为 犲2 犻犼 =(犆犻Ω2 犼 -犉犻犼)2 (3) 对所有反作用轮速度对应干扰力的误差平方求 最小值后得到第犻阶谐波振幅系数犆犻 犆犻 =∑犼 犉犻犼Ω2 犼/∑犼 Ω4 犼 (4) 图3所示的是谐波级次犺犻 分别为1.00和3.84 对应的 Bwheel干扰力振幅系数曲线。由图3(a) 可以看出,对于基谐波假设的方程(2)与实验数据得 到了较好的吻合。图 3(b)表明了方程(2)假设的 力速度关系并不适用于高次谐波;因此,如果求得 的力速度曲线与实验数据的拟合度不高的话,应该 舍弃该谐波级次。 882 振 动、测 试 与 诊 断 第33卷

第5期 徐赵东,等:航天器中反作用轮干扰力仿真研究 883 果加以整理,同时根据图中各个谐波级次对应的曲 0.25 线的拟合度可以对振幅系数进行修正和取舍,结果 0.20 如表1所示,只取前3阶谐波级次所对应的谐波 0.15 级次。 表1振幅系数修正表 0.10 谐波级次h: 振幅系数C 修正系数C: 0.05 1.00 21.90 20.90 1.99 15.20 7.71 0.00 0.5 1.0 1.5 2.0 2.5 3.0 3.5 3.18 13.40 13.40 转速/kr·min 3.84 11.20 (ah=1.00 舍弃 4.56 9.19 舍弃 0.08 0.07 5.04 7.79 舍弃 6.00 6.77 舍弃 0.06 6.60 5.96 舍弃 0.05 8.53 5.30 舍弃 0.04 9.36 4.78 舍弃 0.03 12.48 4.53 舍弃 0.02 0.01 4 0.00 反作用轮干扰力功率谱密度函数的 0.5 1.0 1.5 2.0 2.5 3.03.5 转速/Ckr·min 推导 (b)h=3.84 图3B-wheel径向轴力的振幅系数曲线 根据式(1),并由于在[02π]范围内的随机变 量:和9,是相互独立的,得反作用轮干扰力的自 图4所示的是谐波级次:为1.99对应的 相关函数[-]如下 B-wheel径向轴力振幅系数曲线。图4可看出,在 R(t)=E[m(t)m(t-r)]= 1300~1900r/min千扰力的振幅激增。这是因为 当谐波频率和飞轮自身模态频率相同时,会发生共 ECsin()x 振。但在经验稳态线性模型中不考虑飞轮自身模态 sin(2mhif na (t+r)+i)]= 对干扰力谐波函数的影响,则在采用式(4)计算振幅 系数时应当去除这些点,表明飞轮的内部自身模态 2cEL1-a+22× 2 对干扰力也会产生一定的影响。 cos(2πh:fumx)- 0.18 。飞轮模态影响 sin(fsin(2)] (5) 0.16 O不考虑飞轮模态影响 0.14 根据期望定义得到式(6)的关系 0.12 "2n E[cos(2ot+2g)]= J。cos(2wt+2g) 0.10 云0 0 0.08 0 E[sin(2ot +2i)]= sm(2a+24)2云4=0 0.06 (6) 0.04 00 0.02 因此,自相关函数可表达为 0.000.5 1.0 1.5 2.0 2.5 3.0 3.5 R(r)= 转速/kr·min) 2cE[fo2hfr】 (7) 对式(5)进行傅里叶变换,假设飞轮转速是随机 图4h=l.99时B-wheel径向轴力的振幅系数曲线 变量,其概率密度函数为f,(u),欧拉公式如下 根据以上方法,在Matlab中绘制所有谐波级次 coS.I (ekteu) 1 (8) 所对应的干扰力-转速曲线。将计算的振幅系数结 根据式(8)得到自相关函数的变形为
图3 Bwheel径向轴力的振幅系数曲线 图4 所 示 的 是 谐 波 级 次 犺犻 为 1.99 对 应 的 Bwheel径向轴力振幅系数曲线。图 4 可看出,在 1300~1900r/min干扰力的振幅激增。这是因为 当谐波频率和飞轮自身模态频率相同时,会发生共 振。但在经验稳态线性模型中不考虑飞轮自身模态 对干扰力谐波函数的影响,则在采用式(4)计算振幅 系数时应当去除这些点,表明飞轮的内部自身模态 对干扰力也会产生一定的影响。 图4 犺=1.99时 Bwheel径向轴力的振幅系数曲线 根据以上方法,在 Matlab中绘制所有谐波级次 所对应的干扰力转速曲线。将计算的振幅系数结 果加以整理,同时根据图中各个谐波级次对应的曲 线的拟合度可以对振幅系数进行修正和取舍,结果 如表1 所示,只取前 3 阶 谐 波 级 次 所 对 应 的 谐 波 级次。 表1 振幅系数修正表 谐波级次犺犻 振幅系数犆犻 修正系数犆′犻 1.00 21.90 20.90 1.99 15.20 7.71 3.18 13.40 13.40 3.84 11.20 舍弃 4.56 9.19 舍弃 5.04 7.79 舍弃 6.00 6.77 舍弃 6.60 5.96 舍弃 8.53 5.30 舍弃 9.36 4.78 舍弃 12.48 4.53 舍弃 4 反作用轮干扰力功率谱密度函数的 推导 根据式(1),并由于在[0 2π]范围内的随机变 量φ犻 和φ犼 是相互独立的,得反作用轮干扰力的自 相关函数[78]如下 犚犿(τ)=犈[犿(狋)犿(狋-τ)]= 犈[∑ 狀 犻=1 犆2 犻犳4 狉狑犪sin(2π犺犻犳狉狑犪狋+φ犻)× sin(2π犺犻犳狉狑犪(狋+τ)+φ犻)]= ∑ 狀 犻=1 犆2 犻犈[犳4 狉狑犪{1-cos(4π犺犻犳狉狑犪狋+2φ犻) 2 × cos(2π犺犻犳狉狑犪τ)- sin(4π犺犻犳狉狑犪狋+2φ犻) 2 sin(2π犺犻犳狉狑犪τ)}] (5) 根据期望定义得到式(6)的关系 犈[cos(2ω狋+2φ犻)]=∫ 2π 0 cos(2ω狋+2φ犻)1 2π dφ= 0 犈[sin(2ω狋+2φ犻)]=∫ 2π 0 sin(2ω狋+2φ犻)1 2π dφ= 烅 烄 烆 0 (6) 因此,自相关函数可表达为 犚犿(τ)=∑ 狀 犻=1 犆2 犻犈[犳4 狉狑犪cos(2π犺犻犳狉狑犪τ)] (7) 对式(5)进行傅里叶变换,假设飞轮转速是随机 变量,其概率密度函数为犳狆(狌),欧拉公式如下 cos狓=1 2(犲犻狓 +犲-犻狓 ) (8) 根据式(8)得到自相关函数的变形为 第5期 徐赵东,等:航天器中反作用轮干扰力仿真研究 883

884 振动、测试与诊断 第33卷 R(x)- 2 f (u)du (9) 3)根据式(16)将傅里叶幅值谱F(w)结合随机 相位g转化成复数形式C(w) 令2xh,u=u,作变量代换u一2得 C(@)=F(@)ei (16) 4)对C()进行傅里叶变换,并取实部作为生 wer十er 成的时程y 2xhi (I(a)=ifft(C(@)) (10) (17) y=real(I(@)) 进一步变量代换ω=一,得到自相关函数的傅 5)重复步骤3和步骤4。 里叶变换表达式 根据以上步骤在Matlab中编程),得到反作 R.()= 号前,盒+ 用轮的时程曲线,如图5所示。 2πh: 0.015 含鄂gf,孟d (11) 由式(12)所示维纳-辛钦定理中自相关函数和 0.000 功率谱密度之间的傅里叶变换关系为 R(t)= 1 Φn(u)erdw (12) 2元」-∞ 0.0156.0 0.4 0.6 0.8 1.0 得到反作用轮的功率谱密度函数为 t/s (a)修正傅里叶谱法生成的反作用轮500rmin时干扰力时程曲线 Φn(u)= πCw 22f,2.)+f,】 (13) 由于以上假定反作用轮在每一小段时间内的转 速是常数,并且是在[f1f2]的均匀分布的随机 变量,则飞轮的功率谱密度函数为 0.0 0.4 0.6 0.8 1.0 Φn(u)=∑更,(u) t/s (b)修正傅里叶谱法生成的反作用轮1500rmin时干扰力时程曲线 πCw' 2(f2-f1)(2xh:)5 重(w)= (14) (2xh:f1<|w|<2πh:f2) 0 其他 修正傅里叶谱法模拟反作用轮的时 程曲线 0260 0.2 0.4 0.6 0.8 1.0 t/s (c)修正傅里叶谱法生成的反作用轮2500min时干扰力时程曲线 由式(14)可知,在[f1f2]内功率谱密度函数 图5修正傅里叶谱法生成的反作用轮干扰力时程 是一常数,类似白噪声町;因此,可采用修正的傅里 叶谱法利用推导得到的功率谱密度函数生成相应的 图5为反作用轮在转速分别为500,1500, 时程曲线,其基本步骤如下[1。 2500r/min时采用修正傅里叶谱法生成的反作用 1)由自功率谱密度函数S(ω)计算其所对应的 轮干扰力时程曲线。可以看出,干扰力的幅值都较 傅里叶幅值谱F(u) 小,符合微振动的特征。由于反作用轮不平衡性也具 F(u)=(4S(w)2πf)t (15) 有随机性,均匀转速产生的干扰力也具有随机特征, nfft 且随着反作用轮转速的增大,产生的干扰力的幅值也 其中:f,为生成随机振动时程的采样频率:nfft为傅 逐渐增大。本研究采用的方法依然能够将航天器中 里叶变换长度,一般取S(ω)中元素个数的2倍。 反作用轮干扰力作为微振动源的特性仿真出来,而且 2)按照均匀分布在0一2π之间生成随机相位 方法简便,计算效率高,且不需耗费巨大的实验费用, 信息g。 可以作为评估航天器减振平台工作性能的激励源
犚犿(τ)=∑ 狀 犻=1 犆2 犻 2∫ ∞ -∞ 狌4犲犻2π犺犻狌τ +犲-犻2π犺犻狌τ 2 犳狆(狌)d狌 (9) 令2π犺犻狌=ω,作变量代换狌= ω 2π犺犻 得 犚犿(τ)=∑ 狀 犻=1 犆2 犻 2∫ ∞ -∞ ω4 (2π犺犻)5 犲犻ωτ +犲-犻ωτ 2 犳狆(ω 2π犺犻 )dω (10) 进一步变量代换ω=-狏,得到自相关函数的傅 里叶变换表达式 犚犿(ω)=∑ 狀 犻=1 犆2 犻 2∫ ∞ -∞ ω4 (2π犺犻)5犲犻ωτ 犳狆(ω 2π犺犻 )dω+ ∑ 狀 犻=1 犆2 犻 2∫ ∞ -∞ ω4 (2π犺犻)5犲-犻狏τ 犳狆(-ω 2π犺犻 )dω (11) 由式(12)所示维纳辛钦定理中自相关函数和 功率谱密度之间的傅里叶变换关系为 犚犿(τ)= 1 2π∫ ∞ -∞ Φ犿(ω)犲犻ωτdω (12) 得到反作用轮的功率谱密度函数为 Φ犿(ω)=∑ 狀 犻=1 π犆2 犻ω4 2(2π犺犻)5[犳狆(ω 2π犺犻 )+犳狆(-ω 2π犺犻 )] (13) 由于以上假定反作用轮在每一小段时间内的转 速是常数,并且是在[犳1 犳2 ]的均匀分布的随机 变量,则飞轮的功率谱密度函数为 Φ犿(ω)=∑ 狀 犻=1 Φ犻(ω) Φ犻(ω)= π犆2 犻ω4 2(犳2 -犳1)(2π犺犻)5 (2π犺犻犳1 <狘ω狘<2π犺犻犳2) 0 烅 烄 烆 其他 (14 烅 烄 烆 ) 5 修正傅里叶谱法模拟反作用轮的时 程曲线 由式(14)可知,在[犳1 犳2]内功率谱密度函数 是一常数,类似白噪声[9];因此,可采用修正的傅里 叶谱法利用推导得到的功率谱密度函数生成相应的 时程曲线,其基本步骤如下[10]。 1)由自功率谱密度函数犛(ω)计算其所对应的 傅里叶幅值谱犉(ω) 犉(ω)=(4犛(ω)2π犳狊 nfft ) 1 2 (15) 其中:犳狊 为生成随机振动时程的采样频率;nfft为傅 里叶变换长度,一般取犛(ω)中元素个数的2倍。 2)按照均匀分布在0~2π之间生成随机相位 信息犵。 3)根据式(16)将傅里叶幅值谱犉(ω)结合随机 相位犵转化成复数形式犆(ω) 犆(ω)=犉(ω)犲犻犵 (16) 4)对犆(ω)进行傅里叶变换,并取实部作为生 成的时程狔 犐(ω)=ifft(犆(ω)) {狔=real(犐(ω)) (17) 5)重复步骤3和步骤4。 根据以上步骤在 Matlab中编程[11],得到反作 用轮的时程曲线,如图5所示。 图5 修正傅里叶谱法生成的反作用轮干扰力时程 图5 为 反 作 用 轮 在 转 速 分 别 为 500,1500, 2500r/min时采用修正傅里叶谱法生成的反作用 轮干扰力时程曲线。可以看出,干扰力的幅值都较 小,符合微振动的特征。由于反作用轮不平衡性也具 有随机性,均匀转速产生的干扰力也具有随机特征, 且随着反作用轮转速的增大,产生的干扰力的幅值也 逐渐增大。本研究采用的方法依然能够将航天器中 反作用轮干扰力作为微振动源的特性仿真出来,而且 方法简便,计算效率高,且不需耗费巨大的实验费用, 可以作为评估航天器减振平台工作性能的激励源。 884 振 动、测 试 与 诊 断 第33卷

第5期 徐赵东,等:航天器中反作用轮干扰力仿真研究 885 [5]皮阳军,王宣银,罗晓晔,等.六自由度舰船运动模拟 6结束语 器随机海浪谱模拟[J门.振动、测试与诊断,2010,4 (30):375-378. 为了保证高精度航天器的有效载荷在微振动力 Pi Yangjun.Wang Xuanyin,Luo Xiaoye,et al.Simu- lation to random ocean wave spectrum using six de- 学环境下良好的工作性能,反作用轮干扰力作为主 grees of freedom ship motion simulator [J].Journal of 要的激励源,对其特性的研究分析有助于高精度航 Vibration.Measure 8.Diagnosis,2010,4 (30):375- 天器隔减振系统的评估分析。笔者以Ithaco B- 378.(in Chinese) wheel测试实验为背景进行数据模拟,在反作用轮 [6]Rebecca A M.David W M.Robert L G.Development 干扰力经典线性稳态模型的基础上,对其参数进行 of empirical and analytical reaction wheel disturbance 识别,推导了反作用轮干扰力的功率谱密度函数,并 models [C]//40th AIAA/ASCE/AHS/ASC Struc- 用修正的傅里叶谱法模拟了反作用轮干扰力的时程 tures,Structural Dynamics and Materials Conference. AIAA/ASME/AHS Adaptive Structures Forum 曲线。结果表明,该方法能够模拟出反作用轮干扰 AIAA Forum on Non-Deterministric Approaches Con- 力作为微振动激励源频率高、幅值低的特性,并且不 ference.St.Louis Missouri:[s.n.].1999. 需要复杂的实验测试,简便高效,适用性强。 [7]Gregory W N,James W M.Vibration attenuation ap- proach for spaceborne optical interferometers [J]. 参考文献 Transactions on Control System Technology,1998.6 (6):689-700. [1]张振华,杨雷,庞世伟.高精度航天器微振动力学环境 [8]朱位秋.随机振动[M].北京:科学出版社,1992:7- 分析[J门.航天器环境工程,2009,6(26):528-534. 52. Zhang Zhenhua,Yang Lei,Pang Shiwei.Jitter envi- [9]胡隶贤.地震工程学[M].2版.北京:地震出版社, 2006:41-45. ronment analysis for micro-precision spacecraft [J]. Space Environment Engineering.2009.6(26):528-534. [10]徐赵东.土木工程常用软件分析与应用[们.北京:中 国建筑工业出版社,2010:112-141. (in Chinese) [11]王济.MATLAB在振动信号处理中的应用[M].北 [2]Rahman Z H.Laskin R A.Multi-axis vibration isola- 京:中国水利水电出版社,2006:149-152. tion suppression and steering system for space obser- vational applications[C]//Proceedings of the Interna- tional Society for Optical Engineering.Kona.HI: 第一作者简介:徐赵东,男,1975年11 Telescope Control SystemsⅢ,1998:73-83. 月生,教授、博士生导师。主要研究方向 [3] Bialke B.A compilation of reaction wheel induced 为结构振动控制与动力学,结构抗震,智 spacecraft disturbances [C]/20th Annual American 能材料与结构。曾发表《Horizontal sha-. Aeronautical Society Guidance and Control Confer- king table tests on structures using in- ence.San Diego,CA:[s.n.].1997. norative》?(《Journal of Sound and Vibra- [4]Eric H A,John P F.Erwin R S.Satellite ultraquiet i- tion》2009,Vol.325,No.(1-2)等 solation technology[C]//IEEE Aerospace Conference. 论文。 Montana:[s.n.].2005. E-mail:xuzhdgyg@seu.edu.cn
6 结束语 为了保证高精度航天器的有效载荷在微振动力 学环境下良好的工作性能,反作用轮干扰力作为主 要的激励源,对其特性的研究分析有助于高精度航 天器 隔 减 振 系 统 的 评 估 分 析。笔 者 以 IthacoB wheel测试实验为背景进行数据模拟,在反作用轮 干扰力经典线性稳态模型的基础上,对其参数进行 识别,推导了反作用轮干扰力的功率谱密度函数,并 用修正的傅里叶谱法模拟了反作用轮干扰力的时程 曲线。结果表明,该方法能够模拟出反作用轮干扰 力作为微振动激励源频率高、幅值低的特性,并且不 需要复杂的实验测试,简便高效,适用性强。 参 考 文 献 [1] 张振华,杨雷,庞世伟.高精度航天器微振动力学环境 分析[J].航天器环境工程,2009,6(26):528534. ZhangZhenhua,YangLei,PangShiwei.Jitterenvi ronmentanalysisfor microprecisionspacecraft [J]. SpaceEnvironmentEngineering,2009,6(26):528534. (inChinese) [2] RahmanZH,LaskinRA.Multiaxisvibrationisola tionsuppressionandsteeringsystemforspaceobser vationalapplications[C]∥ProceedingsoftheInterna tionalSocietyfor Optical Engineering.Kona, HI: TelescopeControlSystemsⅢ,1998:7383. [3] Bialke B.A compilation ofreaction wheelinduced spacecraftdisturbances[C]∥20th AnnualAmerican AeronauticalSociety Guidance and Control Confer ence.SanDiego,CA:[s.n.],1997. [4] EricH A,JohnPF,ErwinRS.Satelliteultraquieti solationtechnology[C]∥IEEEAerospaceConference. Montana:[s.n.],2005. [5] 皮阳军,王宣银,罗晓晔,等.六自由度舰船运动模拟 器随机海浪 谱 模 拟 [J].振 动、测 试 与 诊 断,2010,4 (30):375378. PiYangjun,WangXuanyin,LuoXiaoye,etal.Simu lationtorandom ocean wavespectrum usingsixde greesoffreedomshipmotionsimulator[J].Journalof Vibration,Measure & Diagnosis,2010,4(30):375 378.(inChinese) [6] RebeccaA M,DavidW M,RobertLG.Development ofempiricalandanalyticalreaction wheeldisturbance models[C]∥40th AIAA/ASCE/AHS/ASC Struc tures,StructuralDynamicsand MaterialsConference. AIAA/ASME/AHS Adaptive Structures Forum AIAAForumonNonDeterministricApproachesCon ference.St.LouisMissouri:[s.n.],1999. [7] GregoryW N,JamesW M.Vibrationattenuationap proachfor spaceborne opticalinterferometers[J]. TransactionsonControlSystem Technology,1998,6 (6):689700. [8] 朱位秋.随机振动[M].北京:科学出版 社,1992:7 52. [9] 胡隶贤.地震工程学[M].2版.北京:地震出版 社, 2006:4145. [10]徐赵东.土木工程常用软件分析与应用[M].北京:中 国建筑工业出版社,2010:112141. [11]王济.MATLAB在振动信号处理中 的 应 用[M].北 京:中 国水利水电出版社,2006:149152. 第一作 者 简 介:徐 赵 东,男,1975 年 11 月生,教授、博士生导师。主要研究方向 为结构振动控制与动力学、结构抗震、智 能材料与结构。曾发表《Horizontalsha kingtabletestsonstructuresusingin norative》(《JournalofSoundandVibra tion》2009, Vol.325, No.(12))等 论文。 Email:xuzhdgyq@seu.edu.cn 第5期 徐赵东,等:航天器中反作用轮干扰力仿真研究 885