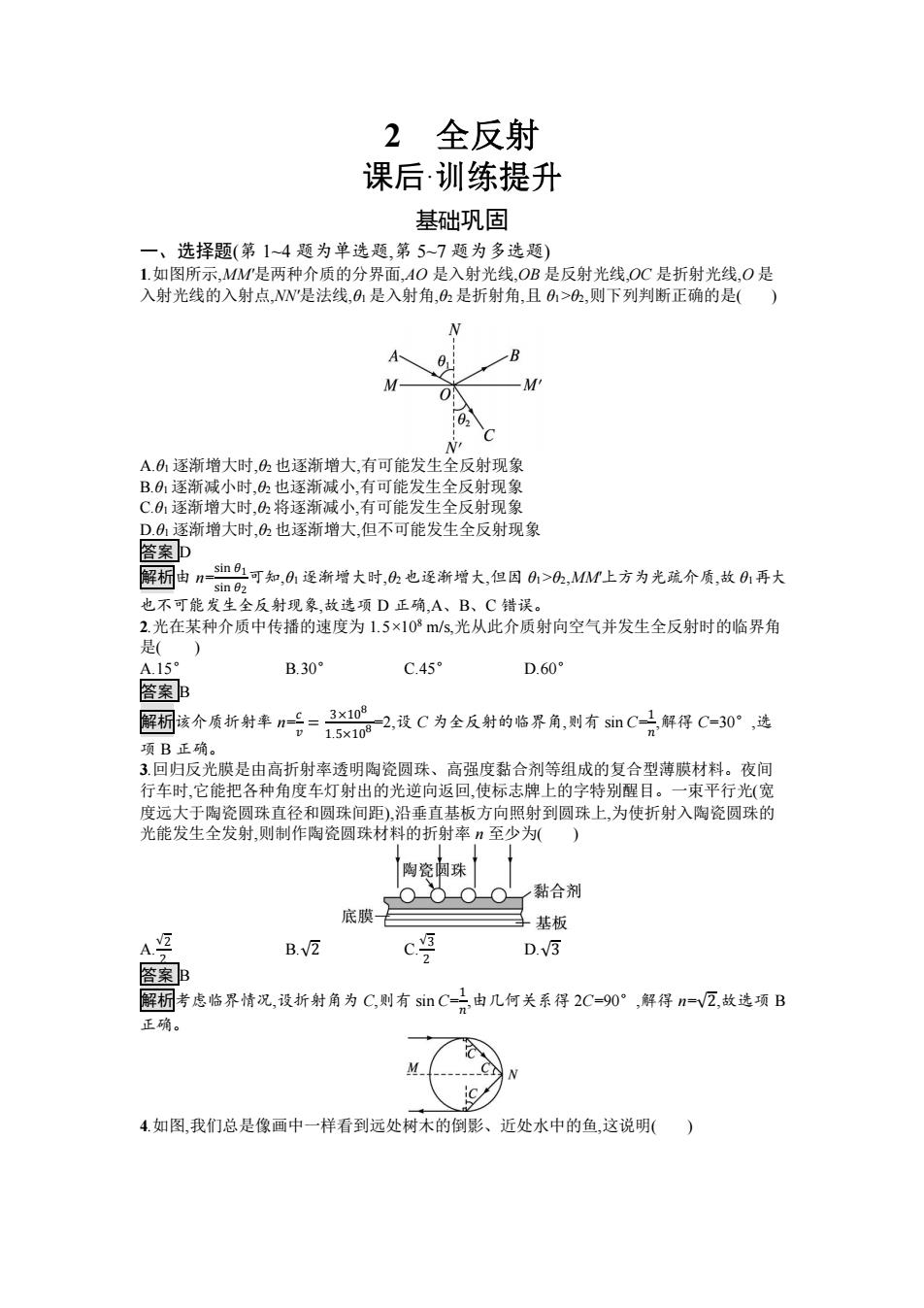
2全反射 课后·训练提升 基础巩固 一、选择题(第1~4题为单选题,第5~7题为多选题) 1.如图所示,MM是两种介质的分界面,AO是入射光线,OB是反射光线,OC是折射光线,O是 入射光线的入射点,NN是法线,0是入射角,2是折射角,且0>,则下列判断正确的是() M 02N N A.01逐渐增大时,也逐渐增大,有可能发生全反射现象 B.01逐渐减小时,也逐渐减小,有可能发生全反射现象 C.01逐渐增大时,将逐渐减小,有可能发生全反射现象 D.0逐渐增大时,凸也逐渐增大,但不可能发生全反射现象 答案D 解杨由nm8可知,0逐渐增大时,也逐渐增大,但因>,MM上方为光疏介质,故01再大 sin 02 也不可能发生全反射现象,故选项D正确,A、B、C错误。 2.光在某种介质中传播的速度为1.5×108m/s.光从此介质射向空气并发生全反射时的临界角 是() A.15° B.30° C.45° D.60° 客案B 解桐该介质折射率n 5x1092,设C为全反射的临界角,则有sinC解得C=30°,选 -3×108 项B正确。 3.回归反光膜是由高折射率透明陶瓷圆珠、高强度黏合剂等组成的复合型薄膜材料。夜间 行车时,它能把各种角度车灯射出的光逆向返回,使标志牌上的字特别醒目。一束平行光(宽 度远大于陶瓷圆珠直径和圆珠间距),沿垂直基板方向照射到圆珠上,为使折射入陶瓷圆珠的 光能发生全发射,则制作陶瓷圆珠材料的折射率n至少为( 陶瓷圆珠 黏合剂 底膜 基板 A马 B.2 c D.3 答案B 解韧考虑临界情况,设折射角为C则有snC品由几何关系得2C-90°,解得m=V巨,故选项B 正确。 4.如图,我们总是像画中一样看到远处树木的倒影、近处水中的鱼,这说明()
2 全反射 课后· 基础巩固 一、选择题(第 1~4 题为单选题,第 5~7 题为多选题) 1.如图所示,MM'是两种介质的分界面,AO 是入射光线,OB 是反射光线,OC 是折射光线,O 是 入射光线的入射点,NN'是法线,θ1 是入射角,θ2 是折射角,且 θ1>θ2,则下列判断正确的是( ) A.θ1 逐渐增大时,θ2 也逐渐增大,有可能发生全反射现象 B.θ1 逐渐减小时,θ2 也逐渐减小,有可能发生全反射现象 C.θ1 逐渐增大时,θ2 将逐渐减小,有可能发生全反射现象 D.θ1 逐渐增大时,θ2 也逐渐增大,但不可能发生全反射现象 答案 D 解析由 n= sin 𝜃1 sin 𝜃2 可知,θ1 逐渐增大时,θ2 也逐渐增大,但因 θ1>θ2,MM'上方为光疏介质,故 θ1再大 也不可能发生全反射现象,故选项 D 正确,A、B、C 错误。 2.光在某种介质中传播的速度为 1.5×108 m/s,光从此介质射向空气并发生全反射时的临界角 是( ) A.15° B.30° C.45° D.60° 答案 B 解析该介质折射率 n= 𝑐 𝑣 = 3×10 8 1.5×10 8=2,设 C 为全反射的临界角,则有 sin C=1 𝑛 ,解得 C=30°,选 项 B 正确。 3.回归反光膜是由高折射率透明陶瓷圆珠、高强度黏合剂等组成的复合型薄膜材料。夜间 行车时,它能把各种角度车灯射出的光逆向返回,使标志牌上的字特别醒目。一束平行光(宽 度远大于陶瓷圆珠直径和圆珠间距),沿垂直基板方向照射到圆珠上,为使折射入陶瓷圆珠的 光能发生全发射,则制作陶瓷圆珠材料的折射率 n 至少为( ) A. √2 2 B.√2 C. √3 2 D.√3 答案 B 解析考虑临界情况,设折射角为 C,则有 sin C=1 𝑛 ,由几何关系得 2C=90°,解得 n=√2,故选项 B 正确。 4.如图,我们总是像画中一样看到远处树木的倒影、近处水中的鱼,这说明( )

A.远处水中没有鱼 B.树木倒影是树木反射的光先进入水中,然后再通过水的折射进入人的眼中 C近处的鱼反射的光入射角大,容易发生全反射 D.远处的鱼反射的光入射角大,容易发生全反射 答案D 解析远处的鱼反射的光入射角较大,当入射角大于等于全反射临界角时发生全反射,光线不 能射出水面,所以看不到,故选项D正确,A、C错误。树木倒影是树木反射的光在水面发生 反射后,反射光进入人的眼中,故选项B错误。 5.光导纤维是由内芯和外套两层组成,光从一端进入,另一端传出。下列说法正确的是() 端面 一外套 空气 内芯 A.内芯的折射率大于外套的折射率 B.增大光从端面入射的入射角,在端面处可能发生全反射 C.不同频率的可见光从同一根光导纤维的一端传输到另一端所用的时间不相同 D.若红光以如图所示的角度入射,恰能在内芯和外套界面上发生全反射,则改用紫光以同样角 度入射时,在内芯和外套界面上将不会发生全反射 答案AC 解桐光导纤维传递光信号是利用光的全反射原理,所以内芯的折射率大于外套的折射率,在 端面不可能发生全反射,故选项A正确,B错误。根据v=可知,不同频率的可见光在同一介 质中折射率不同,传播速度不同,故所用时间也不同,故选项C正确。红光临界角大于紫光临 界角,红光恰能发生全反射,紫光更能发生全反射,故选项D错误。 6如图所示,一束蓝光从空气垂直入射到直角三棱镜的BC面上,已知∠A=30°,蓝光从棱镜到 空气全反射的临界角为45°,则( A该直角三棱镜对蓝光的折射率为v2 B该直角三棱镜对蓝光的折射率为号 C.蓝光第一次从棱镜射入空气时的折射角为45° D.蓝光第一次从棱镜射入空气时的折射角为60° 答案AC 解杨据全反射临界角公式sC-得,折射率n=V2,故选项A正确,B错误。光路图如图所示, 因为i1=60°>C,所以光线在AB面上将发生全反射。由几何知识得i2=i1-30°=30°<C,则 光钱从4C面上第一次射入空气。由折射定律有川品可得45”,即宝光第一次从校镜 射入空气时的折射角为45°,故选项C正确,D错误
A.远处水中没有鱼 B.树木倒影是树木反射的光先进入水中,然后再通过水的折射进入人的眼中 C.近处的鱼反射的光入射角大,容易发生全反射 D.远处的鱼反射的光入射角大,容易发生全反射 答案 D 解析远处的鱼反射的光入射角较大,当入射角大于等于全反射临界角时发生全反射,光线不 能射出水面,所以看不到,故选项 D 正确,A、C 错误。树木倒影是树木反射的光在水面发生 反射后,反射光进入人的眼中,故选项 B 错误。 5.光导纤维是由内芯和外套两层组成,光从一端进入,另一端传出。下列说法正确的是( ) A.内芯的折射率大于外套的折射率 B.增大光从端面入射的入射角,在端面处可能发生全反射 C.不同频率的可见光从同一根光导纤维的一端传输到另一端所用的时间不相同 D.若红光以如图所示的角度入射,恰能在内芯和外套界面上发生全反射,则改用紫光以同样角 度入射时,在内芯和外套界面上将不会发生全反射 答案 AC 解析光导纤维传递光信号是利用光的全反射原理,所以内芯的折射率大于外套的折射率,在 端面不可能发生全反射,故选项 A 正确,B 错误。根据 v= 𝑐 𝑛可知,不同频率的可见光在同一介 质中折射率不同,传播速度不同,故所用时间也不同,故选项 C 正确。红光临界角大于紫光临 界角,红光恰能发生全反射,紫光更能发生全反射,故选项 D 错误。 6.如图所示,一束蓝光从空气垂直入射到直角三棱镜的 BC 面上,已知∠A=30°,蓝光从棱镜到 空气全反射的临界角为 45°,则( ) A.该直角三棱镜对蓝光的折射率为√2 B.该直角三棱镜对蓝光的折射率为√2 2 C.蓝光第一次从棱镜射入空气时的折射角为 45° D.蓝光第一次从棱镜射入空气时的折射角为 60° 答案 AC 解析据全反射临界角公式 sin C=1 𝑛得,折射率 n=√2,故选项 A 正确,B 错误。光路图如图所示, 因为 i1=60°>C,所以光线在 AB 面上将发生全反射。由几何知识得 i2=i1-30°=30°<C,则 光线从 AC 面上第一次射入空气。由折射定律有 n= sin𝑟 sin 𝑖2 ,可得 r=45°,即蓝光第一次从棱镜 射入空气时的折射角为 45°,故选项 C 正确,D 错误

60 7.右图是一横截面为直角三角形的玻璃三棱柱,∠C=30°。现有一细束光线沿着截面从AC 边上的O点以45°的入射角射入,折射后到达斜边BC发生反射,最后垂直AB界面射出。则 () C30 0 45 A透明玻璃材料的折射率为2 B.透明玻璃材料的全反射临界角为45° C.光线在BC界面的入射角为30° D.光线在BC界面发生全反射 答案BD 解析画出光路图如图所示,由图中几何关系可知光线在AC界面折射角r=30°,由折射定律 n巴解得m=厄故选项A错误。由smC可得,全反射临界角为C-45”,故选项B正 确。根据图中平面几何关系,BC界面入射角为'=60°,故选项C错误。由于1>45°,所以光 线在BC界面发生全反射,故选项D正确。 30 0 459 二、非选择题 8.一足够大的水池内盛有某种透明液体,液体的深度为h,在水池的底部放一点光源S,其中一 条光线以30°入射角射到液体与空气的分界面上,它的反射光线与折射光线的夹角为90°, 如图所示。求: (1)液体的折射率: (2)液体表面亮斑的面积。 答案1)W3(2)2 解析1)由几何关系得r=180°-30°-90°=60 则n晋=V3。 2)因为sinC-1=9 3 剥mc号 则亮斑半径R 21 亮斑面积S=πR2r
7.右图是一横截面为直角三角形的玻璃三棱柱,∠C=30°。现有一细束光线沿着截面从 AC 边上的 O 点以 45°的入射角射入,折射后到达斜边 BC 发生反射,最后垂直 AB 界面射出。则 ( ) A.透明玻璃材料的折射率为 2 B.透明玻璃材料的全反射临界角为 45° C.光线在 BC 界面的入射角为 30° D.光线在 BC 界面发生全反射 答案 BD 解析画出光路图如图所示,由图中几何关系可知光线在 AC 界面折射角 r=30°,由折射定律 n= sin𝑖 sin𝑟 ,解得 n=√2,故选项 A 错误。由 sin C=1 𝑛 可得,全反射临界角为 C=45°,故选项 B 正 确。根据图中平面几何关系,BC 界面入射角为 i'=60°,故选项 C 错误。由于 i'>45°,所以光 线在 BC 界面发生全反射,故选项 D 正确。 二、非选择题 8.一足够大的水池内盛有某种透明液体,液体的深度为 h,在水池的底部放一点光源 S,其中一 条光线以 30°入射角射到液体与空气的分界面上,它的反射光线与折射光线的夹角为 90°, 如图所示。求: (1)液体的折射率; (2)液体表面亮斑的面积。 答案(1)√3 (2)1 2 πh 2 解析(1)由几何关系得 r=180°-30°-90°=60° 则 n= sin𝑟 sin𝑖 = √3。 (2)因为 sin C=1 𝑛 = √3 3 则 tan C=√2 2 则亮斑半径 R=√2 2 h 亮斑面积 S=πR 2= 1 2 πh 2
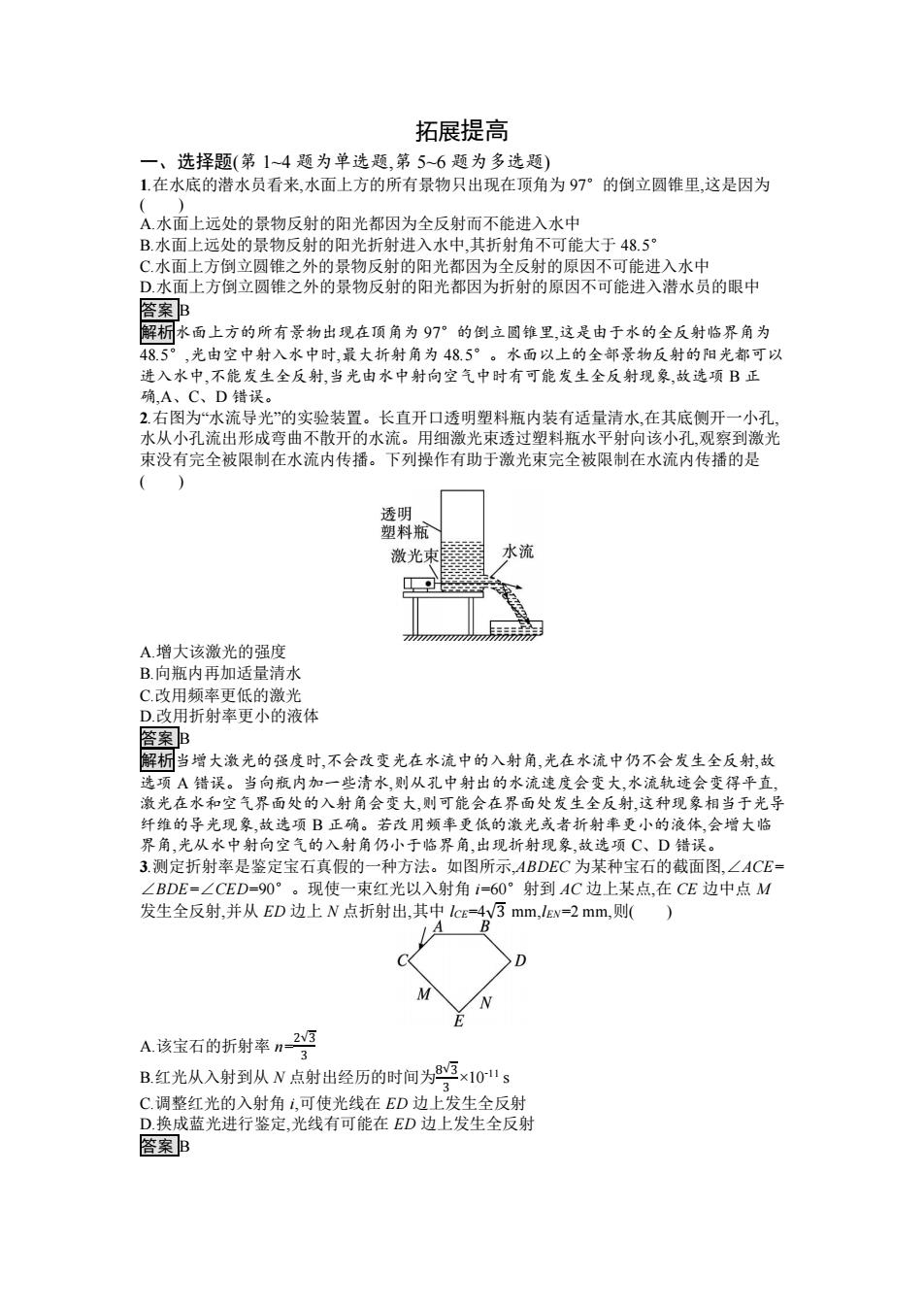
拓展提高 一、选择题(第14题为单选题,第5~6题为多选题) 1在水底的潜水员看来,水面上方的所有景物只出现在顶角为97°的倒立圆锥里,这是因为 A水面上远处的景物反射的阳光都因为全反射而不能进入水中 B.水面上远处的景物反射的阳光折射进入水中.其折射角不可能大于48.5° C.水面上方倒立圆锥之外的景物反射的阳光都因为全反射的原因不可能进入水中 D.水面上方倒立圆锥之外的景物反射的阳光都因为折射的原因不可能进入潜水员的眼中 客案B 解析水面上方的所有景物出现在顶角为97°的倒立圆锥里,这是由于水的全反射临界角为 48.5°,光由空中射入水中时,最大折射角为48.5°。水面以上的全部景物反射的阳光都可以 进入水中,不能发生全反射,当光由水中射向空气中时有可能发生全反射现象,故选项B正 确,A、C、D错误。 2.右图为水流导光”的实验装置。长直开口透明塑料瓶内装有适量清水,在其底侧开一小孔, 水从小孔流出形成弯曲不散开的水流。用细激光束透过塑料瓶水平射向该小孔,观察到激光 束没有完全被限制在水流内传播。下列操作有助于激光束完全被限制在水流内传播的是 透明 塑料瓶 激光束 A.增大该激光的强度 B.向瓶内再加适量清水 C.改用频率更低的激光 D.改用折射率更小的液体 答案B 解析当增大激光的强度时,不会改变光在水流中的入射角,光在水流中仍不会发生全反射,故 选项A错误。当向瓶内加一些清水,则从孔中射出的水流速度会变大,水流轨迹会变得平直 激光在水和空气界面处的入射角会变大,则可能会在界面处发生全反射,这种现象相当于光导 纤维的导光现象,故选项B正确。若改用频率更低的激光或者折射率更小的液体,会增大临 界角,光从水中射向空气的入射角仍小于临界角,出现折射现象,故选项C、D错误。 3.测定折射率是鉴定宝石真假的一种方法。如图所示,ABDEC为某种宝石的截面图,∠ACE= ∠BDE=∠CED=90°。现使一束红光以入射角i=60°射到AC边上某点,在CE边中点M 发生全反射,并从ED边上N点折射出,其中lcE=4V3mm,lEv=2mm,则() A.该宝石的折射率n23 3 B红光从入射到从N点射出经历的时间为3×101s 2 C.调整红光的入射角,可使光线在ED边上发生全反射 D.换成蓝光进行鉴定,光线有可能在ED边上发生全反射 答案B
拓展提高 一、选择题(第 1~4 题为单选题,第 5~6 题为多选题) 1.在水底的潜水员看来,水面上方的所有景物只出现在顶角为 97°的倒立圆锥里,这是因为 ( ) A.水面上远处的景物反射的阳光都因为全反射而不能进入水中 B.水面上远处的景物反射的阳光折射进入水中,其折射角不可能大于 48.5° C.水面上方倒立圆锥之外的景物反射的阳光都因为全反射的原因不可能进入水中 D.水面上方倒立圆锥之外的景物反射的阳光都因为折射的原因不可能进入潜水员的眼中 答案 B 解析水面上方的所有景物出现在顶角为 97°的倒立圆锥里,这是由于水的全反射临界角为 48.5°,光由空中射入水中时,最大折射角为 48.5°。水面以上的全部景物反射的阳光都可以 进入水中,不能发生全反射,当光由水中射向空气中时有可能发生全反射现象,故选项 B 正 确,A、C、D 错误。 2.右图为“水流导光”的实验装置。长直开口透明塑料瓶内装有适量清水,在其底侧开一小孔, 水从小孔流出形成弯曲不散开的水流。用细激光束透过塑料瓶水平射向该小孔,观察到激光 束没有完全被限制在水流内传播。下列操作有助于激光束完全被限制在水流内传播的是 ( ) A.增大该激光的强度 B.向瓶内再加适量清水 C.改用频率更低的激光 D.改用折射率更小的液体 答案 B 解析当增大激光的强度时,不会改变光在水流中的入射角,光在水流中仍不会发生全反射,故 选项 A 错误。当向瓶内加一些清水,则从孔中射出的水流速度会变大,水流轨迹会变得平直, 激光在水和空气界面处的入射角会变大,则可能会在界面处发生全反射,这种现象相当于光导 纤维的导光现象,故选项 B 正确。若改用频率更低的激光或者折射率更小的液体,会增大临 界角,光从水中射向空气的入射角仍小于临界角,出现折射现象,故选项 C、D 错误。 3.测定折射率是鉴定宝石真假的一种方法。如图所示,ABDEC 为某种宝石的截面图,∠ACE= ∠BDE=∠CED=90°。现使一束红光以入射角 i=60°射到 AC 边上某点,在 CE 边中点 M 发生全反射,并从 ED 边上 N 点折射出,其中 lCE=4√3 mm,lEN=2 mm,则( ) A.该宝石的折射率 n= 2√3 3 B.红光从入射到从 N 点射出经历的时间为8√3 3 ×10-11 s C.调整红光的入射角 i,可使光线在 ED 边上发生全反射 D.换成蓝光进行鉴定,光线有可能在 ED 边上发生全反射 答案 B

解析作出光线传播光路如图所示,设光线在AC边的折射角为B,由几何关系可知∠EMN=B 故m=品=票所以月-30,该宝石的折射率州器=V3故选项A错误。根据先 的传播规律,可得红光在钻石中传播的速度大小为v-=V3×I08ms,由几何关系可知,光在 钻石中走过的路程为s=pM+l=4mm+4mm=8×I03m,可得光在钻石中传搐的时间1号= 8x103×101s,故选项B正确。根据以上分析可知,国为在P点的折射角等于在ED边 3x108s=3 上的入射角,根据光路可逆性原理可知,一定不会在ED边发生全反射,故选项C、D错误。 4.截面为等腰直角三角形的棱镜叫全反射棱镜,这种棱镜在光学仪器中广泛用于改变光的传 播方向。如图所示,一束宽度为I的单色平行光束射向全反射棱镜AC面的AP部分,光束平 行于AB面入射,由P点入射的光线恰好射到B点,光线经AB面发生一次全反射后从BC面 射出。已知棱镜对该光的折射率为n=-V2,光在真空中的传播速度为c,sn15°严,则 4 () A.光在棱镜中的传播速度为√2c B.光在棱镜中发生全反射的临界角为30° C.从BC面出射的光,在棱镜中的传播时间均为3+1型 D光束从BC面出射后仍平行,宽度变为受 答案 图团光在棱镜中的传播速度为片-号选项A错误。设光在校镜中发生金反射的临界角 为0则sm0片-号回光光在棱镜中发生全反射的临界角为45°,选项B错误。由几有关系 可得=V2由光的折射定律可得n由于入射角45°,可得-30°,则∠PBA=15°, 由正孩定理可得丽=m解得B6+V2L由几何关系可得,BC面出射的光在棱 LAP 镜中的传播距离均等于,从BC面出射的光,在棱镜中的传播时间均为1胆=6+型= 1 2+业选项C正确。光束平行于AB面入射,由P点入射的光线恰好射到B点,光线经AB 面发生一次全反射后从BC面射出,由几何关系可得,光束在BC面的入射角'=30°,由光的 折射定律可得n晋解得r45°,国北光束从BC面出射后仍与AB平行,由对称性可得,宽 度仍为I,选项D错误。 5.如图所示,储油桶的底面直径与高均为d。当桶内没有油时,从某点A恰能看到桶底边缘的 点B。当桶内装满油时,仍沿AB方向看去,恰好看到桶底上的点C,C、B两点相距二。光在空 气中的传播速度可视为真空中的光速c。则(
解析作出光线传播光路如图所示,设光线在 AC 边的折射角为 β,由几何关系可知∠EMN=β, 故 tan β= 𝑙𝐸𝑁 𝑙𝐸𝑀 = 2 2√3 = √3 3 ,所以 β=30°,该宝石的折射率 n= sin𝛼 sin𝛽 = √3,故选项 A 错误。根据光 的传播规律,可得红光在钻石中传播的速度大小为 v= 𝑐 𝑛 = √3×108 m/s,由几何关系可知,光在 钻石中走过的路程为 s=lPM+lMN=4 mm+4 mm=8×10-3 m,可得光在钻石中传播的时间 t= 𝑠 𝑣 = 8×10 -3 √3×10 8 s= 8√3 3 ×10-11 s,故选项 B 正确。根据以上分析可知,因为在 P 点的折射角等于在 ED 边 上的入射角,根据光路可逆性原理可知,一定不会在 ED 边发生全反射,故选项 C、D 错误。 4.截面为等腰直角三角形的棱镜叫全反射棱镜,这种棱镜在光学仪器中广泛用于改变光的传 播方向。如图所示,一束宽度为 l 的单色平行光束射向全反射棱镜 AC 面的 AP 部分,光束平 行于 AB 面入射,由 P 点入射的光线恰好射到 B 点,光线经 AB 面发生一次全反射后从 BC 面 射出。已知棱镜对该光的折射率为 n=√2,光在真空中的传播速度为 c,sin 15°= √6-√2 4 ,则 ( ) A.光在棱镜中的传播速度为√2c B.光在棱镜中发生全反射的临界角为 30° C.从 BC 面出射的光,在棱镜中的传播时间均为2(√3+1)𝑙 𝑐 D.光束从 BC 面出射后仍平行,宽度变为√2 2 l 答案 C 解析光在棱镜中的传播速度为 v= 𝑐 𝑛 = √2 2 c,选项 A 错误。设光在棱镜中发生全反射的临界角 为 θ,则 sin θ= 1 𝑛 = √2 2 ,因此光在棱镜中发生全反射的临界角为 45°,选项 B 错误。由几何关系 可得 lAP=√2l,由光的折射定律可得 n= sin𝑖 sin𝑟 ,由于入射角 i=45°,可得 r=30°,则∠PBA=15°, 由正弦定理可得 𝑙𝑃𝐵 sin∠𝑃𝐴𝐵 = 𝑙𝐴𝑃 sin∠𝑃𝐵𝐴,解得 lPB=(√6 + √2)l,由几何关系可得,BC 面出射的光在棱 镜中的传播距离均等于 lPB;从 BC 面出射的光,在棱镜中的传播时间均为 t= 𝑙𝑃𝐵 𝑣 = (√6+√2)𝑙 √2 2 𝑐 = 2(√3+1)𝑙 𝑐 ,选项 C 正确。光束平行于 AB 面入射,由 P 点入射的光线恰好射到 B 点,光线经 AB 面发生一次全反射后从 BC 面射出,由几何关系可得,光束在 BC 面的入射角 i'=30°,由光的 折射定律可得 n= sin𝑟' sin𝑖' ,解得 r'=45°,因此光束从 BC 面出射后仍与 AB 平行,由对称性可得,宽 度仍为 l,选项 D 错误。 5.如图所示,储油桶的底面直径与高均为 d。当桶内没有油时,从某点 A 恰能看到桶底边缘的 点 B。当桶内装满油时,仍沿 AB 方向看去,恰好看到桶底上的点 C,C、B 两点相距𝑑 3。光在空 气中的传播速度可视为真空中的光速 c。则( )

A.桶内油的折射率为2西 13 B.桶内油的折射率为匹 4 C光在桶内油中传播的速度为2匹。 13℃ D.来自C点的光射向油面时一定会出现全反射现象 答案BC 解韧由题意可知,没有油时,到达B点光线的入射角的正切为tan0-是l,即0a=45° 当装满油时,到达C点的光线的折射角的正切为 如4-号 利用数学知识,求得sin,=三s 2,sin6-2☒ 13 桶内尚的折射率为川品=要故选项A错误,B正确。 sin 02 根据后求得,故选项C正确。 当桶内装满油时,仍从AB方向看去,恰好看到桶底的,点C,可知光从C点射向油面时一定不会 出现全反射现象,故选项D错误。 6.某长方体透明介质如图所示。e为嵌在介质内部紧贴ddc'c面的线状单色可见光光源,ef 与abcd面垂直,e为dc中点,lab=2lbc。介质对该单色光的折射率为2,只考虑由ef直接射向面 aa'b'b的光线。下列说法正确的是( A光从aabb面出射的区域占该面总面积的 B,光从0bb面出射的区域占该面总面积的 C.若ef发出的单色光频率变小,aa'b'b面有光出射的区域面积将增大 D.若ef发出的单色光频率变小,aa'b'b面有光出射的区域面积将减小 答案AC 解粉从光源发出的光射到aabb面上的临界角满足sinC-号=影解得C-30° 设lab-2le=2L,则在aa'bb面上有光线射出的长度为x=2han30°2y3 3 234 则有光线射出的面积占该面总面积的比例为如 _三选项A正确,B错误。 2=32 若ef发出的单色光频率变小,则光的折射率变小,临界角变大,根据x=2tanC,则在aa'b'b面上 有光线射出的长度变大,则aa'b'b面有光出射的区域面积将增大,选项C正确,D错误。 二、非选择题 7.如图所示,4AOB是由某种透明物质制成的圆柱体横截面(0为圆心),折射率为V2。今有一 束平行光以45°的入射角射向柱体的OA平面,这些光线中有一部分不能从柱体的AB面上 射出。设凡射到OB面的光线全部被吸收,也不考虑OA面的反射,求圆柱AB面上能射出光 线的部分占AB表面的比例
A.桶内油的折射率为2√26 13 B.桶内油的折射率为√26 4 C.光在桶内油中传播的速度为2√26 13 c D.来自 C 点的光射向油面时一定会出现全反射现象 答案 BC 解析由题意可知,没有油时,到达 B 点光线的入射角的正切为 tan θ1= 𝑑 𝑑 =1,即 θ1=45° 当装满油时,到达 C 点的光线的折射角的正切为 tan θ2= 𝑑- 𝑑 3 𝑑 = 2 3 利用数学知识,求得 sin θ1= √2 2 ,sin θ2= 2√13 13 桶内油的折射率为 n= sin 𝜃1 sin 𝜃2 = √26 4 ,故选项 A 错误,B 正确。 根据 v= 𝑐 𝑛 ,求得 v= 2√26 13 c,故选项 C 正确。 当桶内装满油时,仍从 AB 方向看去,恰好看到桶底的点 C,可知光从 C 点射向油面时一定不会 出现全反射现象,故选项 D 错误。 6.某长方体透明介质如图所示。ef 为嵌在介质内部紧贴 dd'c'c 面的线状单色可见光光源,ef 与 abcd 面垂直,e 为 dc 中点,lab=2lbc。介质对该单色光的折射率为 2,只考虑由 ef 直接射向面 aa'b'b 的光线。下列说法正确的是( ) A.光从 aa'b'b 面出射的区域占该面总面积的√3 3 B.光从 aa'b'b 面出射的区域占该面总面积的√3 6 C.若 ef 发出的单色光频率变小,aa'b'b 面有光出射的区域面积将增大 D.若 ef 发出的单色光频率变小,aa'b'b 面有光出射的区域面积将减小 答案 AC 解析从光源发出的光射到 aa'b'b 面上的临界角满足 sin C=1 𝑛 = 1 2 ,解得 C=30° 设 lab=2lbc=2l,则在 aa'b'b 面上有光线射出的长度为 x=2ltan 30°= 2√3𝑙 3 则有光线射出的面积占该面总面积的比例为𝑙𝑏𝑏' · 2√3𝑙 3 𝑙𝑏𝑏' ·2𝑙 = √3 3 ,选项 A 正确,B 错误。 若 ef 发出的单色光频率变小,则光的折射率变小,临界角变大,根据 x=2ltan C,则在 aa'b'b 面上 有光线射出的长度变大,则 aa'b'b 面有光出射的区域面积将增大,选项 C 正确,D 错误。 二、非选择题 7.如图所示,AOB 是由某种透明物质制成的1 4圆柱体横截面(O 为圆心),折射率为√2。今有一 束平行光以 45°的入射角射向柱体的 OA 平面,这些光线中有一部分不能从柱体的 AB 面上 射出。设凡射到 OB 面的光线全部被吸收,也不考虑 OA 面的反射,求圆柱 AB 面上能射出光 线的部分占 AB 表面的比例

挡光板 0 B A 挡光板 答刻 解析光路图如图所示。 挡光板 450 B 挡光板 设从0点射入的光线,折射角为根据折射定律,有n二,解得一30 设从某位置P点入射的光线,折射到AB孤面上的Q点时,入射角恰等于临界角C,有sC是 代入数据得C=45 △PQ0中,a=180°-90°-C-r=15° 所以能射出光线的区域对应的圆心角B=90°-Q-r=45 能射出光线的部分占AB面的比例为5:: 1 90°=20 挑战创新 下图是一个半球形透明物体放在真空中的侧视图,现在有一细束单色光沿半径OA方向入射, 保持入射方向不变,不考虑光线在透明物体内部的反射。 R (1)将细光束平移到距0点号R处的C点此时透明体左侧怡好不再有光线射出,求透明体对 该单色光的折射率。 (2)若细光束平移到距O点0.5R处,已知光在真空中的传播速度为c,求该细光束从开始进入 透明体到折射到OA轴线上的时间。 答案1)V3(2) 5R 解析1)如图所示,光束由C处水平射入在B处发生全反射,∠OBC为临界角。 B sin∠oBcc==3 loB 3 由临界角公式得nn20Bc=V3。 (2)如图所示,光束由D,点水平射入,在E点发生折射
答案1 2 解析光路图如图所示。 设从 O 点射入的光线,折射角为 r,根据折射定律,有 n= sin45° sin𝑟 ,解得 r=30° 设从某位置 P 点入射的光线,折射到 AB 弧面上的 Q 点时,入射角恰等于临界角 C,有 sin C=1 𝑛 , 代入数据得 C=45° △PQO 中,α=180°-90°-C-r=15° 所以能射出光线的区域对应的圆心角 β=90°-α-r=45° 能射出光线的部分占 AB 面的比例为 45° 90° = 1 2 。 挑战创新 下图是一个半球形透明物体放在真空中的侧视图,现在有一细束单色光沿半径 OA 方向入射, 保持入射方向不变,不考虑光线在透明物体内部的反射。 (1)将细光束平移到距 O 点 √3 3 R 处的 C 点,此时透明体左侧恰好不再有光线射出,求透明体对 该单色光的折射率。 (2)若细光束平移到距 O 点 0.5R 处,已知光在真空中的传播速度为 c,求该细光束从开始进入 透明体到折射到 OA 轴线上的时间。 答案(1) √3 (2) 5𝑅 2𝑐 解析(1)如图所示,光束由 C 处水平射入,在 B 处发生全反射,∠OBC 为临界角。 sin ∠OBC=𝑙𝑂𝐶 𝑙𝑂𝐵 = √3 3 𝑅 𝑅 = √3 3 由临界角公式得 n= 1 sin∠𝑂𝐵𝐶 = √3。 (2)如图所示,光束由 D 点水平射入,在 E 点发生折射

N-- B AG 设入射角为∠OED=Q,折射角为∠NEF=B,则折射率n-s加E=V3 sina 部_1 由几何关系可知sina-R=2a=30 2f=60° 以上两式联立,解得snB 由几何关系可知∠FOE=a=30°,∠OFE=B-a=30°,故lEF=R D点到E点的时间1一兰=元 E点到F点的时间2 R 细光泉从开拾进入连明体到折射到OA轴钱上的时间+北器
设入射角为∠OED=α,折射角为∠NEF=β,则折射率 n= sin𝛽 sin𝛼 = √3 由几何关系可知 sin α= 1 2 𝑅 𝑅 = 1 2 ,α=30° 以上两式联立,解得 sin β= √3 2 ,β=60° 由几何关系可知∠FOE=α=30°,∠OFE=β-α=30°,故 lEF=R D 点到 E 点的时间 t1= √3 2 𝑅 𝑐 √3 = 3𝑅 2𝑐 E 点到 F 点的时间 t2= 𝑅 𝑐 细光束从开始进入透明体到折射到 OA 轴线上的时间 t=t1+t2= 5𝑅 2𝑐