
第四章过关检测 (时间:90分钟满分:100分) 一、选择题(共10小题,每小题4分,共40分,在每小题给出的四个选项中,第1~7小题只有一 个选项符合题目要求,第8~10小题有多个选项符合题目要求,全部选对的得4分,选对但不全 的得2分,有选错或不答的得0分) 1下列说法正确的是() A.全息照相利用了激光的衍射成像 B.激光测距是利用激光的平行度好 C.用激光“焊接”剥落的视网膜利用了激光的相干性好 D.激光刻录利用激光的亮度高 答案B 解析全息照相利用了激光相千性好的特性,故选项A错误;激光测距是利用激光的平行度好, 故选项B正确:用激光“焊接”剥落的视网膜利用了激光的能量较高、沿直线传播的特点,故选 项C错误:激光刻录利用激光的平行度好,故选项D错误。 2.关于下列现象所涉及的光学知识,下列说法正确的是 () 玻璃坦克外部 川 坦克内部 乙 A.图甲检查工件的平整度是利用光的衍射现象 B.医用内窥镜是利用光的干涉现象 C.图乙在坦克内壁上开孔安装玻璃是利用光的折射现象扩大视野 D.泊松亮斑是由光的偏振现象产生的 答案C 解析题图甲检查工件的平整度是利用光的干涉现象,故选项A错误;医用内窥镜是利用光的 全反射现象,故选项B错误;题图乙在坦克内壁上开孔安装玻璃是利用光的折射现象扩大视 野,故选项C正确;泊松亮斑是由光的衍射现象产生的,故选项D错误。 3.下图为单反照相机取景器的示意图,ABCDE为五棱镜的一个截面,AB⊥BC,光线垂直AB射 入,分别在CD和EA上发生反射,且两次反射的入射角相等,最后光线垂直BC射出,若两次反 射都为全反射,则该五棱镜的折射率( D 五棱镜 C至人眼 B A.最小值为VZ B.最大值为VZ C.最小值为n25° D.最大值为in225 1 答案c 解析设入射到CD面上的入射角为O,因为在CD和EA上发生反射,且两次反射的入射角相 等,根据几何关系有40=90°解得0=25”,根据sim0片解得最小折射丰n22,故选项 C正确
第四章过关检测 (时间:90 分钟 满分:100 分) 一、选择题(共 10 小题,每小题 4 分,共 40 分,在每小题给出的四个选项中,第 1~7 小题只有一 个选项符合题目要求,第 8~10 小题有多个选项符合题目要求,全部选对的得 4 分,选对但不全 的得 2 分,有选错或不答的得 0 分) 1.下列说法正确的是( ) A.全息照相利用了激光的衍射成像 B.激光测距是利用激光的平行度好 C.用激光“焊接”剥落的视网膜利用了激光的相干性好 D.激光刻录利用激光的亮度高 答案 B 解析全息照相利用了激光相干性好的特性,故选项 A 错误;激光测距是利用激光的平行度好, 故选项 B 正确;用激光“焊接”剥落的视网膜利用了激光的能量较高、沿直线传播的特点,故选 项 C 错误;激光刻录利用激光的平行度好,故选项 D 错误。 2.关于下列现象所涉及的光学知识,下列说法正确的是 ( ) A.图甲检查工件的平整度是利用光的衍射现象 B.医用内窥镜是利用光的干涉现象 C.图乙在坦克内壁上开孔安装玻璃是利用光的折射现象扩大视野 D.泊松亮斑是由光的偏振现象产生的 答案 C 解析题图甲检查工件的平整度是利用光的干涉现象,故选项 A 错误;医用内窥镜是利用光的 全反射现象,故选项 B 错误;题图乙在坦克内壁上开孔安装玻璃是利用光的折射现象扩大视 野,故选项 C 正确;泊松亮斑是由光的衍射现象产生的,故选项 D 错误。 3.下图为单反照相机取景器的示意图,ABCDE 为五棱镜的一个截面,AB⊥BC,光线垂直 AB 射 入,分别在 CD 和 EA 上发生反射,且两次反射的入射角相等,最后光线垂直 BC 射出,若两次反 射都为全反射,则该五棱镜的折射率( ) A.最小值为√2 B.最大值为√2 C.最小值为 1 sin22.5° D.最大值为 1 sin22.5° 答案 C 解析设入射到 CD 面上的入射角为 θ,因为在 CD 和 EA 上发生反射,且两次反射的入射角相 等,根据几何关系有 4θ=90°,解得 θ=22.5°,根据 sin θ= 1 𝑛 ,解得最小折射率 n= 1 sin22.5° ,故选项 C 正确
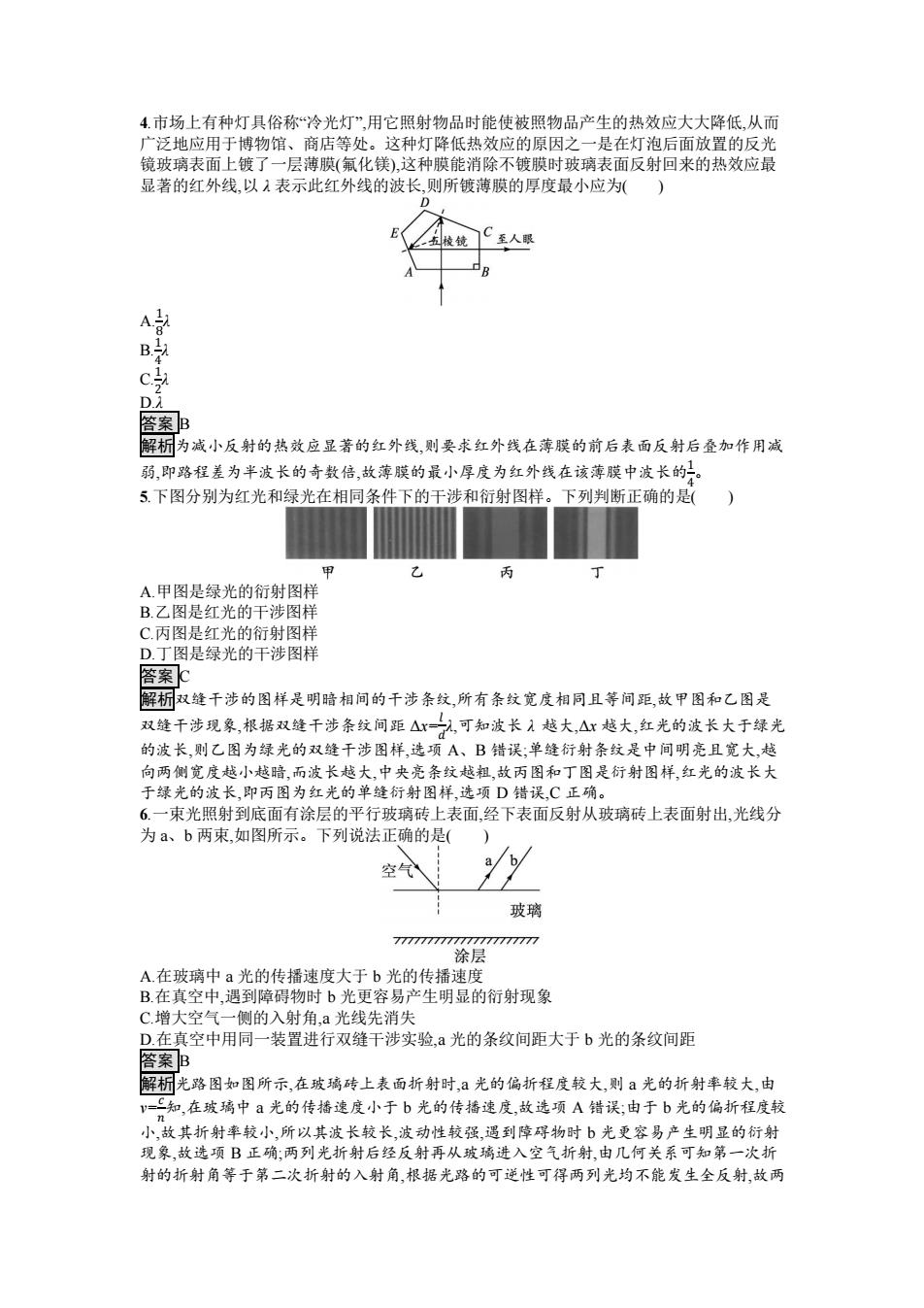
4.市场上有种灯具俗称“冷光灯”,用它照射物品时能使被照物品产生的热效应大大降低,从而 广泛地应用于博物馆、商店等处。这种灯降低热效应的原因之一是在灯泡后面放置的反光 镜玻璃表面上镀了一层薄膜(氟化镁),这种膜能消除不镀膜时玻璃表面反射回来的热效应最 显著的红外线,以1表示此红外线的波长,则所镀薄膜的厚度最小应为() ”至人眼 B D 答案B 解析为减小反射的热效应显著的红外线,则要求红外线在薄膜的前后表面反射后叠加作用减 弱,即路程差为半波长的奇数倍,故薄膜的最小厚度为红外线在该薄膜中波长的。 5.下图分别为红光和绿光在相同条件下的干涉和衍射图样。下列判断正确的是() 甲 乙 丙 A.甲图是绿光的衍射图样 B.乙图是红光的干涉图样 C.丙图是红光的衍射图样 D.丁图是绿光的干涉图样 答案c 解桐权缝干涉的图样是明暗相间的干涉条纹,所有条纹宽度相同且等间距,故甲图和乙图是 双缝千涉现象,根据双缝千涉条纹间距△x=二入,可知波长入越大,△x越大,红光的波长大于绿光 的波长,则乙图为绿光的双缝千涉图样,选项A、B错误;单缝衍射条纹是中间明亮且宽大,越 向两侧宽度越小越暗,而波长越大,中央亮条纹越粗,故丙图和丁图是衍射图样,红光的波长大 于绿光的波长,即丙图为红光的单缝衍射图样,选项D错误,C正确。 6.一束光照射到底面有涂层的平行玻璃砖上表面,经下表面反射从玻璃砖上表面射出,光线分 为a、b两束,如图所示。下列说法正确的是( 空气 玻璃 7777777777777777777777 涂层 A.在玻璃中a光的传播速度大于b光的传播速度 B.在真空中,遇到障碍物时b光更容易产生明显的衍射现象 C.增大空气一侧的入射角,a光线先消失 D.在真空中用同一装置进行双缝干涉实验,ā光的条纹间距大于b光的条纹间距 答案B 解析光路图如图所示,在玻璃砖上表面折射时,a光的偏折程度较大,则a光的折射率较大,由 知,在玻璃中a光的传播速度小于b光的传播速度,故选项A错误:由于b光的偏折程度较 小,故其折射率较小,所以其波长较长,波动性较强,遇到障碍物时b光更容易产生明显的衍射 现象,故选项B正确;两列光折射后经反射再从玻璃进入空气折射,由几何关系可知第一次折 射的折射角等于第二次折射的入射角,根据光路的可逆性可得两列光均不能发生全反射,故两
4.市场上有种灯具俗称“冷光灯”,用它照射物品时能使被照物品产生的热效应大大降低,从而 广泛地应用于博物馆、商店等处。这种灯降低热效应的原因之一是在灯泡后面放置的反光 镜玻璃表面上镀了一层薄膜(氟化镁),这种膜能消除不镀膜时玻璃表面反射回来的热效应最 显著的红外线,以 λ 表示此红外线的波长,则所镀薄膜的厚度最小应为( ) A. 1 8 λ B. 1 4 λ C. 1 2 λ D.λ 答案 B 解析为减小反射的热效应显著的红外线,则要求红外线在薄膜的前后表面反射后叠加作用减 弱,即路程差为半波长的奇数倍,故薄膜的最小厚度为红外线在该薄膜中波长的1 4。 5.下图分别为红光和绿光在相同条件下的干涉和衍射图样。下列判断正确的是( ) A.甲图是绿光的衍射图样 B.乙图是红光的干涉图样 C.丙图是红光的衍射图样 D.丁图是绿光的干涉图样 答案 C 解析双缝干涉的图样是明暗相间的干涉条纹,所有条纹宽度相同且等间距,故甲图和乙图是 双缝干涉现象,根据双缝干涉条纹间距 Δx= 𝑙 𝑑 λ,可知波长 λ 越大,Δx 越大,红光的波长大于绿光 的波长,则乙图为绿光的双缝干涉图样,选项 A、B 错误;单缝衍射条纹是中间明亮且宽大,越 向两侧宽度越小越暗,而波长越大,中央亮条纹越粗,故丙图和丁图是衍射图样,红光的波长大 于绿光的波长,即丙图为红光的单缝衍射图样,选项 D 错误,C 正确。 6.一束光照射到底面有涂层的平行玻璃砖上表面,经下表面反射从玻璃砖上表面射出,光线分 为 a、b 两束,如图所示。下列说法正确的是( ) A.在玻璃中 a 光的传播速度大于 b 光的传播速度 B.在真空中,遇到障碍物时 b 光更容易产生明显的衍射现象 C.增大空气一侧的入射角,a 光线先消失 D.在真空中用同一装置进行双缝干涉实验,a 光的条纹间距大于 b 光的条纹间距 答案 B 解析光路图如图所示,在玻璃砖上表面折射时,a 光的偏折程度较大,则 a 光的折射率较大,由 v= 𝑐 𝑛 知,在玻璃中 a 光的传播速度小于 b 光的传播速度,故选项 A 错误;由于 b 光的偏折程度较 小,故其折射率较小,所以其波长较长,波动性较强,遇到障碍物时 b 光更容易产生明显的衍射 现象,故选项 B 正确;两列光折射后经反射再从玻璃进入空气折射,由几何关系可知第一次折 射的折射角等于第二次折射的入射角,根据光路的可逆性可得两列光均不能发生全反射,故两

列光不会消失,故选项C错误;a光的折射率大,频率大,则波长小,根据△r,a光的条纹间距 小于b光的条纹间距,故选项D错误。 玻璃 7777777977777777 涂层 7.在透明的均匀介质内有一球状空气泡,O为球心,一束包含、b两种单色光的细光束从介 质射入气泡,A为入射点,之后a、b光分别从C、D两点射向介质,细光束在A点的入射角为 30°,介质对a光的折射率n=√2,下列说法正确的是( 307 A.在该介质中,a光的传播速度比b光的传播速度大 B.a光射出空气泡后的传播方向相对于射入空气泡前的传播方向偏转角为30° C.当a光通过单缝时,若缝的宽度小于a光波长,a光不能发生衍射现象 D.若由a光和b光组成的一束细光束从空气斜射向水中,在不断增大入射角时,a的折射光会 先消失 答案B 解析根据光在A点的折射可知,a光的偏折角大于b光的偏折角,所以a光的折射率大于b光 的折射率,由v得知,在该介质中,a光的传播速度比b光的传播速度小,选项A错误;设a光 在A点的入射角为i,折射角为n,由折射定律得n二,得sn⅓=sn1V2sn30°票,得 sini ra=45°,根据光路可逆性和几何知识可知,a光线从C点射出时,入射角和折射角分别等于A 点折射时折射角和入射角,则偏向角为0=2(ra-)=30°,选项B正确:对照衍射的条件知,当a 光通过单缝时,若缝的宽度小于a光波长,a光能发生明显衍射现象,选项C错误;发生全反射 的条件是光从光密介质射向光疏介质,光束从空气斜射向水中,不能发生全反射,折射光线不 会消失,选项D错误。 8.把一个曲率半径很大的凸透镜的弯曲表面压在另一个玻璃平面上,让单色光从上方射入(如 图甲),这时可以看到亮暗相间的同心圆(如图乙),这个现象是牛顿首先发现的,这些同心圆叫 作牛顿环,为了使同一级圆环的半径变大(例如中心数起的第二道圆环),则应() 入射光 A将凸透镜的曲率半径变大 B.将凸透镜的曲率半径变小 C.改用波长更长的单色光照射 D.改用波长更短的单色光照射 答案AC 解析当光程差为波长的整数倍时是亮条纹,当光程差为半个波长的奇数倍时是暗条纹。将凸 透镜的曲率半径变大,与透镜中心等距离位置的空气层厚度变小,出现同一亮条纹的厚度由中 心向外偏移,同一级圆环的半径变大;相反,凸透镜的曲率半径变小,同一级圆环的半径变小,故 选项A正确,B错误;改用波长更长的单色光照射,出现同一级亮纹的光程差变大,空气层厚度
列光不会消失,故选项 C 错误;a 光的折射率大,频率大,则波长小,根据 Δx= 𝑙 𝑑 λ,a 光的条纹间距 小于 b 光的条纹间距,故选项 D 错误。 7.在透明的均匀介质内有一球状空气泡,O 为球心,一束包含 a、b 两种单色光的细光束从介 质射入气泡,A 为入射点,之后 a、b 光分别从 C、D 两点射向介质,细光束在 A 点的入射角为 30°,介质对 a 光的折射率 n=√2,下列说法正确的是( ) A.在该介质中,a 光的传播速度比 b 光的传播速度大 B.a 光射出空气泡后的传播方向相对于射入空气泡前的传播方向偏转角为 30° C.当 a 光通过单缝时,若缝的宽度小于 a 光波长,a 光不能发生衍射现象 D.若由 a 光和 b 光组成的一束细光束从空气斜射向水中,在不断增大入射角时,a 的折射光会 先消失 答案 B 解析根据光在 A 点的折射可知,a 光的偏折角大于 b 光的偏折角,所以 a 光的折射率大于 b 光 的折射率,由 v= 𝑐 𝑛 得知,在该介质中,a 光的传播速度比 b 光的传播速度小,选项 A 错误;设 a 光 在 A 点的入射角为 i,折射角为 ra ,由折射定律得 n= sin 𝑟a sin𝑖 ,得 sin ra=nsin i=√2sin 30°= √2 2 ,得 ra=45°,根据光路可逆性和几何知识可知,a 光线从 C 点射出时,入射角和折射角分别等于 A 点折射时折射角和入射角,则偏向角为 θ=2(ra-i)=30°,选项 B 正确;对照衍射的条件知,当 a 光通过单缝时,若缝的宽度小于 a 光波长,a 光能发生明显衍射现象,选项 C 错误;发生全反射 的条件是光从光密介质射向光疏介质,光束从空气斜射向水中,不能发生全反射,折射光线不 会消失,选项 D 错误。 8.把一个曲率半径很大的凸透镜的弯曲表面压在另一个玻璃平面上,让单色光从上方射入(如 图甲),这时可以看到亮暗相间的同心圆(如图乙),这个现象是牛顿首先发现的,这些同心圆叫 作牛顿环,为了使同一级圆环的半径变大(例如中心数起的第二道圆环),则应( ) A.将凸透镜的曲率半径变大 B.将凸透镜的曲率半径变小 C.改用波长更长的单色光照射 D.改用波长更短的单色光照射 答案 AC 解析当光程差为波长的整数倍时是亮条纹,当光程差为半个波长的奇数倍时是暗条纹。将凸 透镜的曲率半径变大,与透镜中心等距离位置的空气层厚度变小,出现同一亮条纹的厚度由中 心向外偏移,同一级圆环的半径变大;相反,凸透镜的曲率半径变小,同一级圆环的半径变小,故 选项 A 正确,B 错误;改用波长更长的单色光照射,出现同一级亮纹的光程差变大,空气层厚度
应变大,所以要使同一级圆环的半径变大,可以改用波长更长的单色光照射,故选项C正确,D 错误。 9.如图所示,水下光源S向水面A点发射一束光线,折射光线分别为a、b两束,则() b A.a、b两束光相比较,在真空中a光的波长较长 B.在水中a光的速度与b光的一样大 C.若保持入射点A位置不变,将入射光线顺时针旋转,从水面上方观察,b光先消失 D.用同一双缝干涉实验装置分别用a、b光做实验,a光干涉条纹间距大于b光干涉条纹间距 答案ACD 解析由题图可知,两光束的入射角i相同,折射角有r<,根据折射定律可知折射率na<,水 对b光的折射率较大,b光的频率更大,则在真空中a光的波长较长,b光的波长较短,故选项A 正确;由公式v-分析得知,在水中a光的速度比b光的速度大,故选项B错误,a光的折射率 小,根据临界角公式sinC可知,a光的临界角较大,b先发生全反射,从水面上方观察,b光先 消失,故选项C正确:用同一双缝千涉实验装置分别以a、b光做实验,a光的波长较长,b光的 波长短,a光千涉条纹间距大于b光干涉条纹间距,故选项D正确。 10.共享单车的尾灯反光标志的截面如图甲所示,它是一块锯齿形的透明材料,锯齿形状为等 腰直角三角形,直角边长为α,折射率为1。某同学取来做光学演示,如图乙所示,将尾灯平放 在折射率为m(1<m)的液体上方,用平行光束向下竖直照射,有关光学现象的表述及其解释 正确的是() 甲 A尾灯在液面以上时,上表面比较明亮,光在尾灯上表面发生镜面反射 B.尾灯在液面以上时,上表面比较明亮,光在尾灯下表面发生全反射,透明材料折射率1≥√2 C尾灯锯齿状部分入液深度为h时(h<2),有明暗条纹,明纹总宽度为x=42a-8勋 D.尾灯锯齿状部分全部在液面以下时,上表面比较暗,尾灯上表面无反射光 答案BC 解桐尾灯在液面以上时,光线垂直射到上表面后沿直线射到下表面的直角边上,然后通过镜 面反射到另一直角边上,再通过另一直角边的反射竖直向上射出上表面,则可看到下表面比较 明亮,光在尾灯下表面发生全反射,此时满足C≤45°,即1≥√Z,选项A错误,B正确:如图所 示,光线射到直角边上时,在液体上部分的光线仍然发生全反射,通过另一直角边射回到空气 中,我们看到的此部分是明纹,而射到液面以下部分的光线,由于1<可知部分光线会发生折 射而射入液体中,我们看到的是暗条纹,则由几何关系可知,四个等腰三角形中看到的亮纹总 宽度是4×2(acos45°-h)=4√Za-8h,选项C正确;尾灯锯齿状部分全部在液面以下时,尾灯上 表面仍有反射光,但是上表面比较暗,选项D错误。 二、实验题(共3小题,共18分)
应变大,所以要使同一级圆环的半径变大,可以改用波长更长的单色光照射,故选项 C 正确,D 错误。 9.如图所示,水下光源 S 向水面 A 点发射一束光线,折射光线分别为 a、b 两束,则( ) A.a、b 两束光相比较,在真空中 a 光的波长较长 B.在水中 a 光的速度与 b 光的一样大 C.若保持入射点 A 位置不变,将入射光线顺时针旋转,从水面上方观察,b 光先消失 D.用同一双缝干涉实验装置分别用 a、b 光做实验,a 光干涉条纹间距大于 b 光干涉条纹间距 答案 ACD 解析由题图可知,两光束的入射角 i 相同,折射角有 ra<rb,根据折射定律可知折射率 na<nb,水 对 b 光的折射率较大,b 光的频率更大,则在真空中 a 光的波长较长,b 光的波长较短,故选项 A 正确;由公式 v= 𝑐 𝑛分析得知,在水中 a 光的速度比 b 光的速度大,故选项 B 错误;a 光的折射率 小,根据临界角公式 sin C=1 𝑛可知,a 光的临界角较大,b 先发生全反射,从水面上方观察,b 光先 消失,故选项 C 正确;用同一双缝干涉实验装置分别以 a、b 光做实验,a 光的波长较长,b 光的 波长短,a 光干涉条纹间距大于 b 光干涉条纹间距,故选项 D 正确。 10.共享单车的尾灯反光标志的截面如图甲所示,它是一块锯齿形的透明材料,锯齿形状为等 腰直角三角形,直角边长为 a,折射率为 n1。某同学取来做光学演示,如图乙所示,将尾灯平放 在折射率为 n2(n1<n2)的液体上方,用平行光束向下竖直照射,有关光学现象的表述及其解释 正确的是( ) A.尾灯在液面以上时,上表面比较明亮,光在尾灯上表面发生镜面反射 B.尾灯在液面以上时,上表面比较明亮,光在尾灯下表面发生全反射,透明材料折射率 n1≥√2 C.尾灯锯齿状部分入液深度为 h 时(ℎ < √2𝑎 2 ),有明暗条纹,明纹总宽度为 x=4√2a-8h D.尾灯锯齿状部分全部在液面以下时,上表面比较暗,尾灯上表面无反射光 答案 BC 解析尾灯在液面以上时,光线垂直射到上表面后沿直线射到下表面的直角边上,然后通过镜 面反射到另一直角边上,再通过另一直角边的反射竖直向上射出上表面,则可看到下表面比较 明亮,光在尾灯下表面发生全反射,此时满足 C≤45°,即 n1≥√2,选项 A 错误,B 正确;如图所 示,光线射到直角边上时,在液体上部分的光线仍然发生全反射,通过另一直角边射回到空气 中,我们看到的此部分是明纹,而射到液面以下部分的光线,由于 n1<n2 可知部分光线会发生折 射而射入液体中,我们看到的是暗条纹,则由几何关系可知,四个等腰三角形中看到的亮纹总 宽度是 4×2(acos 45°-h)=4√2a-8h,选项 C 正确;尾灯锯齿状部分全部在液面以下时,尾灯上 表面仍有反射光,但是上表面比较暗,选项 D 错误。 二、实验题(共 3 小题,共 18 分)

11.(4分)如图所示,在杨氏双缝干涉实验中,选用激光的频率为6.0×1014Hz,测得屏上P点距 双缝S1和S2的路程差为1.25×106m,则在这里出现的应是 (选填“明条纹”或“暗 条纹”)。现改用频率为8.0×1014Hz的激光进行上述实验,保持其他条件不变,则屏上的条纹 间距将 (选填变宽变窄”或“不变”),已知光速c=3×10m/s。 激光 挡板 屏 答案暗条纹变窄 解标已知屏上P点距双缝S1和的路程差,结合c=可知n125x10m=125x10m-5,5 9 为奇数,即光程差为半波长的奇数倍,所以P点为暗条纹。激光频率变大,波长变小,根据 △=可知屏上的条纹间距将变窄。 12.(6分)在用插针法测定玻璃的折射率的实验中,甲、乙两位同学分别使用矩形玻璃砖和梯 形玻璃砖进行实验。 Q 丙 (1)甲同学在纸上画出的界面a'、bb与矩形玻璃砖位置的关系如图甲所示,若其他操作均正 确,且以aa'、bb'为界面画光路图,则测得的折射率与真实值相比 (选填“偏大*偏小*“不变”或“可能偏小、偏大或不变”)。 (2)乙同学使用梯形玻璃砖经正确操作插好了4枚大头针,如图乙所示,其垂直投影平面图如 图丙所示。该玻璃砖的折射率n= 。(结果保留3位有效数字) (3)为了观测光在玻璃砖不同表面的折射现象,乙同学用梯形玻璃砖又做了两次实验,经正确 操作共插好了8枚大头针,如图丁所示,图中P1和P2是同一入射光线上的2枚大头针,其对应 出射光线上的2枚大头针是P3和 (选填“A”或“B”)。 答案1)可能偏小、偏大或不变 (2)1.51(1.48-1.54都算对) (3)A 解析1)甲同学的测量可能出现三种可能,光路图如图所示,当出射点为c时,测量值与真实值 相同;当出射点在c左侧时,测量值小于真实值:当出射点在c右侧时,测量值大于真实值。故 丙同学测得的折射率与真实值相比可能偏大、偏小或不变。 (2)作图如下,假设每小格边长为1,由n加得 siny 5.4 5.42+42 2.2 =151。 2.22+3.62
11.(4 分)如图所示,在杨氏双缝干涉实验中,选用激光的频率为 6.0×1014 Hz,测得屏上 P 点距 双缝 S1 和 S2 的路程差为 1.25×10-6 m,则在这里出现的应是 (选填“明条纹”或“暗 条纹”)。现改用频率为 8.0×1014 Hz 的激光进行上述实验,保持其他条件不变,则屏上的条纹 间距将 (选填“变宽”“变窄”或“不变”),已知光速 c=3×108 m/s。 答案暗条纹 变窄 解析已知屏上 P 点距双缝 S1 和 S2 的路程差,结合 c=λf 可知 n= 1.25×10 -6 m 𝜆 2 = 1.25×10 -6 m 𝑐 2𝑓 =5,5 为奇数,即光程差为半波长的奇数倍,所以 P 点为暗条纹。激光频率变大,波长变小,根据 Δx= 𝑙 𝑑 λ 可知屏上的条纹间距将变窄。 12.(6 分)在用插针法测定玻璃的折射率的实验中,甲、乙两位同学分别使用矩形玻璃砖和梯 形玻璃砖进行实验。 (1)甲同学在纸上画出的界面 aa'、bb'与矩形玻璃砖位置的关系如图甲所示,若其他操作均正 确,且以 aa'、bb'为界面画光路图,则测得的折射率与真实值相比 (选填“偏大”“偏小”“不变”或“可能偏小、偏大或不变”)。 (2)乙同学使用梯形玻璃砖经正确操作插好了 4 枚大头针,如图乙所示,其垂直投影平面图如 图丙所示。该玻璃砖的折射率 n= 。(结果保留 3 位有效数字) (3)为了观测光在玻璃砖不同表面的折射现象,乙同学用梯形玻璃砖又做了两次实验,经正确 操作共插好了 8 枚大头针,如图丁所示,图中 P1 和 P2 是同一入射光线上的 2 枚大头针,其对应 出射光线上的 2 枚大头针是 P3 和 (选填“A”或“B”)。 答案(1)可能偏小、偏大或不变 (2)1.51(1.48~1.54 都算对) (3)A 解析(1)甲同学的测量可能出现三种可能,光路图如图所示,当出射点为 c 时,测量值与真实值 相同;当出射点在 c 左侧时,测量值小于真实值;当出射点在 c 右侧时,测量值大于真实值。故 丙同学测得的折射率与真实值相比可能偏大、偏小或不变。 (2)作图如下,假设每小格边长为 1,由 n= sin𝛼 sin𝛾 得 n= 5.4 √ 5.4 2+4 2 2.2 √ 2.2 2+3.6 2 =1.51

(3)由PP射入后,第一次折射时入射角大于折射角,第二次折射时折射角大于入射角,经过A 点。 13.(8分)我们用以下装置来做用双缝干涉测量光的波长的实验。 (1)光具座上放置的光学元件如下图所示,M为 光源凸透镜M单缝双缝遮光筒 像屏 H 测量头 (2)在本实验中,测量△x是本实验的关键,观察图像,在实际操作中△x的测量应选下图中的 (选填“甲”或“乙图。 △i 甲 3△x (3)已知实验所用的测量头由分划板、滑块、目镜、手轮等构成,使用50分度的游标卡尺。 某同学在成功观察到干涉图像后,开始进行数据记录。从目镜中观察干涉图像,同时调节手 轮,总共测量了5条亮纹之间的距离,初末位置游标卡尺的示数如图丙和丁所示,则相邻两条 亮纹的间距△r= mm。 52 0 2 3 4 cm a 010203040 丙 52 0 2 3 4 5cm u4laT 010203040 入 (4)为了增加光屏上相邻两条纹之间的距离,可以_。 A.增大单缝与双缝之间的距离 B.增大双缝与毛玻璃之间的距离
(3)由 P1P2 射入后,第一次折射时入射角大于折射角,第二次折射时折射角大于入射角,经过 A 点。 13.(8 分)我们用以下装置来做用双缝干涉测量光的波长的实验。 (1)光具座上放置的光学元件如下图所示,M 为 。 (2)在本实验中,测量 Δx 是本实验的关键,观察图像,在实际操作中 Δx 的测量应选下图中的 (选填“甲”或“乙”)图。 甲 乙 (3)已知实验所用的测量头由分划板、滑块、目镜、手轮等构成,使用 50 分度的游标卡尺。 某同学在成功观察到干涉图像后,开始进行数据记录。从目镜中观察干涉图像,同时调节手 轮,总共测量了 5 条亮纹之间的距离,初末位置游标卡尺的示数如图丙和丁所示,则相邻两条 亮纹的间距 Δx= mm。 丙 丁 (4)为了增加光屏上相邻两条纹之间的距离,可以 。 A.增大单缝与双缝之间的距离 B.增大双缝与毛玻璃之间的距离

C将红色滤光片改为绿色滤光片 D.增大双缝之间的距离 答案1)滤光片 (2)乙 (3)1.99 (4)B 解析2)在实际操作中标度线在明条纹中容易观察,且先测量3△x的长度再除以3,得出的△x 误差更小,故选乙图。 (3)初末位置游标卡尺的示数分别为5mm+0.02mm×23=5.46mm,13mm+0.02mm×20=13.40 mm,则条纹间距△x=1340mm-546mm=1.99mm. (4)根据△-之可知,增大单缝与双缝之间的距离,对条纹间距无影响,选项A错误;增大双缝与 毛玻璃之间的距离,即增大1,可增大条纹间距,选项B正确:将红色滤光片改为绿色滤光片,则 波长入变小,则条纹间距变小,选项C错误;增大双缝之间的距离,则d变大,则条纹间距减小, 选项D错误。 三、计算题(共4小题,共42分。解答应写出必要的文字说明、方程式和重要演算步骤,只写 出最后答案不能得分,有数值计算的题,答案中必须明确写出数值和单位) 14.(9分)下图为双缝干涉测量光的波长的实验示意图,双缝S1和S2间距为0.80mm,双缝到屏 的距离为0.80m,波长为500nm的单色平行光垂直入射到双缝S,和S2上,在屏上形成干涉条 纹,中心轴线OO'上方第一条亮纹中心位置在P处,第三条亮纹中心位置在P2处,现有1号、 2号虫子分别从S和2同时出发,以相同速度沿垂直屏的方向飞行,1号虫子到达屏后,沿屏 直线爬行到P1,2号虫子到达屏后,沿屏直线爬行到P,假定两只虫子爬行速度均为103m/s, 则两只虫子运动的时间差为多少? S2 0 答案0.2s 解杨相邻亮条纹的间距为△r之-0.5mm OP1的间距为x=0.5mm OP2的间距为x'=3x=1.5mm 1号虫子爬行的时间为1 x+号 2号虫子爬行的时间为=。 两只虫子飞行的时间相同,因此两只虫子运动的时间差为△=-1延0.2s。 15.(9分)如图所示,直角三角形ABC为一棱镜的横截面,∠A=90°,∠B=30°。一束光线平行 于底边BC射到AB边上并进入棱镜,然后垂直于AC边射出。 (1)求棱镜的折射率。 (2)保持AB边上的入射点不变,逐渐减小入射角,直到BC边上恰好有光线射出。求此时AB 边上入射角的正弦。 答1)W3 (2③2 2
C.将红色滤光片改为绿色滤光片 D.增大双缝之间的距离 答案(1)滤光片 (2)乙 (3)1.99 (4)B 解析(2)在实际操作中标度线在明条纹中容易观察,且先测量 3Δx 的长度再除以 3,得出的 Δx 误差更小,故选乙图。 (3)初末位置游标卡尺的示数分别为 5 mm+0.02 mm×23=5.46 mm,13 mm+0.02 mm×20=13.40 mm,则条纹间距 Δx= 13.40mm-5.46 mm 4 =1.99 mm。 (4)根据 Δx= 𝑙 𝑑 λ 可知,增大单缝与双缝之间的距离,对条纹间距无影响,选项 A 错误;增大双缝与 毛玻璃之间的距离,即增大 l,可增大条纹间距,选项 B 正确;将红色滤光片改为绿色滤光片,则 波长 λ 变小,则条纹间距变小,选项 C 错误;增大双缝之间的距离,则 d 变大,则条纹间距减小, 选项 D 错误。 三、计算题(共 4 小题,共 42 分。解答应写出必要的文字说明、方程式和重要演算步骤,只写 出最后答案不能得分,有数值计算的题,答案中必须明确写出数值和单位) 14.(9 分)下图为双缝干涉测量光的波长的实验示意图,双缝 S1 和 S2 间距为 0.80 mm,双缝到屏 的距离为 0.80 m,波长为 500 nm 的单色平行光垂直入射到双缝 S1 和 S2 上,在屏上形成干涉条 纹,中心轴线 OO'上方第一条亮纹中心位置在 P1 处,第三条亮纹中心位置在 P2 处,现有 1 号、 2 号虫子分别从 S1 和 S2 同时出发,以相同速度沿垂直屏的方向飞行,1 号虫子到达屏后,沿屏 直线爬行到 P1,2 号虫子到达屏后,沿屏直线爬行到 P2,假定两只虫子爬行速度均为 10-3 m/s, 则两只虫子运动的时间差为多少? 答案 0.2 s 解析相邻亮条纹的间距为 Δx= 𝑙 𝑑 λ=0.5 mm O'P1 的间距为 x=0.5 mm O'P2 的间距为 x'=3x=1.5 mm 1 号虫子爬行的时间为 t1= 𝑥+ 𝑑 2 𝑣 2 号虫子爬行的时间为 t2= 𝑥'- 𝑑 2 𝑣 两只虫子飞行的时间相同,因此两只虫子运动的时间差为 Δt=t2-t1= 𝑥'-𝑥-𝑑 𝑣 =0.2 s。 15.(9 分)如图所示,直角三角形 ABC 为一棱镜的横截面,∠A=90°,∠B=30°。一束光线平行 于底边 BC 射到 AB 边上并进入棱镜,然后垂直于 AC 边射出。 (1)求棱镜的折射率。 (2)保持 AB 边上的入射点不变,逐渐减小入射角,直到 BC 边上恰好有光线射出。求此时 AB 边上入射角的正弦。 答案(1)√3 (2)√3-√2 2

解杨)光路图及相关量如图所示。光束在AB边上折射,由折射定律得二儿式中n是棱镜 的折射率。由几何关系可知a+B=60°,由几何关系和反射定律得B=B'=∠B,则n=V3。 (2)设改变后的入射角为,折射角为?,由折射定律得-儿,依题意,光束在BC边上的入射角 为全反射的临界角0,且sn品由几何关系得0=a+30°,则snV一三。 A B 16.(12分)下图为某种透明介质的截面图,△AOC为等腰直角三角形,BC为半径R=10cm的 四分之一圆弧,AB与水平面屏幕MN垂直并接触于A点。由红光和紫光两种单色光组成的 复色光射向圆心O,在AB分界面上的入射角i=45°,结果在水平屏幕MN上出现两个亮斑。 己知该介质对红光和紫光的折射率分别为m ,2=V2。 A (I)判断在AM和AN两处产生亮斑的颜色。 (2)求两个亮斑间的距离。 答1)在AM处产生的亮斑颜色为红色,在AW处产生的亮斑颜色为红色与紫色的混合色 (2)(5v2+10)cm 图韧1)设红光和紫光的临界角分别为C、G,sinC日=复C-60°,同理 ni C2=45°,i=45°=C2,i=45°<C,所以紫光在AB面发生全反射,而红光在AB面一部分折射, 一部分反射,且由几何关系可知,反射光线与AC垂直,所以在AM处产生的亮斑为红色,在AW 处产生的亮斑为红色与紫色的混合色。 (2)画出光路图如图所示,设折射角为r两个光斑分别为P、P。根据折射定律川疆 求得m晋 由几何知识可得tan4p R 解得laP1=5VZcm 由几何知识可得△OAP2为等腰直角三角形, 解得laP2=l0cm 所以lp1P2=(5V2+10)cm。 17.(12分)如图所示,在注满水的游泳池的池底有一点光源A,它到池边的水平距离为3.0m。 从点光源A射向池边的光线AB与竖直方向的夹角恰好等于全反射的临界角,水的折射率为
解析(1)光路图及相关量如图所示。光束在 AB 边上折射,由折射定律得sin𝑖 sin𝛼 =n,式中 n 是棱镜 的折射率。由几何关系可知 α+β=60°,由几何关系和反射定律得 β=β'=∠B,则 n=√3。 (2)设改变后的入射角为 i',折射角为 α',由折射定律得sin𝑖' sin𝛼' =n,依题意,光束在 BC 边上的入射角 为全反射的临界角 θc,且 sin θc= 1 𝑛 ,由几何关系得 θc=α'+30°,则 sin i'=√3-√2 2 。 16.(12 分)下图为某种透明介质的截面图,△AOC 为等腰直角三角形,BC 为半径 R=10 cm 的 四分之一圆弧,AB 与水平面屏幕 MN 垂直并接触于 A 点。由红光和紫光两种单色光组成的 复色光射向圆心 O,在 AB 分界面上的入射角 i=45°,结果在水平屏幕 MN 上出现两个亮斑。 已知该介质对红光和紫光的折射率分别为 n1= 2√3 3 ,n2=√2。 (1)判断在 AM 和 AN 两处产生亮斑的颜色。 (2)求两个亮斑间的距离。 答案(1)在 AM 处产生的亮斑颜色为红色,在 AN 处产生的亮斑颜色为红色与紫色的混合色 (2)(5√2+10) cm 解析(1)设红光和紫光的临界角分别为 C1、C2,sin C1= 1 𝑛1 = √3 2 ,C1=60°,同理 C2=45°,i=45°=C2,i=45°<C1,所以紫光在 AB 面发生全反射,而红光在 AB 面一部分折射, 一部分反射,且由几何关系可知,反射光线与 AC 垂直,所以在 AM 处产生的亮斑为红色,在 AN 处产生的亮斑为红色与紫色的混合色。 (2)画出光路图如图所示,设折射角为 r,两个光斑分别为 P1、P2。根据折射定律 n1= sin𝑟 sin𝑖 求得 sin r= √6 3 由几何知识可得 tan r= 𝑅 𝑙𝐴𝑃1 解得 lAP1=5√2 cm 由几何知识可得△OAP2 为等腰直角三角形, 解得 lAP2=10 cm 所以 lP1P2=(5√2+10) cm。 17.(12 分)如图所示,在注满水的游泳池的池底有一点光源 A,它到池边的水平距离为 3.0 m。 从点光源 A 射向池边的光线 AB 与竖直方向的夹角恰好等于全反射的临界角,水的折射率为 4 3

-3.0m+ (1)求池内的水深。(结果保留2位有效数字) (2)一救生员坐在离池边不远处的高凳上,他的眼晴到地面的高度为2.0m。当他看到正前下 方的点光源A时,他的眼睛所接收的光线与竖直方向的夹角恰好为45°。求救生员的眼睛 到池边的水平距离。(结果保留1位有效数字) 答1)2.6m(2)0.7m 解杨1)如图所示,设到达池边光线的入射角为。依题意,水的折射率手光线的折射角 0=90°。由折射定律有 -3.0m→ nsin i=sin 0 ① 由几柯关系有s如门F4 ② 式中,1=3.0m,h是池内水的深度。 联立①②式并代入题给数据得 h=v7m=2.6m。 ③ (2)设此时救生员的眼睛到池边的距离为x。依题意,救生员的视线与竖直方向的夹角为 0=45°。 由折射定律有nsin i'=sin0' ④ 式中,'是光线在水面的入射角。 设池底点光源A到水面入射点的水平距离为0,由几何关系得 sin i'= ⑤ x02+h2 x+/=x0+x ⑥ 式中x'-2.0m 联立③④⑤⑥式得x= m-0.7m
(1)求池内的水深。(结果保留 2 位有效数字) (2)一救生员坐在离池边不远处的高凳上,他的眼睛到地面的高度为 2.0 m。当他看到正前下 方的点光源 A 时,他的眼睛所接收的光线与竖直方向的夹角恰好为 45°。求救生员的眼睛 到池边的水平距离。(结果保留 1 位有效数字) 答案(1)2.6 m (2)0.7 m 解析(1)如图所示,设到达池边光线的入射角为 i。依题意,水的折射率 n= 4 3 ,光线的折射角 θ=90°。由折射定律有 nsin i=sin θ ① 由几何关系有 sin i= 𝑙 √𝑙 2+ℎ 2 ② 式中,l=3.0 m,h 是池内水的深度。 联立①②式并代入题给数据得 h=√7 m=2.6 m。 ③ (2)设此时救生员的眼睛到池边的距离为 x。依题意,救生员的视线与竖直方向的夹角为 θ'=45°。 由折射定律有 nsin i'=sin θ' ④ 式中,i'是光线在水面的入射角。 设池底点光源 A 到水面入射点的水平距离为 x0,由几何关系得 sin i'= 𝑥0 √𝑥0 2+ℎ 2 ⑤ x+l=x0+x' ⑥ 式中 x'=2.0 m 联立③④⑤⑥式得 x=(3√ 7 23 -1) m=0.7 m