
第一章过关检测 (时间:90分钟满分:100分) 一、选择题(共10小题,每小题4分,共40分,在每小题给出的四个选项中,第1~7小题只有一 个选项符合题目要求,第8~10小题有多个选项符合题目要求,全部选对的得4分,选对但不全 的得2分,有选错或不答的得0分) 1蹦床是一项运动员从蹦床反弹中表现杂技技巧的竞技运动,一质量为50kg的运动员从离 蹦床1.8m处自由下落,若从运动员接触蹦床到运动员陷至最低点经历了0.2s(g取10m/s2, 不计空气阻力),则这段时间内,下列说法错误的是() A运动员受到的合力冲量大小为300Ns B.重力的冲量大小为100Ns C.蹦床对运动员的冲量大小为200N·s D.运动员动量变化量大小为300kgm/s 答案C 解析设运动员的质量为m,他刚落到蹦床瞬间的速度为,运动员自由下落的过程,只受重力作 用,故机械能守恒,即m2=mgh,解得v=√2gh=6m/s。选取运动员接触蹦床到运动员陷至最 低点的过程为研究过程,取向上为正方向,设蹦床对运动员的平均作用力为F,则有(下 mg)△1=0-m,合力的冲量为动量的变化量,为I-0-mv=0-50×(-6)N·s=300Ns,选项A、D正 确。重力的冲量为-mg△1=-500×0.2Ns=-100Ns,则选项B正确。蹦床对运动员的冲量为 F△1=0-v+mg△1=400Ns,则选项C错误。 2.A、B两物体发生正碰,碰撞前后物体A、B都在同一直线上运动,其位移一时间图像如图 所示。由图可知,物体A、B的质量之比为( +x/m 20 16 B 0 A.11 B.12 C.13 D.3:1 答案 解析由题图知,碰撞前v%-4m/s,B=0,碰撞后va'-阳'-1m/s,由动量守恒定律可知 mAVA+0=mAVA'+mB,解得mB=3mA,选项C正确。 3.两辆质量相同的小车A和B静止于光滑的水平面上,且A车上站有一人,若这个人从A车 跳到B车上,接着又跳回A车,仍与A车保持相对静止,则此时A车的速度 () A等于零 B.小于B车的速度 C.大于B车的速度D.等于B车的速度 答案B 解析人由A车跳上B车,又由B车跳回A车的整个过程中,人与A、B两车组成的系统水平 方向动量守恒,系统初动量为零,所以末态A车与人的动量之和与B车的动量大小相等、方 向相反,A、B两车质量相等,而人站在A车上,即(m人+mA)vA=mBB,故A车的速度小于B车 的速度,故选项B正确。 4.如果没有空气阻力,天上的云变成雨之后落到地面,在经过一路的加速后,到达地面时的速度 会达到300/s,这样的速度基本相当于子弹速度的一半,是非常可怕的。由于空气阻力的作 用,雨滴经过变加速运动,最终做匀速运动,一般而言,暴雨级别的雨滴落地时的速度为8~9 m/s。某次下暴雨时小明同学打着半径为0.5m的雨伞(假设伞面水平,雨水的平均密度为 0.5kgm3),由于下雨使小明增加撑雨伞的力最小约为() A.0.25N
第一章过关检测 (时间:90 分钟 满分:100 分) 一、选择题(共 10 小题,每小题 4 分,共 40 分,在每小题给出的四个选项中,第 1~7 小题只有一 个选项符合题目要求,第 8~10 小题有多个选项符合题目要求,全部选对的得 4 分,选对但不全 的得 2 分,有选错或不答的得 0 分) 1.蹦床是一项运动员从蹦床反弹中表现杂技技巧的竞技运动,一质量为 50 kg 的运动员从离 蹦床 1.8 m 处自由下落,若从运动员接触蹦床到运动员陷至最低点经历了 0.2 s(g 取 10 m/s2 , 不计空气阻力),则这段时间内,下列说法错误的是( ) A.运动员受到的合力冲量大小为 300 N·s B.重力的冲量大小为 100 N·s C.蹦床对运动员的冲量大小为 200 N·s D.运动员动量变化量大小为 300 kg·m/s 答案 C 解析设运动员的质量为 m,他刚落到蹦床瞬间的速度为 v,运动员自由下落的过程,只受重力作 用,故机械能守恒,即 1 2 mv2=mgh,解得 v=√2𝑔ℎ=6 m/s。选取运动员接触蹦床到运动员陷至最 低点的过程为研究过程,取向上为正方向,设蹦床对运动员的平均作用力为𝐹,则有(𝐹- mg)Δt=0-mv;合力的冲量为动量的变化量,为 I=0-mv=0-50×(-6) N·s=300 N·s,选项 A、D 正 确。重力的冲量为-mgΔt=-500×0.2 N·s=-100 N·s,则选项 B 正确。蹦床对运动员的冲量为 𝐹Δt=0-mv+mgΔt=400 N·s,则选项 C 错误。 2.A、B 两物体发生正碰,碰撞前后物体 A、B 都在同一直线上运动,其位移—时间图像如图 所示。由图可知,物体 A、B 的质量之比为( ) A.1∶1 B.1∶2 C.1∶3 D.3∶1 答案 C 解析由题图知,碰撞前 vA=4 m/s,vB=0,碰撞后 vA'=vB'=1 m/s,由动量守恒定律可知 mAvA+0=mAvA'+mBvB',解得 mB=3mA,选项 C 正确。 3.两辆质量相同的小车 A 和 B 静止于光滑的水平面上,且 A 车上站有一人,若这个人从 A 车 跳到 B 车上,接着又跳回 A 车,仍与 A 车保持相对静止,则此时 A 车的速度 ( ) A.等于零 B.小于 B 车的速度 C.大于 B 车的速度 D.等于 B 车的速度 答案 B 解析人由 A 车跳上 B 车,又由 B 车跳回 A 车的整个过程中,人与 A、B 两车组成的系统水平 方向动量守恒,系统初动量为零,所以末态 A 车与人的动量之和与 B 车的动量大小相等、方 向相反,A、B 两车质量相等,而人站在 A 车上,即(m 人+mA)vA=mBvB,故 A 车的速度小于 B 车 的速度,故选项 B 正确。 4.如果没有空气阻力,天上的云变成雨之后落到地面,在经过一路的加速后,到达地面时的速度 会达到 300 m/s,这样的速度基本相当于子弹速度的一半,是非常可怕的。 由于空气阻力的作 用,雨滴经过变加速运动,最终做匀速运动,一般而言,暴雨级别的雨滴落地时的速度为 8~9 m/s。 某次下暴雨时小明同学打着半径为 0.5 m 的雨伞(假设伞面水平,雨水的平均密度为 0.5 kg/m3 ),由于下雨使小明增加撑雨伞的力最小约为( ) A.0.25 N

B.2.5N C.25N D.250N 答案 解析设时间1内,落到雨伞上雨水的质量为m,根据动量定理有F1=m,m=pvtm2,解得 F=pw2π2,代入数值解得F=25N,选项C正确。 5.一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒打击后反向水平飞回,速 度大小变为45m/s,设球棒与垒球的作用时间为0.01s。下列说法正确的是 () A.垒球的动量变化量大小为3.6kgm/s B.球棒对垒球的冲量大小为126N·s C.球棒对垒球的平均作用力大小为1260N D.球棒对垒球做的功为36J 答案C 解析设垒球的初速度0=25m/s的方向为正方向,则末速度为1=-45m/s,动量的变化量 △p=1-mo=-12.6kgm/s,即垒球的动量变化量大小为12.6kgm/s,故选项A错误;由动量定 理I=△p可知,球棒对垒球的冲量大小为12.6Ns,故选项B错误;由冲量的定义I=F1可知,球 棒对垒球的平均作用力大小为下=2=1260N,故选项C正确;球棒对垒球作用的过程,由动 能定理可知,球棒对垒球做的功为Wmv2-m。2-126J,故选项D错误。 6.如图所示,光滑的四分之一圆弧轨道质量为m,静止在光滑水平面上,一个质量为m的物块 在水平地面上以大小为%的初速度向右运动并无能量损失地滑上圆弧轨道,当物块运动到圆 弧轨道上某一位置时,物块向上的速度为零,此时物块与圆弧轨道的动能之比为1:2,则此时 物块的动能与重力势能之比为(以地面为参考平面)( m 72 力7777777777777777777 A.12 B.13 C.16 D19 答案c 解析因为水平面光滑,轨道和物块组成的系统水平方向动量守恒,当物块向上的速度为零时, 两物体速度相同,又国为此时物块与圆孤轨道的动能之比为12,即2m2:m2-1:2,得到 m,m'=1:2;根据动量守恒定律有mw=(m+m)m,得到%=3v,根据能量守恒定律有mv。2= m+m+Er,解得En吉mp。2,此时物块的动能为E之m2gmo2,所以此时物块的动能与 重力势能之比为1:6,故选项C正确,A、B、D错误。 7.一辆运沙车按着大喇叭轰隆隆地从旁边开过.小明想装沙时运沙车都是停在沙场传送带下 等装满沙后再开走,为了提高效率,应该让运沙车边走边装沙。设想运沙车沿着固定的水平轨 道向前行驶沙子从传送带上匀速地竖直漏下,已知某时刻运沙车前进的速度为?,单位时间从 传送带上漏下的沙子质量为m,则下列说法正确的是() A.若轨道光滑测运沙车和漏进车的沙组成的系统动量守恒 B.若轨道光滑,则运沙车装的沙越来越多,速度却能保持不变 C.已知此时运沙车所受的轨道阻力为F瓢,则要维持运沙车匀速前进,运沙车的牵引力应为F 亲=F阳 D.己知此时运沙车所受的轨道阻力为F,则要维持运沙车匀速前进,运沙车的牵引力应为F *=F图+W 答案D 解析若轨道光滑,则运沙车和漏进车的沙组成的系统水平方向动量守恒,而不是总动量守恒, 因为沙子的竖直方向动量在变化,故选项A错误;设某时刻沙车总质量为m',随后一段时间△1
B.2.5 N C.25 N D.250 N 答案 C 解析设时间 t 内,落到雨伞上雨水的质量为 m,根据动量定理有 Ft=mv,m=ρvtπr 2 ,解得 F=ρv 2πr 2 ,代入数值解得 F=25 N,选项 C 正确。 5.一个质量为 0.18 kg 的垒球,以 25 m/s 的水平速度飞向球棒,被球棒打击后反向水平飞回,速 度大小变为 45 m/s,设球棒与垒球的作用时间为 0.01 s。下列说法正确的是 ( ) A.垒球的动量变化量大小为 3.6 kg·m/s B.球棒对垒球的冲量大小为 126 N·s C.球棒对垒球的平均作用力大小为 1 260 N D.球棒对垒球做的功为 36 J 答案 C 解析设垒球的初速度 v0=25 m/s 的方向为正方向,则末速度为 v1=-45 m/s,动量的变化量 Δp=mv1-mv0=-12.6 kg·m/s,即垒球的动量变化量大小为 12.6 kg·m/s,故选项 A 错误;由动量定 理 I=Δp 可知,球棒对垒球的冲量大小为 12.6 N·s,故选项 B 错误;由冲量的定义 I=Ft 可知,球 棒对垒球的平均作用力大小为𝐹 = Δ𝑝 𝑡 =1 260 N,故选项 C 正确;球棒对垒球作用的过程,由动 能定理可知,球棒对垒球做的功为 W=1 2 𝑚𝑣1 2 − 1 2 𝑚𝑣0 2=126 J,故选项 D 错误。 6.如图所示,光滑的四分之一圆弧轨道质量为 m',静止在光滑水平面上,一个质量为 m 的物块 在水平地面上以大小为 v0 的初速度向右运动并无能量损失地滑上圆弧轨道,当物块运动到圆 弧轨道上某一位置时,物块向上的速度为零,此时物块与圆弧轨道的动能之比为 1∶2,则此时 物块的动能与重力势能之比为(以地面为参考平面)( ) A.1∶2 B.1∶3 C.1∶6 D.1∶9 答案 C 解析因为水平面光滑,轨道和物块组成的系统水平方向动量守恒,当物块向上的速度为零时, 两物体速度相同,又因为此时物块与圆弧轨道的动能之比为 1∶2,即 1 2 mv2∶ 1 2 m'v2=1∶2,得到 m∶m'=1∶2;根据动量守恒定律有 mv0=(m+m')v,得到 v0=3v,根据能量守恒定律有1 2 𝑚𝑣0 2 = 1 2 (m+m')v 2+Ep,解得 Ep= 1 3 𝑚𝑣0 2 ,此时物块的动能为 Ek= 1 2 mv2= 1 18 𝑚𝑣0 2 ,所以此时物块的动能与 重力势能之比为 1∶6,故选项 C 正确,A、B、D 错误。 7.一辆运沙车按着大喇叭轰隆隆地从旁边开过,小明想,装沙时运沙车都是停在沙场传送带下, 等装满沙后再开走,为了提高效率,应该让运沙车边走边装沙。设想运沙车沿着固定的水平轨 道向前行驶,沙子从传送带上匀速地竖直漏下,已知某时刻运沙车前进的速度为 v,单位时间从 传送带上漏下的沙子质量为 m,则下列说法正确的是( ) A.若轨道光滑,则运沙车和漏进车的沙组成的系统动量守恒 B.若轨道光滑,则运沙车装的沙越来越多,速度却能保持不变 C.已知此时运沙车所受的轨道阻力为 F 阻,则要维持运沙车匀速前进,运沙车的牵引力应为 F 牵=F 阻 D.已知此时运沙车所受的轨道阻力为 F 阻,则要维持运沙车匀速前进,运沙车的牵引力应为 F 牵=F 阻+mv 答案 D 解析若轨道光滑,则运沙车和漏进车的沙组成的系统水平方向动量守恒,而不是总动量守恒, 因为沙子的竖直方向动量在变化,故选项 A 错误;设某时刻沙车总质量为 m',随后一段时间 Δt

内漏进沙车的沙子质量为△m,则由水平方向动量守恒有mp+0=(m'+△m)加',可以看出沙车速 度会逐渐减小,故选项B错误;选一段极短时间△1内漏进沙车的沙子△m为研究对象,由动量 定理,得FA1=Am0,车对漏进未的沙子向前的作用力为F=m,则以沙车为研究对象,由 平衡条件有F-F-F'=0,其中F是漏进来的沙子对车的阻力,由牛顿第三定律有F=F,联立 得F◆=Fm+mm,故选项C错误,D正确。 8.有关实际生活中的现象,下列说法正确的是( A.火箭靠喷出气流的反冲作用而获得巨大的速度 B.体操运动员在着地时屈腿是为了减小地面对运动员的冲量 C.用枪射击时要用肩部抵住枪身是为了减小反冲的影响 D.为了减轻撞车时对司乘人员的伤害,汽车前部安装气囊是为了减小司乘人员动量的变化量 答案AC 解析火箭靠喷出气流的反冲作用而获得巨大的速度,选项A正确:体操运动员在着地时屈腿 可以延长着地时间,从而可以减小地面对运动员的作用力,选项B错误;用枪射击时用肩部抵 住枪身可以防止枪身快速后退,故是为了减少反冲的影响,选项C正确;撞车时司乘人员动量 的变化量是确定的,由F1=△p可知,延长碰撞的时间可减小作用力,选项D错误。 9.如图所示,在质量为m的小车中挂着一个质量为的小球,小车(含小球)以恒定的速度u沿 光滑的水平面运动,与位于正对面的质量为m的静止木块发生碰撞,碰撞时间极短,在此碰撞 进行的过程中,下列说法可能正确的是 () A.小车、木块、小球的速度都发生变化,分别变为1、2、3,满足(m'+mo)u=mv1+mw2+o? B.小球的速度不变,小车和木块的速度变为1和2,满足m'u=mv1+m C.小球的速度不变,小车和木块的速度变为,满足m'u=(m'+m)v D.小车和小球的速度都变为1,木块的速度为2,满足(m'+mo)u=(m'+mo)v1+m2 答案BC 解析碰撞时间极短,所以小球相对小车没有发生摆动,即线对球的作用力原来是竖直向上的 现在还是竖直向上的.没有水平方向的分力,未玫变小球的动量即小球的速度不发生变化,故 选项A、D错误;因为小球的速度不变,所以研究对象选取小车和木块所构成的系统,系统水 平方向动量守恒,由动量守恒定律得m'u=m1+2,由于题目中并没有提供在碰撞过程中的 能量变化关系,所以也有可能小车和木块发生碰撞后以同一速度运动,即m'u=(m'+m)y,故选项 B、C正确。 10.如图所示,A、B两物体质量之比mA:B=3:2,原来静止在足够长的平板小车C上,A、B 间有一根被压缩的弹簧,水平地面光滑,在弹簧突然释放后很短时间内,下列说法正确的是 () AWB 为C (●) (● 7 A若A、B与平板车上表面间的动摩擦因数相同,A、B组成的系统动量守恒 B.若A、B与平板车上表面间的动摩擦因数相同,A、B、C组成的系统动量守恒 C若A、B所受的摩擦力大小相等,A、B组成的系统动量守恒 D.若A、B所受的摩擦力大小相等,A、B、C组成的系统动量守恒 答案BCD 解析如果A、B与平板车上表面间的动摩擦因数相同,弹簧释放后,A、B分别相对于小车向 左、向右滑动,它们所受的滑动摩擦力Fa向右,FB向左。由于m,mB=3,2,所以FA F细=3:2,则A、B组成的系统所受的外力之和不为零,故其动量不守恒,选项A错误。对 A、B、C组成的系统,A、B与C间的摩擦力为内力,该系统所受的外力为竖直方向上的重 力和支持力,它们的合力为零,故该系统的动量守恒,选项B、D正确。若A、B所受摩擦力大 小相等,则A、B组成的系统所受的外力之和为零,故其动量守恒,选项C正确。 二、实验题(共3小题,共18分)
内漏进沙车的沙子质量为 Δm,则由水平方向动量守恒有 m'v+0=(m'+Δm)v',可以看出沙车速 度会逐渐减小,故选项 B 错误;选一段极短时间 Δt 内漏进沙车的沙子 Δm 为研究对象,由动量 定理,得 FΔt=Δmv-0,车对漏进来的沙子向前的作用力为 F=Δ𝑚 Δ𝑡 v=mv,则以沙车为研究对象,由 平衡条件有 F 牵-F 阻-F'=0 ,其中 F'是漏进来的沙子对车的阻力,由牛顿第三定律有 F'=F,联立 得 F 牵=F 阻+mv,故选项 C 错误,D 正确。 8.有关实际生活中的现象,下列说法正确的是( ) A.火箭靠喷出气流的反冲作用而获得巨大的速度 B.体操运动员在着地时屈腿是为了减小地面对运动员的冲量 C.用枪射击时要用肩部抵住枪身是为了减小反冲的影响 D.为了减轻撞车时对司乘人员的伤害,汽车前部安装气囊是为了减小司乘人员动量的变化量 答案 AC 解析火箭靠喷出气流的反冲作用而获得巨大的速度,选项 A 正确;体操运动员在着地时屈腿 可以延长着地时间,从而可以减小地面对运动员的作用力,选项 B 错误;用枪射击时用肩部抵 住枪身可以防止枪身快速后退,故是为了减少反冲的影响,选项 C 正确;撞车时司乘人员动量 的变化量是确定的,由 Ft=Δp 可知,延长碰撞的时间可减小作用力,选项 D 错误。 9.如图所示,在质量为 m'的小车中挂着一个质量为 m0 的小球,小车(含小球)以恒定的速度 u 沿 光滑的水平面运动,与位于正对面的质量为 m 的静止木块发生碰撞,碰撞时间极短,在此碰撞 进行的过程中,下列说法可能正确的是 ( ) A.小车、木块、小球的速度都发生变化,分别变为 v1、v2、v3,满足(m'+m0)u=m'v1+mv2+m0v3 B.小球的速度不变,小车和木块的速度变为 v1 和 v2,满足 m'u=m'v1+mv2 C.小球的速度不变,小车和木块的速度变为 v,满足 m'u=(m'+m)v D.小车和小球的速度都变为 v1,木块的速度为 v2,满足(m'+m0)u=(m'+m0)v1+mv2 答案 BC 解析碰撞时间极短,所以小球相对小车没有发生摆动,即线对球的作用力原来是竖直向上的, 现在还是竖直向上的,没有水平方向的分力,未改变小球的动量,即小球的速度不发生变化,故 选项 A、D 错误;因为小球的速度不变,所以研究对象选取小车和木块所构成的系统,系统水 平方向动量守恒,由动量守恒定律得 m'u=m'v1+mv2,由于题目中并没有提供在碰撞过程中的 能量变化关系,所以也有可能小车和木块发生碰撞后以同一速度运动,即 m'u=(m'+m)v,故选项 B、C 正确。 10.如图所示,A、B 两物体质量之比 mA∶mB=3∶2,原来静止在足够长的平板小车 C 上,A、B 间有一根被压缩的弹簧,水平地面光滑,在弹簧突然释放后很短时间内,下列说法正确的是 ( ) A.若 A、B 与平板车上表面间的动摩擦因数相同,A、B 组成的系统动量守恒 B.若 A、B 与平板车上表面间的动摩擦因数相同,A、B、C 组成的系统动量守恒 C.若 A、B 所受的摩擦力大小相等,A、B 组成的系统动量守恒 D.若 A、B 所受的摩擦力大小相等,A、B、C 组成的系统动量守恒 答案 BCD 解析如果 A、B 与平板车上表面间的动摩擦因数相同,弹簧释放后,A、B 分别相对于小车向 左、向右滑动,它们所受的滑动摩擦力 FfA 向右,FfB向左。由于 mA∶mB=3∶2,所以 FfA∶ FfB=3∶2,则 A、B 组成的系统所受的外力之和不为零,故其动量不守恒,选项 A 错误。对 A、B、C 组成的系统,A、B 与 C 间的摩擦力为内力,该系统所受的外力为竖直方向上的重 力和支持力,它们的合力为零,故该系统的动量守恒,选项 B、D 正确。若 A、B 所受摩擦力大 小相等,则 A、B 组成的系统所受的外力之和为零,故其动量守恒,选项 C 正确。 二、实验题(共 3 小题,共 18 分)

11.(6分)小明做探究碰撞中的不变量实验的装置如图甲所示,悬挂在O点的单摆由长为1的 细线和直径为d的小球A组成,小球A与放置在光滑支撑杆上的直径相同的小球B发生对 心碰撞,碰后小球A继续摆动,小球B做平抛运动。 0 4cm uulu山uu mmmmm 10 20 甲 (1)小明用游标卡尺测小球A直径如图乙所示,则d= mm (2)又测得了小球A的质量m1,细线长度1,碰撞前小球A拉起的角度α和碰撞后小球B做平 抛运动的水平位移x、竖直下落高度h。为完成实验,还需要测量的物理量 答案1)14.40 (2)小球B的质量碰后小球A摆动的最大角B 解析1)由题图所示游标卡尺可知,球的直径d-14mm+8×0.05mm=14.40mm。 (2)小球A下摆过程机械能守恒,由机械能守恒定律得m1g(1-Cos)-m1v12,碰撞后仍可根据 机械能守恒定律计算小球A的速度,所以需要小球A碰后摆动的最大角B,小球B碰撞后做 平抛运动,根据平抛运动规律可得小球B的速度,要求小球B的动量,所以需要测量小球B的 质量2。 12.(6分)如图所示,用图示装置可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞 前后的动量关系。 D (1)实验中,直接测定小球碰撞前后的速度是不容易的,但是可以通过仅测量 (填选项 前的字母),间接地解决这个问题。 A.小球开始释放的高度h B.小球抛出点距地面的高度H C.小球做平抛运动的水平位移 (2)用天平测量两个小球的质量m1、2。图中O点是小球抛出点在水平地面上的垂直投 影。实验时,先让入射球m1多次从斜轨上S位置静止释放,然后,把被碰小球2静止于轨道 水平部分的末端,再将入射小球m1从斜轨上S位置静止释放,与小球2相撞,并多次重复:分 别找到小球的平均落点M、P、N,并测量出平均水平位移loM、loP、loN。 (3)若两球相碰前后的动量守恒,其表达式可表示为 [用(2)中测量的量表示]:若碰撞是弹性碰撞,那么还应满足的表达式为 [用(2)中测量的量表示]。 (1)C (3)mlop-mlox+mzlow mlop2-mloM2+mloN2 解析1)在该实验中,通过落地高度不变情况下水平射程来体现速度,故选项C正确。 (3)若两球相碰前后的动量守恒,则m1o=m1v1+m2,又loP=ol,loM=vl,loN=l,代入得 mlop=mloM+mlox若碰撞是弹性碰撞,满足能量守恒,有m1v02=mu12+mv2,代入得 mlop2=mloM2+mloN2。 13.(6分)在验证动量守恒定律实验中,装置如图所示,按照以下步骤进行操作: ①在平木板表面钉上白纸和复写纸,并将该木板竖直立于紧靠槽口处,使小球从斜槽轨道上 由静止释放,撞到木板并在白纸上留下痕迹O: ②将木板水平向右移动一定距离并固定,再使小球由静止释放,撞到木板上得到痕迹B:
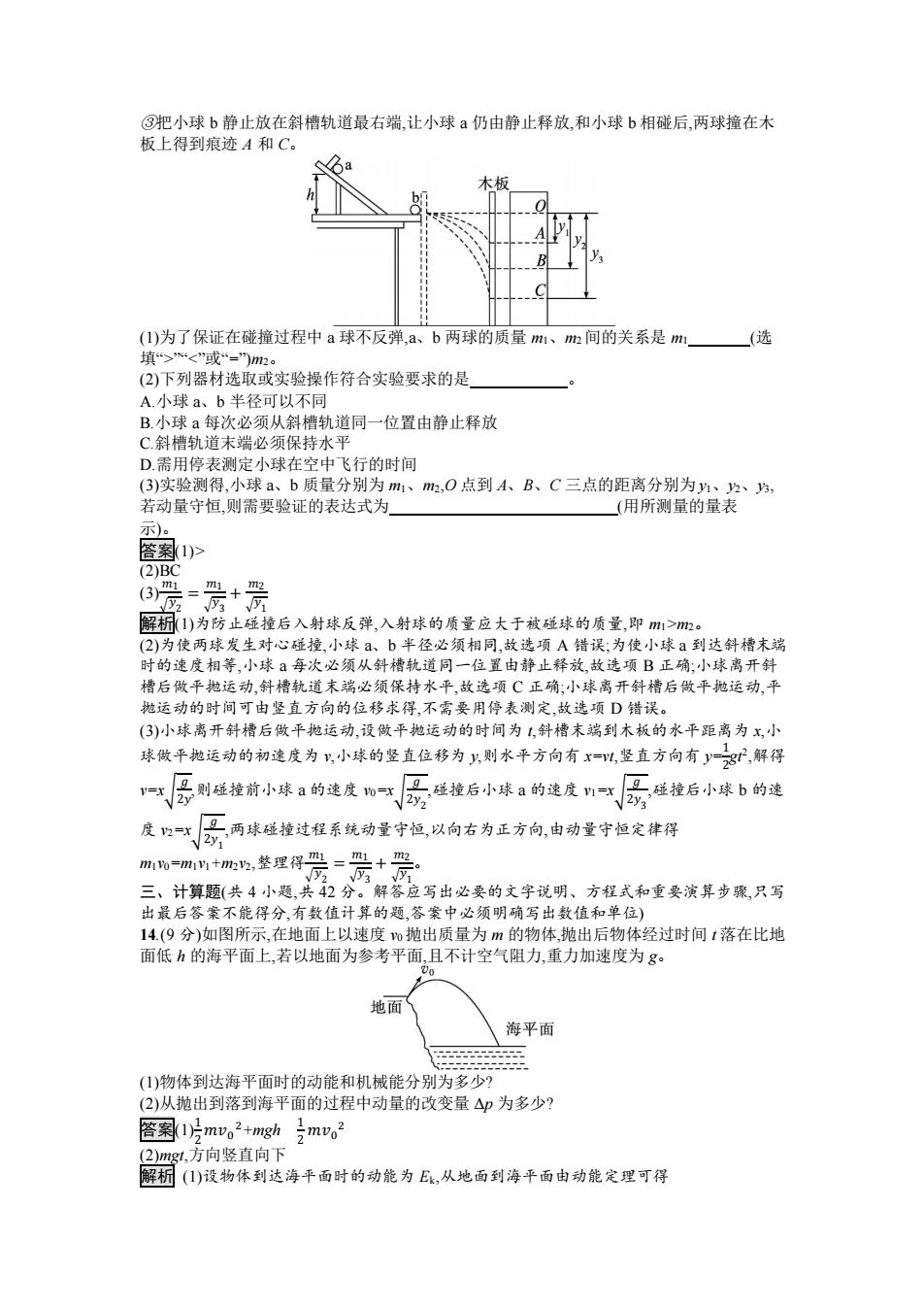
11.(6 分)小明做探究碰撞中的不变量实验的装置如图甲所示,悬挂在 O 点的单摆由长为 l 的 细线和直径为 d 的小球 A 组成,小球 A 与放置在光滑支撑杆上的直径相同的小球 B 发生对 心碰撞,碰后小球 A 继续摆动,小球 B 做平抛运动。 (1)小明用游标卡尺测小球 A 直径如图乙所示,则 d= mm。 (2)又测得了小球 A 的质量 m1,细线长度 l,碰撞前小球 A 拉起的角度 α 和碰撞后小球 B 做平 抛运动的水平位移 x、竖直下落高度 h。为完成实验,还需要测量的物理量 有 、 。 答案(1)14.40 (2)小球 B 的质量 m2 碰后小球 A 摆动的最大角 β 解析(1)由题图所示游标卡尺可知,球的直径 d=14 mm+8×0.05 mm=14.40 mm。 (2)小球 A 下摆过程机械能守恒,由机械能守恒定律得 m1gl(1-cos α)= 1 2 m1𝑣1 2 ,碰撞后仍可根据 机械能守恒定律计算小球 A 的速度,所以需要小球 A 碰后摆动的最大角 β;小球 B 碰撞后做 平抛运动,根据平抛运动规律可得小球 B 的速度,要求小球 B 的动量,所以需要测量小球 B 的 质量 m2。 12.(6 分)如图所示,用图示装置可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞 前后的动量关系。 (1)实验中,直接测定小球碰撞前后的速度是不容易的,但是可以通过仅测量 (填选项 前的字母),间接地解决这个问题。 A.小球开始释放的高度 h B.小球抛出点距地面的高度 H C.小球做平抛运动的水平位移 (2)用天平测量两个小球的质量 m1、m2。图中 O 点是小球抛出点在水平地面上的垂直投 影。实验时,先让入射球 m1 多次从斜轨上 S 位置静止释放;然后,把被碰小球 m2 静止于轨道 水平部分的末端,再将入射小球 m1 从斜轨上 S 位置静止释放,与小球 m2 相撞,并多次重复;分 别找到小球的平均落点 M、P、N,并测量出平均水平位移 lOM、lOP、lON。 (3)若两球相碰前后的动量守恒,其表达式可表示为 [用(2)中测量的量表示];若碰撞是弹性碰撞,那么还应满足的表达式为 [用(2)中测量的量表示]。 答案(1)C (3)m1lOP=m1lOM+m2lON m1𝑙𝑂𝑃 2 =m1𝑙𝑂𝑀 2+m2𝑙𝑂𝑁 2 解析(1)在该实验中,通过落地高度不变情况下水平射程来体现速度,故选项 C 正确。 (3)若两球相碰前后的动量守恒,则 m1v0=m1v1+m2v2,又 lOP=v0t,lOM=v1t,lON=v2t,代入得 m1lOP=m1lOM+m2lON;若碰撞是弹性碰撞,满足能量守恒,有 1 2 m1𝑣0 2 = 1 2 m1𝑣1 2 + 1 2 m2𝑣2 2 ,代入得 m1𝑙𝑂𝑃 2 =m1𝑙𝑂𝑀 2+m2𝑙𝑂𝑁 2。 13.(6 分)在验证动量守恒定律实验中,装置如图所示,按照以下步骤进行操作: ①在平木板表面钉上白纸和复写纸,并将该木板竖直立于紧靠槽口处,使小球 a 从斜槽轨道上 由静止释放,撞到木板并在白纸上留下痕迹 O; ②将木板水平向右移动一定距离并固定,再使小球 a 由静止释放,撞到木板上得到痕迹 B;
③把小球b静止放在斜槽轨道最右端,让小球a仍由静止释放,和小球b相碰后,两球撞在木 板上得到痕迹A和C。 板 (I)为了保证在碰撞过程中a球不反弹,a、b两球的质量m1、m间的关系是m (选 填“>% (2)BC 8暖-芳+器 解1)为防止碰撞后入射球反弹,入射球的质量应大于被碰球的质量,即m1>m。 (2)为使两球发生对心碰撞,小球a、b半径必须相同,故选项A错误;为使小球a到达斜槽末端 时的速度相等,小球每次必须从斜槽轨道同一位置由静止释放,故选项B正确;小球离开斜 槽后做平抛运动,斜槽轨道末端必须保持水平,故选项C正确;小球离开斜槽后做平抛运动,平 抛运动的时间可由竖直方向的位移求得,不需要用停表测定,故选项D错误。 (3)小球离开斜槽后做平抛运动,设做平抛运动的时间为1,斜槽末端到木板的水平距离为x,小 球做平抛运动的初速度为书小球的竖直位移为则水平方向有x=以,竖直方向有y3,解得 区则碰撞前小球a的速度w=r 三碰撞后小球a的速度1=x氏碰撞后小球b的速 2y3 度2=x :,两球碰撞过程系统动量守恒,以向右为正方向,由动量守恒定律得 2y1 m1%=m1M+m22,整理得严 三、计算题(共4小题,共42分。解答应写出必要的文字说明、方程式和重要演算步骤,只写 出最后答案不能得分,有数值计算的题,答案中必须明确写出数值和单位) 14.(9分)如图所示,在地面上以速度o抛出质量为m的物体,抛出后物体经过时间1落在比地 面低h的海平面上,若以地面为参考平面,且不计空气阻力,重力加速度为g。 地面 海平面 -22 (1)物体到达海平面时的动能和机械能分别为多少? (2)从抛出到落到海平面的过程中动量的改变量△p为多少? 管案12mvo2+mgh2mvo2 (2)mg4,方向竖直向下 解析 ()设物体到达海平面时的动能为E,从地面到海平面由动能定理可得
③把小球 b 静止放在斜槽轨道最右端,让小球 a 仍由静止释放,和小球 b 相碰后,两球撞在木 板上得到痕迹 A 和 C。 (1)为了保证在碰撞过程中 a 球不反弹,a、b 两球的质量 m1、m2 间的关系是 m1 (选 填“>”“ (2)BC (3) 𝑚1 √𝑦 2 = 𝑚1 √𝑦 3 + 𝑚2 √𝑦 1 解析(1)为防止碰撞后入射球反弹,入射球的质量应大于被碰球的质量,即 m1>m2。 (2)为使两球发生对心碰撞,小球 a、b 半径必须相同,故选项 A 错误;为使小球 a 到达斜槽末端 时的速度相等,小球 a 每次必须从斜槽轨道同一位置由静止释放,故选项 B 正确;小球离开斜 槽后做平抛运动,斜槽轨道末端必须保持水平,故选项 C 正确;小球离开斜槽后做平抛运动,平 抛运动的时间可由竖直方向的位移求得,不需要用停表测定,故选项 D 错误。 (3)小球离开斜槽后做平抛运动,设做平抛运动的时间为 t,斜槽末端到木板的水平距离为 x,小 球做平抛运动的初速度为 v,小球的竖直位移为 y,则水平方向有 x=vt,竖直方向有 y= 1 2 gt2 ,解得 v=x√ 𝑔 2𝑦 ,则碰撞前小球 a 的速度 v0=x√ 𝑔 2𝑦 2 ,碰撞后小球 a 的速度 v1=x√ 𝑔 2𝑦 3 ,碰撞后小球 b 的速 度 v2=x√ 𝑔 2𝑦 1 ,两球碰撞过程系统动量守恒,以向右为正方向,由动量守恒定律得 m1v0=m1v1+m2v2,整理得 𝑚1 √𝑦 2 = 𝑚1 √𝑦 3 + 𝑚2 √𝑦 1 。 三、计算题(共 4 小题,共 42 分。解答应写出必要的文字说明、方程式和重要演算步骤,只写 出最后答案不能得分,有数值计算的题,答案中必须明确写出数值和单位) 14.(9 分)如图所示,在地面上以速度 v0 抛出质量为 m 的物体,抛出后物体经过时间 t 落在比地 面低 h 的海平面上,若以地面为参考平面,且不计空气阻力,重力加速度为 g。 (1)物体到达海平面时的动能和机械能分别为多少? (2)从抛出到落到海平面的过程中动量的改变量 Δp 为多少? 答案(1)1 2 𝑚𝑣0 2+mgh 1 2 𝑚𝑣0 2 (2)mgt,方向竖直向下 解析 (1)设物体到达海平面时的动能为 Ek,从地面到海平面由动能定理可得

mgh-Ex-mvo2 解得Ek=7mvo2+mg 因为抛出过程中机械能守恒,则 E4=E地子mv2。 (2)从抛出到落入海平面由动量定理可得△p==mg,方向竖直向下。 15.(9分)如图所示,一质量为m'=4m的物块(可视为质点)静止在光滑水平桌面的边缘,桌面离 水平面的高度为。一质量为m的子弹以水平速度%射入物块后,以水平速度空射出,物块落 地后不反弹,重力加速度为g。求: 777777777777777777777 (1)子弹射入物块的过程中系统损失的机械能: (2)物块落地点与抛出点的距离。 含案1日mv2 a2+爵 解标(1)子弹射穿木块过程动量守恒 mw=m学+mn 解得 系统损失的机械能 cmw2-m()2+号m 解得△E品m2. (2)木块做平抛运动x=1 h-r s=vx2 +h2 解得s=h2+如五 18g1 16.(12分)如图所示,物体A静止在光滑平直轨道上,其左端固定有轻质弹簧,物体B以速度 0=3.0m/s沿轨道向物体A运动,并通过弹簧与物体A发生相互作用,己知A的质量为mA=2 kg,B的质量为mB=1kg。 00 B (1)当物体A的速度多大时,A、B组成的系统动能损失最大?损失的最大动能为多少? (2)弹簧恢复原长时,物体A和物体B的速度分别为多少? 答案1)1ms3J (2)2m/s,方向与B初速度方向相同;1m/s,方向与B初速度方向相反 解析1)当两物体速度相等时,弹簧压缩量最大,系统损失的动能最大。以B的初速度方向为 正方向,由动量守恒定律知 B'o=气mA+B)v 解得v=1m/s 损失的动能为 △Ek2iev2-2×(mA+mB)2-3J。 (2)由动量守恒定律知 I1Bo=1AVA十IBVB
mgh=Ek- 1 2 𝑚𝑣0 2 解得 Ek= 1 2 𝑚𝑣0 2+mgh 因为抛出过程中机械能守恒,则 E 海=E 地= 1 2 𝑚𝑣0 2。 (2)从抛出到落入海平面由动量定理可得 Δp=I=mgt,方向竖直向下。 15.(9 分)如图所示,一质量为 m'=4m 的物块(可视为质点)静止在光滑水平桌面的边缘,桌面离 水平面的高度为 h。一质量为 m 的子弹以水平速度 v0 射入物块后,以水平速度𝑣0 3 射出,物块落 地后不反弹,重力加速度为 g。求: (1)子弹射入物块的过程中系统损失的机械能; (2)物块落地点与抛出点的距离。 答案(1) 7 18 𝑚𝑣0 2 (2)√ℎ 2 + 𝑣0 2ℎ 18𝑔 解析(1)子弹射穿木块过程动量守恒 mv0=m· 𝑣0 3 +m'v 解得 v= 𝑣0 6 系统损失的机械能 ΔE=1 2 𝑚𝑣0 2 − [ 1 2 𝑚 ( 𝑣0 3 ) 2 + 1 2 𝑚'𝑣 2] 解得 ΔE= 7 18𝑚𝑣0 2。 (2)木块做平抛运动 x=vt h=1 2 gt2 s=√𝑥 2 + ℎ 2 解得 s=√ℎ 2 + 𝑣0 2ℎ 18𝑔 。 16.(12 分)如图所示,物体 A 静止在光滑平直轨道上,其左端固定有轻质弹簧,物体 B 以速度 v0=3.0 m/s 沿轨道向物体 A 运动,并通过弹簧与物体 A 发生相互作用,已知 A 的质量为 mA=2 kg,B 的质量为 mB=1 kg。 (1)当物体 A 的速度多大时,A、B 组成的系统动能损失最大?损失的最大动能为多少? (2)弹簧恢复原长时,物体 A 和物体 B 的速度分别为多少? 答案(1)1 m/s 3 J (2)2 m/s,方向与 B 初速度方向相同;1 m/s,方向与 B 初速度方向相反 解析(1)当两物体速度相等时,弹簧压缩量最大,系统损失的动能最大。以 B 的初速度方向为 正方向,由动量守恒定律知 mBv0=(mA+mB)v 解得 v=1 m/s 损失的动能为 ΔEk= 1 2 mB𝑣0 2 − 1 2 ×(mA+mB)v 2=3 J。 (2)由动量守恒定律知 mBv0=mAvA+mBvB

由机械能守恒得 MBVo2 =mAVA2+maVg2 解得阳=-1m/s,方向与B初速度方向相反;vA=2m/s,方向与B初速度方向相同。 17.(12分)如图所示,装置的左边是足够长的光滑水平台面,一轻质弹簧左端固定,右端连接着 质量m'-3kg的小物块A。装置的中间是水平传送带,它与左右两边的台面等高,并能平滑对 接。传送带始终以v=3ms的速度逆时针转动。装置的右边是一段光滑的与水平台面连接 的光滑曲面,质量m=1kg的小物块B从其上距水平台面h=1.0m处由静止释放。己知物块 B与传送带之间的动摩擦因数u=0.2,传送带的长度I=1.0m,设物块A、B之间发生的是对心 弹性碰撞,第一次碰撞前物块A静止且处于平衡状态,g取10/s2。 B v=3 m/s (】 (1)求物块B与物块A第一次碰撞前的速度大小。 (2)求物块B与物块A第一次碰撞后到再次碰撞前与传送带的摩擦生热。 (3)如果物块A、B每次碰撞后,物块A再回到平衡位置时都会立即被锁定,而当它们再次碰 撞前锁定被解除,试求出物块B第6次碰撞后运动的速度大小。 答1)4m/s (2)12J (3)0.0625m/s 解析1)设B滑到曲面底部速度为0,根据机械能守恒定律得 mghmvo2 解得o=√2gh=2V5m/s 由于w>v=3s,B在传送带上开始做匀减速运动,设B一直减速滑过传送带的速度为v1,由 动能定理可得 -umgl-7mv;2-mvo2 解得v=4m/s 由于1=4m/s仍大于3m/s,说明假设成立,即B与A碰前速度为4m/s。 (2)设第一次碰后A的速度为vA1,B的速度为B1,取向左为正方向,根据动量守恒定律和机械 能守恒定律得 mvI=mVB1+m'VAI mu2=左mvs12+2nv2 解得=之-2ms 上式表明B碰后以2s的速度向右反弹,滑上传送带后在摩擦力的作用下减速,设向左减速 的最大位移为,由动能定理得 -MmgxB-0-7mvB12 解得xB=1m 因阳==1.0m,B刚好滑到传送带右端再原速率返回左端,在传送带上的运动时间121=25 -4g B在传送带上运动的过程中,与传送带的摩擦生热 Q=ug(vt-0)=12J。 (3)由(2)中的关系可知第二次碰后B仍然反弹,且碰后速度大小仍为B碰前的即 同理可推,B每次碰后都将被传送带带回与A发生下一次碰撞,则B与A碰撞次后反弹,速 度大小为头m/s,B第6次碰撞后的速度大小为0.0625ms
由机械能守恒得 1 2 mB𝑣0 2 = 1 2 mA𝑣A 2 + 1 2 mB𝑣B 2 解得 vB=-1 m/s,方向与 B 初速度方向相反;vA=2 m/s,方向与 B 初速度方向相同。 17.(12 分)如图所示,装置的左边是足够长的光滑水平台面,一轻质弹簧左端固定,右端连接着 质量 m'=3 kg 的小物块 A。装置的中间是水平传送带,它与左右两边的台面等高,并能平滑对 接。传送带始终以 v=3 m/s 的速度逆时针转动。装置的右边是一段光滑的与水平台面连接 的光滑曲面,质量 m=1 kg 的小物块 B 从其上距水平台面 h=1.0 m 处由静止释放。已知物块 B 与传送带之间的动摩擦因数 μ=0.2,传送带的长度 l=1.0 m,设物块 A、B 之间发生的是对心 弹性碰撞,第一次碰撞前物块 A 静止且处于平衡状态,g 取 10 m/s2。 (1)求物块 B 与物块 A 第一次碰撞前的速度大小。 (2)求物块 B 与物块 A 第一次碰撞后到再次碰撞前与传送带的摩擦生热。 (3)如果物块 A、B 每次碰撞后,物块 A 再回到平衡位置时都会立即被锁定,而当它们再次碰 撞前锁定被解除,试求出物块 B 第 6 次碰撞后运动的速度大小。 答案(1)4 m/s (2)12 J (3)0.062 5 m/s 解析(1)设 B 滑到曲面底部速度为 v0,根据机械能守恒定律得 mgh=1 2 𝑚𝑣0 2 解得 v0=√2𝑔ℎ=2√5 m/s 由于 v0>v=3 m/s,B 在传送带上开始做匀减速运动,设 B 一直减速滑过传送带的速度为 v1,由 动能定理可得 -μmgl=1 2 𝑚𝑣1 2 − 1 2 𝑚𝑣0 2 解得 v1=4 m/s 由于 v1=4 m/s 仍大于 3 m/s,说明假设成立,即 B 与 A 碰前速度为 4 m/s。 (2)设第一次碰后 A 的速度为 vA1,B 的速度为 vB1,取向左为正方向,根据动量守恒定律和机械 能守恒定律得 mv1=mvB1+m'vA1 1 2 𝑚𝑣1 2 = 1 2 𝑚𝑣B1 2 + 1 2 m'𝑣A1 2 解得 vB1=- 𝑣1 2 =-2 m/s 上式表明 B 碰后以 2 m/s 的速度向右反弹,滑上传送带后在摩擦力的作用下减速,设向左减速 的最大位移为 xB,由动能定理得 -μmgxB=0- 1 2 𝑚𝑣B1 2 解得 xB=1 m 因 xB=l=1.0 m,B 刚好滑到传送带右端再原速率返回左端,在传送带上的运动时间 t= 2𝑣B1 -𝜇𝑔 =2 s B 在传送带上运动的过程中,与传送带的摩擦生热 Q=μmg(𝑣𝑡-0)=12 J。 (3)由(2)中的关系可知第二次碰后 B 仍然反弹,且碰后速度大小仍为 B 碰前的1 2 ,即 vB2= 1 2 vB1=- 𝑣1 2 2=- 4 2 2 m/s 同理可推,B 每次碰后都将被传送带带回与 A 发生下一次碰撞,则 B 与 A 碰撞 n 次后反弹,速 度大小为 4 2 𝑛 m/s,B 第 6 次碰撞后的速度大小为 0.062 5 m/s