
第八章过关检测 (时间:90分钟满分:100分) 一、选择题(共10小题,每小题4分,共40分。在每小题给出的四个选项中,第 1~7小题只有一个选项符合题目要求,第8~10小题有多个选项符合题目要求,全 部选对的得4分,选对但不全的得2分,有选错或不答的得0分) 1.背越式跳高是一项跳跃障碍的运动项目,包括助跑、起跳、过杆和落地四个阶 段,下图为从起跳到落地的运动过程分解图,某同学身高1.80m,体重60kg,参加学 校运动会成功地越过了1.90m的横杆,该同学跳起时刻的动能可能是(g取10 m/s2)() A.400J B.500J C.800J D.2000J 答案:C 解析:运动员跳高过程可以看作竖直上抛运动,当重心达到足以越过横杆时速度恰 好为零,运动员重心升高高度约为h=1.90m2”m=1.0m 根据机械能守恒定律可知,跳起时的动能 Ek=mgh=60×10×1.0J=600J 因实际过程中存在阻力,则可知,只有动能大于600J时才能成功越过,但2000J 不符合实际,选项C正确,A、B、D错误。 2.某运动员在比赛时投掷铅球的分解动作如图所示,若铅球出手时速度大小约为 10/s,铅球质量为5kg,则在运动员掷铅球的过程中,合力对铅球做的功约为 () A.25J B.250J C.70J D.270J 答案B 解析:对掷铅球的过程,由动能定理得合力对铅球做的功为W-m2-0×5×102 J=250J。 3.如图所示,小物体A沿高为、倾角为0的光滑斜面以初速度o从顶端滑到底 端,而相同的物体B以同样大小的初速度从同等高度处竖直上抛,则( )
第八章过关检测 (时间:90 分钟 满分:100 分) 一、选择题(共 10 小题,每小题 4 分,共 40 分。在每小题给出的四个选项中,第 1~7 小题只有一个选项符合题目要求,第 8~10 小题有多个选项符合题目要求,全 部选对的得 4 分,选对但不全的得 2 分,有选错或不答的得 0 分) 1.背越式跳高是一项跳跃障碍的运动项目,包括助跑、起跳、过杆和落地四个阶 段,下图为从起跳到落地的运动过程分解图,某同学身高 1.80 m,体重 60 kg,参加学 校运动会成功地越过了 1.90 m 的横杆,该同学跳起时刻的动能可能是(g 取 10 m/s2 )( ) A.400 J B.500 J C.800 J D.2 000 J 答案:C 解析:运动员跳高过程可以看作竖直上抛运动,当重心达到足以越过横杆时速度恰 好为零,运动员重心升高高度约为 h=1.90 m- 1.80 2 m=1.0 m 根据机械能守恒定律可知,跳起时的动能 Ek=mgh=60×10×1.0 J=600 J 因实际过程中存在阻力,则可知,只有动能大于 600 J 时才能成功越过,但 2 000 J 不符合实际,选项 C 正确,A、B、D 错误。 2.某运动员在比赛时投掷铅球的分解动作如图所示,若铅球出手时速度大小约为 10 m/s,铅球质量为 5 kg,则在运动员掷铅球的过程中,合力对铅球做的功约为 ( ) A.25 J B.250 J C.70 J D.270 J 答案:B 解析:对掷铅球的过程,由动能定理得合力对铅球做的功为 W=1 2 𝑚𝑣0 2 -0= 1 2 ×5×102 J=250 J。 3.如图所示,小物体 A 沿高为 h、倾角为 θ 的光滑斜面以初速度 v0 从顶端滑到底 端,而相同的物体 B 以同样大小的初速度从同等高度处竖直上抛,则( )

A.两物体落地时速度相同 B.从开始至落地,重力对它们做功相同 C.两物体落地时重力的瞬时功率相同 D.从开始运动至落地过程中,重力对它们做功的平均功率相同 答案B 解析:整个过程重力对它们做的功均为mgh,根据机械能守恒知两物体落地时速度 的大小相等,但方向不同,选项A、C错误,B正确:从开始至落地它们用时不等,选 项D错误。 4.如图所示,某同学用绳子拉动木箱,使它从静止开始沿粗糙水平路面运动至具有 某一速度。木箱获得的动能一定( A.小于拉力所做的功 B.等于拉力所做的功 C.等于克服摩擦力所做的功 D.大于克服摩擦力所做的功 答案:A 解析:设拉力做的功、克服摩擦力做的功分别为WT、W,木箱获得的动能为Ek,根 据动能定理可知,WT-W=Ek,则Ek<WT,选项A正确。 5.从地面竖直向上抛出一物体,物体在运动过程中除受到重力外,还受到一大小不 变、方向始终与运动方向相反的外力作用。距地面高度h在3以内时,物体上 升、下落过程中动能Ek随h的变化如图所示。重力加速度取10/s2。该物体 的质量为() 60 48 24 12 3 h/m A.2 kg B.1.5 kg C.1kg D.0.5 kg 答案:C 解析:根据动能定理,物体在上升过程中有-mgh-Fh=Ek2-Ek1,其中Ek2=36J,Ek1=72 J,h=3 m
A.两物体落地时速度相同 B.从开始至落地,重力对它们做功相同 C.两物体落地时重力的瞬时功率相同 D.从开始运动至落地过程中,重力对它们做功的平均功率相同 答案:B 解析:整个过程重力对它们做的功均为 mgh,根据机械能守恒知两物体落地时速度 的大小相等,但方向不同,选项 A、C 错误,B 正确;从开始至落地它们用时不等,选 项 D 错误。 4.如图所示,某同学用绳子拉动木箱,使它从静止开始沿粗糙水平路面运动至具有 某一速度。木箱获得的动能一定( ) A.小于拉力所做的功 B.等于拉力所做的功 C.等于克服摩擦力所做的功 D.大于克服摩擦力所做的功 答案:A 解析:设拉力做的功、克服摩擦力做的功分别为 WT、Wf,木箱获得的动能为 Ek,根 据动能定理可知,WT-Wf=Ek,则 Ek<WT,选项 A 正确。 5.从地面竖直向上抛出一物体,物体在运动过程中除受到重力外,还受到一大小不 变、方向始终与运动方向相反的外力作用。距地面高度 h 在 3 m 以内时,物体上 升、下落过程中动能 Ek 随 h 的变化如图所示。重力加速度取 10 m/s2。该物体 的质量为( ) A.2 kg B.1.5 kg C.1 kg D.0.5 kg 答案:C 解析:根据动能定理,物体在上升过程中有-mgh-Fh=Ek2-Ek1,其中 Ek2=36 J,Ek1=72 J,h=3 m

在下落过程中有mgh-Fh=Ek4-Ek3,其中Ek3=24J,Ek4=48J,h=3m 联立求得m=1kg 6.如图所示,表面光滑的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并 跨过滑轮(不计滑轮的质量和轴摩擦)。初始时刻,A、B处于同一高度并恰好静 止。剪断轻绳后A下落、B沿斜面下滑则从剪断轻绳到物块着地,两物块() A.速率的变化量不同 B.机械能的变化量不同 C.重力势能的变化量相同 D.重力做功的平均功率相同 答案D 解析:剪断轻绳后,A做自由落体运动,B沿斜面做初速度为零的匀加速直线运动, 只有重力对两物块做功,根据机械能守恒定律得mgh=三2,解得v=√2gh,所以速 率的变化量为△v=v-0=√2gh,速率的变化量相同,故选项A错误;两物块都只有重 力做功,机械能守恒,所以机械能的变化量相同,均为零,故选项B错误:剪断轻绳 前,由平衡条件得mAg=megsin0,.故mB>mA,又h相同,所以重力势能的变化量 △Ep=mgh不同,故选项C错误;对A根据运动学公式得,A运动时间为A= 力做功的平均功率为PA=严A贮=mAgh, 品设B运动时间为a,则品。=n 0tg2,解得B=1 巫重力做功的平均功率为PB=mg必=meghsin0只,又 mAg=mBgsin 0,所以重力做功的平均功率相同,故选项D正确。 7.如图所示,一质量为m的光滑大圆环,用一细轻杆固定在竖直平面内:套在大环 上质量为m的小环(可视为质点),从大环的最高处由静止滑下。重力加速度大小 为8,当小环滑到大环的最低点时,大环对轻杆拉力的大小为( A.m'g-5mg B.m'g+mg C.m'g+5mg D.m'g+10mg 答案:C 解析:设小环到大环最低点的速度为v,由机械能守恒定律,得二mm2=mg2R① 小环在大环上做圆周运动,在最低点时,大环对它的支持力方向竖直向上,设为F、, 由牛顿第二定律,得mg=m片②
在下落过程中有 mgh-Fh=Ek4-Ek3,其中 Ek3=24 J,Ek4=48 J,h=3 m 联立求得 m=1 kg。 6.如图所示,表面光滑的固定斜面顶端安装一定滑轮,小物块 A、B 用轻绳连接并 跨过滑轮(不计滑轮的质量和轴摩擦)。初始时刻,A、B 处于同一高度并恰好静 止。剪断轻绳后 A 下落、B 沿斜面下滑,则从剪断轻绳到物块着地,两物块( ) A.速率的变化量不同 B.机械能的变化量不同 C.重力势能的变化量相同 D.重力做功的平均功率相同 答案:D 解析:剪断轻绳后,A 做自由落体运动,B 沿斜面做初速度为零的匀加速直线运动, 只有重力对两物块做功,根据机械能守恒定律得 mgh=1 2 mv2 ,解得 v=√2𝑔ℎ,所以速 率的变化量为 Δv=v-0=√2𝑔ℎ,速率的变化量相同,故选项 A 错误;两物块都只有重 力做功,机械能守恒,所以机械能的变化量相同,均为零,故选项 B 错误;剪断轻绳 前,由平衡条件得 mAg=mBgsin θ,故 mB>mA,又 h 相同,所以重力势能的变化量 ΔEp=mgh 不同,故选项 C 错误;对 A 根据运动学公式得,A 运动时间为 tA=√ 2ℎ 𝑔 ,重 力做功的平均功率为 PA= 𝑚A𝑔ℎ 𝑡 =mAgh√ 𝑔 2ℎ ,设 B 运动时间为 tB,则 ℎ sin𝜃 = 1 2 gsin θ·𝑡B 2 ,解得 tB= 1 sin𝜃 √ 2ℎ 𝑔 ,重力做功的平均功率为 PB= 𝑚B 𝑔ℎ 𝑡B =mBghsin θ√ 𝑔 2ℎ ,又 mAg=mBgsin θ,所以重力做功的平均功率相同,故选项 D 正确。 7.如图所示,一质量为 m'的光滑大圆环,用一细轻杆固定在竖直平面内;套在大环 上质量为 m 的小环(可视为质点),从大环的最高处由静止滑下。重力加速度大小 为 g,当小环滑到大环的最低点时,大环对轻杆拉力的大小为( ) A.m'g-5mg B.m'g+mg C.m'g+5mg D.m'g+10mg 答案:C 解析:设小环到大环最低点的速度为 v,由机械能守恒定律,得 1 2 mv2=mg·2R① 小环在大环上做圆周运动,在最低点时,大环对它的支持力方向竖直向上,设为 FN, 由牛顿第二定律,得 FN-mg=m 𝑣 2 𝑅 ②

由①②得FN=5mg,由牛顿第三定律可知,小环对大环竖直向下的压力 FN'=FN=5mg。大环平衡,轻杆对大环的拉力为F=Fv'+m'g=m'g+5mg,选项C正 确。 8.(2020天津卷)复兴号动车在世界上首次实现速度350kmh自动驾驶功能,成为 我国高铁自主创新的又一重大标志性成果。一列质量为m的动车,初速度为, 以恒定功率P在平直轨道上运动,经时间1达到该功率下的最大速度m,设动车行 驶过程所受到的阻力F保持不变。动车在时间1内() A.做匀加速直线运动 B.加速度逐渐减小 C.牵引力的功率P=Fvm D.牵引力做功W=之mvm2-m,2 答案BC 解析:动车的功率恒定,根据P=Fⅴ可知动车的牵引力减小,根据牛顿第二定律得 FF=ma,可知动车的加速度减小,所以动车做加速度减小的加速运动,选项A错 误,B正确;当加速度为0时,牵引力等于阻力,则额定功率为P=Fvm,选项C正确; 动车功率恒定,在1时间内,牵引力做功为W=P1,根据动能定理得P-Fs=mvm2- m2,选项D错误。 9.如图所示,轻质弹簧的左端固定,并处于自然状态。质量为m的物块,从A点向 左沿水平地面运动,压缩弹簧后被弹回,运动到A点恰好静止。物块向左运动的最 大距离为S,与地面间的动摩擦因数为4,重力加速度为g,弹簧未超出弹性限度。 在上述过程中() A.弹簧的最大弹力为umg B.物块克服摩擦力做的功为2umgs C.弹簧的最大弹性势能为umgs D.物块在A点的初速度为V2ugs 答案BC 解析:物块压缩弹簧最短时有F>ug,故选项A错误;全过程物块通过的路程为 2s,所以全过程中物块克服摩擦力做的功为W=umg2s,故选项B正确;物块从弹 簧压缩最短处到A点,由能量守恒得Epmax=umgs,故选项C正确;物块从A点返回 A点,由动能定理得-mg2s=0mv2,解得o=2√gs,故选项D错误
由①②得 FN=5mg,由牛顿第三定律可知,小环对大环竖直向下的压力 FN'=FN=5mg。大环平衡,轻杆对大环的拉力为 F=FN'+m'g=m'g+5mg,选项 C 正 确。 8.(2020·天津卷)复兴号动车在世界上首次实现速度 350 km/h 自动驾驶功能,成为 我国高铁自主创新的又一重大标志性成果。一列质量为 m 的动车,初速度为 v0, 以恒定功率 P 在平直轨道上运动,经时间 t 达到该功率下的最大速度 vm,设动车行 驶过程所受到的阻力 F 保持不变。动车在时间 t 内( ) A.做匀加速直线运动 B.加速度逐渐减小 C.牵引力的功率 P=Fvm D.牵引力做功 W=1 2 𝑚𝑣m 2 − 1 2 𝑚𝑣0 2 答案:BC 解析:动车的功率恒定,根据 P=F 牵 v 可知动车的牵引力减小,根据牛顿第二定律得 F 牵-F=ma,可知动车的加速度减小,所以动车做加速度减小的加速运动,选项 A 错 误,B 正确;当加速度为 0 时,牵引力等于阻力,则额定功率为 P=Fvm,选项 C 正确; 动车功率恒定,在 t 时间内,牵引力做功为 W=Pt,根据动能定理得 Pt-Fs=1 2 𝑚𝑣m 2 − 1 2 𝑚𝑣0 2 ,选项 D 错误。 9.如图所示,轻质弹簧的左端固定,并处于自然状态。质量为 m 的物块,从 A 点向 左沿水平地面运动,压缩弹簧后被弹回,运动到 A 点恰好静止。物块向左运动的最 大距离为 s,与地面间的动摩擦因数为 μ,重力加速度为 g,弹簧未超出弹性限度。 在上述过程中( ) A.弹簧的最大弹力为 μmg B.物块克服摩擦力做的功为 2μmgs C.弹簧的最大弹性势能为 μmgs D.物块在 A 点的初速度为√2𝜇𝑔𝑠 答案:BC 解析:物块压缩弹簧最短时有 F 弹>μmg,故选项 A 错误;全过程物块通过的路程为 2s,所以全过程中物块克服摩擦力做的功为 Wf=μmg·2s,故选项 B 正确;物块从弹 簧压缩最短处到 A 点,由能量守恒得 Epmax=μmgs,故选项 C 正确;物块从 A 点返回 A 点,由动能定理得-μmg·2s=0- 1 2 𝑚𝑣0 2 ,解得 v0=2√𝜇𝑔𝑠,故选项 D 错误

10.如图所示,三个小球A、B、C的质量均为m,A与B、C间通过铰链用轻杆连 接,杆长为1,B、C置于水平地面上,用一轻质弹簧连接,弹簧处于原长。现A由静 止释放下降到最低点,两轻杆间夹角a由60°变为120°,A、B、C在同一竖直 平面内运动,弹簧在弹性限度内,忽略一切摩擦,重力加速度为g。则在此过程中 () A.A的动能达到最大前,B受到地面的支持力小于三mg B.A的动能最大时,B受到地面的支持力等于mg C弹簧的弹性势能最大时,A的加速度方向竖直向下 D.弹簧的弹性势能最大值为mg 答案:AB 解析:A的动能最大时,设B和C受到地面的支持力大小均为F,此时A、B、C整 体在竖直方向受力平衡,可得2F=3mg,所以F-mg,A的动能达到最大前一直加 速下降,处于失重状态,所以B受到地面的支持力小于三g,故选项A、B正确:当 A达到最低,点时动能为零,此时弹簧的弹性势能最大,A的加速度方向向上,故选 项C错误;A球达到最大动能后向下做减速运动,到达最低点时三个小球的动能 均为零,由机械能守恒定律得,弹簧的弹性势能为Ep=mg(cos30°cos 60°)=1mgl,故选项D错误。 二、实验题(共2小题,共16分) 11.(8分)2020全国卷0某同学利用图甲所示装置验证动能定理。调整木板的 倾角平衡摩擦阻力后,挂上钩码,钩码下落,带动小车运动并打出纸带。某次实验 得到的纸带及相关数据如图乙所示。 打点计时器 小车 木板 钩码 匆 -2.56 377 单位:cm -4.00 -50.66 54.20 -57.86
10.如图所示,三个小球 A、B、C 的质量均为 m,A 与 B、C 间通过铰链用轻杆连 接,杆长为 l,B、C 置于水平地面上,用一轻质弹簧连接,弹簧处于原长。现 A 由静 止释放下降到最低点,两轻杆间夹角 α 由 60°变为 120°,A、B、C 在同一竖直 平面内运动,弹簧在弹性限度内,忽略一切摩擦,重力加速度为 g。则在此过程中 ( ) A.A 的动能达到最大前,B 受到地面的支持力小于3 2 mg B.A 的动能最大时,B 受到地面的支持力等于3 2 mg C.弹簧的弹性势能最大时,A 的加速度方向竖直向下 D.弹簧的弹性势能最大值为√3 2 mgl 答案:AB 解析:A 的动能最大时,设 B 和 C 受到地面的支持力大小均为 F,此时 A、B、C 整 体在竖直方向受力平衡,可得 2F=3mg,所以 F=3 2 mg,A 的动能达到最大前一直加 速下降,处于失重状态,所以 B 受到地面的支持力小于3 2 mg,故选项 A、B 正确;当 A 达到最低点时动能为零,此时弹簧的弹性势能最大,A 的加速度方向向上,故选 项 C 错误;A 球达到最大动能后向下做减速运动,到达最低点时三个小球的动能 均为零,由机械能守恒定律得,弹簧的弹性势能为 Ep=mg(lcos 30°-lcos 60°)= √3-1 2 mgl,故选项 D 错误。 二、实验题(共 2 小题,共 16 分) 11.(8 分)(2020·全国卷Ⅲ)某同学利用图甲所示装置验证动能定理。调整木板的 倾角平衡摩擦阻力后,挂上钩码,钩码下落,带动小车运动并打出纸带。某次实验 得到的纸带及相关数据如图乙所示。 甲 乙
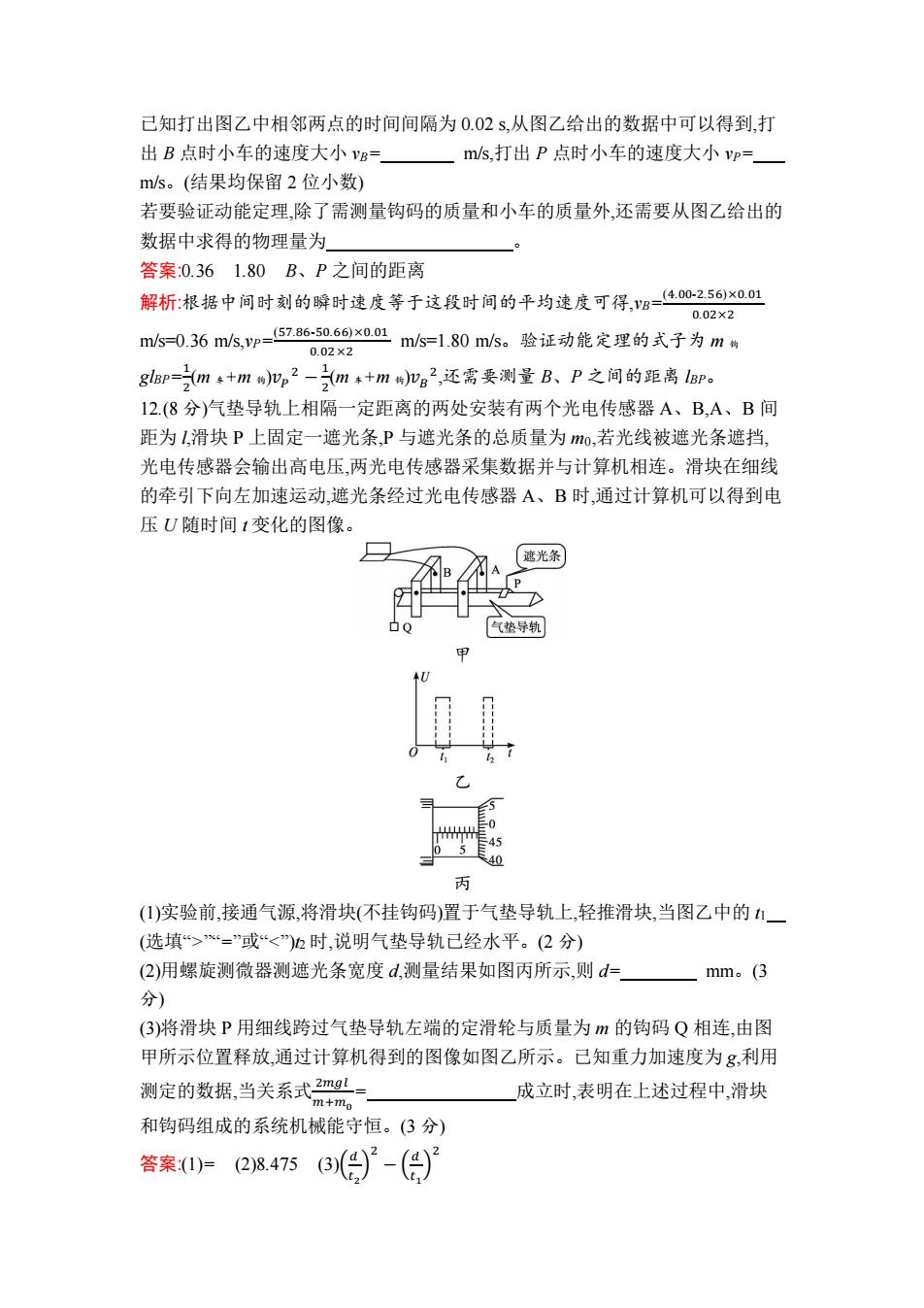
已知打出图乙中相邻两点的时间间隔为0.02s,从图乙给出的数据中可以得到,打 出B点时小车的速度大小vg=一ms,打出P点时小车的速度大小p=一 m/s。(结果均保留2位小数) 若要验证动能定理,除了需测量钩码的质量和小车的质量外,还需要从图乙给出的 数据中求得的物理量为 答案:0.361.80B、P之间的距离 解析:根据中间时刻的瞬时速度等于这段时间的平均速度可得,g-40-256x0.01 0.02×2 m5-0.36ms,p=5786-5066x001m/5-1.80m5。验证动能定理的式子为m物 0.02×2 gBP=之m季+m加,2-m+m)加g2,还需要测量B、P之间的距离1BP。 12.(8分)气垫导轨上相隔一定距离的两处安装有两个光电传感器A、B,A、B间 距为1,滑块P上固定一遮光条,P与遮光条的总质量为mo,若光线被遮光条遮挡, 光电传感器会输出高电压,两光电传感器采集数据并与计算机相连。滑块在细线 的牵引下向左加速运动,遮光条经过光电传感器A、B时,通过计算机可以得到电 压U随时间t变化的图像。 气垫导轨 45 05 40 丙 (1)实验前,接通气源,将滑块(不挂钩码)置于气垫导轨上,轻推滑块,当图乙中的1 (选填“>“=”或“<”)h时,说明气垫导轨已经水平。(2分) (2)用螺旋测微器测遮光条宽度d,测量结果如图丙所示,则d= mm。(3 分) (3)将滑块P用细线跨过气垫导轨左端的定滑轮与质量为m的钩码Q相连,由图 甲所示位置释放,通过计算机得到的图像如图乙所示。己知重力加速度为g,利用 测定的数据,当关系式2mgL m+mo 成立时,表明在上述过程中,滑块 和钩码组成的系统机械能守恒。(3分) 答案0)=284753)-(()
已知打出图乙中相邻两点的时间间隔为 0.02 s,从图乙给出的数据中可以得到,打 出 B 点时小车的速度大小 vB= m/s,打出 P 点时小车的速度大小 vP= m/s。(结果均保留 2 位小数) 若要验证动能定理,除了需测量钩码的质量和小车的质量外,还需要从图乙给出的 数据中求得的物理量为 。 答案:0.36 1.80 B、P 之间的距离 解析:根据中间时刻的瞬时速度等于这段时间的平均速度可得,vB= (4.00-2.56)×0.01 0.02×2 m/s=0.36 m/s,vP= (57.86-50.66)×0.01 0.02 ×2 m/s=1.80 m/s。验证动能定理的式子为 m 钩 glBP= 1 2 (m 车+m 钩)𝑣𝑃 2 − 1 2 (m 车+m 钩)𝑣𝐵 2 ,还需要测量 B、P 之间的距离 lBP。 12.(8 分)气垫导轨上相隔一定距离的两处安装有两个光电传感器 A、B,A、B 间 距为 l,滑块 P 上固定一遮光条,P 与遮光条的总质量为 m0,若光线被遮光条遮挡, 光电传感器会输出高电压,两光电传感器采集数据并与计算机相连。滑块在细线 的牵引下向左加速运动,遮光条经过光电传感器 A、B 时,通过计算机可以得到电 压 U 随时间 t 变化的图像。 甲 乙 丙 (1)实验前,接通气源,将滑块(不挂钩码)置于气垫导轨上,轻推滑块,当图乙中的 t1 (选填“>”“=”或“<”)t2 时,说明气垫导轨已经水平。(2 分) (2)用螺旋测微器测遮光条宽度 d,测量结果如图丙所示,则 d= mm。(3 分) (3)将滑块 P 用细线跨过气垫导轨左端的定滑轮与质量为 m 的钩码 Q 相连,由图 甲所示位置释放,通过计算机得到的图像如图乙所示。已知重力加速度为 g,利用 测定的数据,当关系式 2𝑚𝑔𝑙 𝑚+𝑚0 = 成立时,表明在上述过程中,滑块 和钩码组成的系统机械能守恒。(3 分) 答案:(1)= (2)8.475 (3)( 𝑑 𝑡2 ) 2 − ( 𝑑 𝑡1 ) 2

解析:(1)如果遮光条通过光电门的时间相等,即1=2,说明遮光条做匀速运动,即说 明气垫导轨已经水平。 (2)螺旋测微器的固定刻度读数为8mm,可动刻度读数为0.01×47.5mm=0.475 mm,所以最终读数为8mm+0.475mm=8.475mm。 (3)由于光电门的宽度很小,所以我们用很短时间内的平均速度代替瞬时速度,则 A是阳号滑块和砝码组成的系统动能的增加量△m0+mve2-vn)系统 的重力势能的减小量△正p=mgl,如果系统动能的增加量等于系统重力势能的减小 量,则系统机械能守恒,即mg-m0+me2-以2,化简得=(侣)-(月)。 m+m 三、计算题(共4小题,共44分。解答应写出必要的文字说明、方程式和重要演 算步骤,只写出最后答案不能得分,有数值计算的题,答案中必须明确写出数值和 单位) 13.(8分)假设飞机在水平跑道上的滑跑是初速度为零的匀加速直线运动,当位移 x=1.6×103m时才能达到起飞所要求的速度v=80m/s,已知飞机质量m=7.0×104 kg滑跑时受到的阻力为自身重力的。重力加速度g取10ms2,求飞机滑跑过程 中 (1)加速度a的大小: (2)牵引力的平均功率P。 答案:(1)2ms2(2)8.4×106W 解析(1)飞机滑跑过程中做初速度为零的匀加速直线运动,有v2=2ax,解得α=2 m/s2。 (2)设飞机滑跑受到的阻力为F,根据题意有F=品mg 设发动机的牵引力为F,根据牛顿第二定律有F-F=ma 设飞机滑跑过程中的平均速度为有 在滑跑阶段,牵引力的平均功率P=Fv',联立解得P=8.4×106W。 14.(10分)如图甲所示,一质量为m=1kg的物块静止在粗糙水平面上的A点,从 =0时刻开始,物块受到按如图乙所示规律变化的水平力F作用并向右运动,第3 s末物块运动到B点时速度刚好为0,第5s末物块刚好回到A点,已知物块与粗 糙水平面之间的动摩擦因数u=0.2g取10m/s2,求: ↑FN (1)A与B间的距离。 (2)水平力F在5s内对物块所做的功。 答案:(1)4m(2)24J
解析:(1)如果遮光条通过光电门的时间相等,即 t1=t2,说明遮光条做匀速运动,即说 明气垫导轨已经水平。 (2)螺旋测微器的固定刻度读数为 8 mm,可动刻度读数为 0.01×47.5 mm=0.475 mm,所以最终读数为 8 mm+0.475 mm=8.475 mm。 (3)由于光电门的宽度很小,所以我们用很短时间内的平均速度代替瞬时速度,则 vA= 𝑑 𝑡1 ,vB= 𝑑 𝑡2 ,滑块和砝码组成的系统动能的增加量 ΔEk= 1 2 (m0+m)(𝑣B 2 − 𝑣A 2 ),系统 的重力势能的减小量 ΔEp=mgl,如果系统动能的增加量等于系统重力势能的减小 量,则系统机械能守恒,即 mgl=1 2 (m0+m)(𝑣B 2 − 𝑣A 2 ),化简得 2𝑚𝑔𝑙 𝑚+𝑚0 = ( 𝑑 𝑡2 ) 2 − ( 𝑑 𝑡1 ) 2 。 三、计算题(共 4 小题,共 44 分。解答应写出必要的文字说明、方程式和重要演 算步骤,只写出最后答案不能得分,有数值计算的题,答案中必须明确写出数值和 单位) 13.(8 分)假设飞机在水平跑道上的滑跑是初速度为零的匀加速直线运动,当位移 x=1.6×103 m 时才能达到起飞所要求的速度 v=80 m/s,已知飞机质量 m=7.0×104 kg,滑跑时受到的阻力为自身重力的 1 10 ,重力加速度 g 取 10 m/s2 ,求飞机滑跑过程 中 (1)加速度 a 的大小; (2)牵引力的平均功率 P。 答案:(1)2 m/s2 (2)8.4×106 W 解析:(1)飞机滑跑过程中做初速度为零的匀加速直线运动,有 v 2=2ax,解得 a=2 m/s2。 (2)设飞机滑跑受到的阻力为 F 阻,根据题意有 F 阻= 1 10 mg 设发动机的牵引力为 F,根据牛顿第二定律有 F-F 阻=ma 设飞机滑跑过程中的平均速度为 v',有 v'=𝑣 2 在滑跑阶段,牵引力的平均功率 P=Fv',联立解得 P=8.4×106 W。 14.(10 分)如图甲所示,一质量为 m=1 kg 的物块静止在粗糙水平面上的 A 点,从 t=0 时刻开始,物块受到按如图乙所示规律变化的水平力 F 作用并向右运动,第 3 s 末物块运动到 B 点时速度刚好为 0,第 5 s 末物块刚好回到 A 点,已知物块与粗 糙水平面之间的动摩擦因数 μ=0.2,g 取 10 m/s2 ,求: (1)A 与 B 间的距离。 (2)水平力 F 在 5 s 内对物块所做的功。 答案:(1)4 m (2)24 J

解析:(1)根据题目条件及题图乙可知,物块在从B返回A的过程中,在恒力作用下 做匀加速直线运动,即 F-umg=ma 由运动学公式知,xu 代入数据解得xAB=4m。 (2)物块在前3s内动能改变量为零,由动能定理得 W-W=0,即W1-mng XAB=0 则前3s内水平力F做的功为W1=8J 根据W=F1得,水平力F在第3~5s时间内所做的功为W2=Fx4B=16J 则水平力F在5S内对物块所做的功为 W=W1+W2=24J。 15.(12分)如图所示,半径R=0.5m的光滑半圆形轨道固定在竖直平面内,半圆形 轨道与光滑水平地面相切于轨道最低端点A。质量m=1kg的小球以初速度 o=5s从A点冲上竖直半圆轨道,沿轨道运动到B点飞出,最后落在水平地面上 的C点g取10m/s2,不计空气阻力。 (I)求小球运动到轨道末端B点时的速度vB。 (2)求A、C两点间的距离x。 (3)若小球以不同的初速度冲上竖直半圆轨道,并沿轨道运动到B点飞出,落在水 平地面上。求小球落点与A点间的最小距离xmin 答案:(1)vW5m/s(2)1m(3)1m 解析()由机械能守恒定律得号mv,2=专mvg2+mg2R 解得vB=V5m/s。 2)由平抛运动规律得2R=3P,x=v8l 解得x=1m。 (3)设小球运动到B点,半圆轨道对小球的压力为FN 圆周运动向心力N+mg=m2 R 当F=0时,小球运动到轨道末端B点时的速度最小,VEmin=V5m/s 由(2)的计算可知,最小距离xmin=x=1m。 16.(14分)如图所示,水平轨道AB和DE分别长2.0m和10.0m,光滑圆弧形轨道 CD半径R=0.5m,光滑斜面EF足够长。一质量m=0.4kg的滑块(可视为质点)静 止于水平轨道上的A点,现对滑块施加一水平外力,使其向右运动,外力的功率恒 为P=10.0W;经过一段时间后撤去外力,滑块继续滑行至B点后水平飞出,恰好在 C点沿切线方向进入固定在竖直平面内的光滑圆弧形轨道CD,轨道的最低点D
解析:(1)根据题目条件及题图乙可知,物块在从 B 返回 A 的过程中,在恒力作用下 做匀加速直线运动,即 F-μmg=ma 由运动学公式知,xAB= 1 2 at2 代入数据解得 xAB=4 m。 (2)物块在前 3 s 内动能改变量为零,由动能定理得 W1-Wf=0,即 W1-μmg·xAB=0 则前 3 s 内水平力 F 做的功为 W1=8 J 根据 W=Fl 得,水平力 F 在第 3~5 s 时间内所做的功为 W2=F·xAB=16 J 则水平力 F 在 5 s 内对物块所做的功为 W=W1+W2=24 J。 15.(12 分)如图所示,半径 R=0.5 m 的光滑半圆形轨道固定在竖直平面内,半圆形 轨道与光滑水平地面相切于轨道最低端点 A。质量 m=1 kg 的小球以初速度 v0=5 m/s 从 A 点冲上竖直半圆轨道,沿轨道运动到 B 点飞出,最后落在水平地面上 的 C 点,g 取 10 m/s2 ,不计空气阻力。 (1)求小球运动到轨道末端 B 点时的速度 vB。 (2)求 A、C 两点间的距离 x。 (3)若小球以不同的初速度冲上竖直半圆轨道,并沿轨道运动到 B 点飞出,落在水 平地面上。求小球落点与 A 点间的最小距离 xmin。 答案:(1)√5 m/s (2)1 m (3)1 m 解析:(1)由机械能守恒定律得1 2 𝑚𝑣0 2 = 1 2 𝑚𝑣𝐵 2+mg·2R 解得 vB=√5 m/s。 (2)由平抛运动规律得 2R=1 2 gt2 ,x=vBt 解得 x=1 m。 (3)设小球运动到 B 点,半圆轨道对小球的压力为 FN 圆周运动向心力 FN+mg=𝑚𝑣𝐵 2 𝑅 当 FN=0 时,小球运动到轨道末端 B 点时的速度最小,vBmin=√5 m/s 由(2)的计算可知,最小距离 xmin=x=1 m。 16.(14 分)如图所示,水平轨道 AB 和 DE 分别长 2.0 m 和 10.0 m,光滑圆弧形轨道 CD 半径 R=0.5 m,光滑斜面 EF 足够长。一质量 m=0.4 kg 的滑块(可视为质点)静 止于水平轨道上的 A 点,现对滑块施加一水平外力,使其向右运动,外力的功率恒 为 P=10.0 W;经过一段时间后撤去外力,滑块继续滑行至 B 点后水平飞出,恰好在 C 点沿切线方向进入固定在竖直平面内的光滑圆弧形轨道 CD,轨道的最低点 D

处装有压力传感器,当滑块到达传感器上方时,传感器的示数为25.6N;已知半径 OC和竖直方向的夹角a=37°,滑块与水平轨道AB、DE间的动摩擦因数均为 4=0.1,空气阻力可忽略,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8。求: B 0 A-1.R D (I)滑块运动到C点时速度vc的大小(4分) (2)滑块从B点运动到C点重力做的功:(5分) (3)滑块在水平轨道AB段上时,水平外力作用在滑块上的时间1和滑块最终停在 距D点多远的位置。(5分) 答案:(1)5m/s(2)1.8J(3)0.4s距D点6.5m的位置上 解析(1)滑块运动到D点时,由牛顿第二定律得FN-mg=mD R 滑块由C点运动到D点的过程」 由机械能守恒定律得mgR(1-cos)+2mv2=mvn2 联立解得vc=5m/s。 (2)滑块运动到B,点时的速度为vB=vccos a=4ms 滑块由B点运动到C点的过程,由动能定理得%m"。2-m2 代入数据解得WG=1.8J。 (3)滑块由A点运动到B,点的过程,由动能定理得Pt-mgl=三mvg2 解得t=0.4s 滑块由D点运动到停止的过程,由动能定理得umg=0mv2 解得x=13.5m 水平轨道DE长10.0m,滑块冲上斜面EF后返回DE,△x=10m-(13.5-10)m=6.5m 所以滑块最终停在距D点6.5m的位置上
处装有压力传感器,当滑块到达传感器上方时,传感器的示数为 25.6 N;已知半径 OC 和竖直方向的夹角 α=37°,滑块与水平轨道 AB、DE 间的动摩擦因数均为 μ=0.1,空气阻力可忽略,重力加速度 g 取 10 m/s2 ,sin 37°=0.6,cos 37°=0.8。求: (1)滑块运动到 C 点时速度 vC的大小;(4 分) (2)滑块从 B 点运动到 C 点重力做的功;(5 分) (3)滑块在水平轨道 AB 段上时,水平外力作用在滑块上的时间 t 和滑块最终停在 距 D 点多远的位置。(5 分) 答案:(1)5 m/s (2)1.8 J (3)0.4 s 距 D 点 6.5 m 的位置上 解析:(1)滑块运动到 D 点时,由牛顿第二定律得 FN-mg= 𝑚𝑣𝐷 2 𝑅 滑块由 C 点运动到 D 点的过程, 由机械能守恒定律得 mgR(1-cos α)+ 1 2 𝑚𝑣𝐶 2 = 1 2 𝑚𝑣𝐷 2 联立解得 vC=5 m/s。 (2)滑块运动到 B 点时的速度为 vB=vCcos α=4 m/s 滑块由 B 点运动到 C 点的过程,由动能定理得 WG= 1 2 𝑚𝑣𝐶 2 − 1 2 𝑚𝑣𝐵 2 代入数据解得 WG=1.8 J。 (3)滑块由 A 点运动到 B 点的过程,由动能定理得 Pt-μmgl=1 2 𝑚𝑣𝐵 2 解得 t=0.4 s 滑块由 D 点运动到停止的过程,由动能定理得-μmgx=0- 1 2 𝑚𝑣𝐷 2 解得 x=13.5 m 水平轨道 DE 长 10.0 m,滑块冲上斜面 EF 后返回 DE,Δx=10 m-(13.5-10) m=6.5 m 所以滑块最终停在距 D 点 6.5 m 的位置上