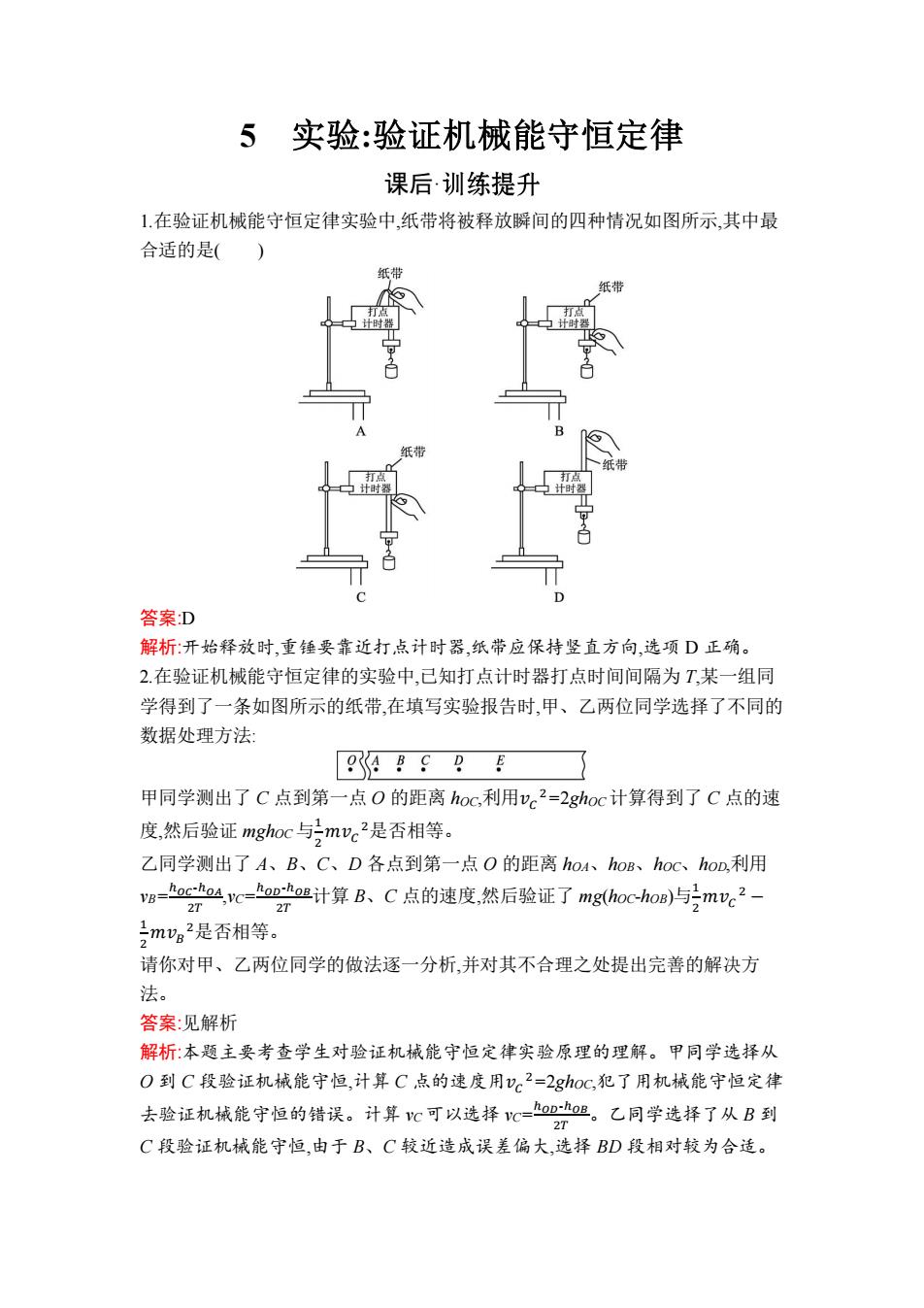
5实验:验证机械能守恒定律 课后·训练提升 1.在验证机械能守恒定律实验中,纸带将被释放瞬间的四种情况如图所示,其中最 合适的是( ) 纸带 D 答案D 解析:开始释放时,重锤要靠近打点计时器,纸带应保持竖直方向,选项D正确。 2.在验证机械能守恒定律的实验中,已知打点计时器打点时间间隔为T,某一组同 学得到了一条如图所示的纸带,在填写实验报告时,甲、乙两位同学选择了不同的 数据处理方法: 94 B C B E 甲同学测出了C点到第一点O的距离hoc,利用vc2=2ghoc计算得到了C点的速 度,然后验证mghoc-与号mve2是否相等。 乙同学测出了A、B、C、D各点到第一点O的距离hoA、hoB、hoc、hop,利用 vg=oco4vc=opo计算B、C点的速度,然后验证了mg(hoc--hoB)与mue2- 27 2T m。是否相等。 请你对甲、乙两位同学的做法逐一分析,并对其不合理之处提出完善的解决方 法。 答案:见解析 解析:本题主要考查学生对验证机械能守恒定律实验原理的理解。甲同学选择从 O到C段验证机械能守恒,计算C点的速度用v2=2ghoC,犯了用机械能守恒定律 去验证机械能守恒的错误。计算C可以选择C=Dh胆。乙同学选择了从B到 2T C段验证机械能守恒,由于B、C较近造成误差偏大,选择BD段相对较为合适
5 实验:验证机械能守恒定律 课后· 1.在验证机械能守恒定律实验中,纸带将被释放瞬间的四种情况如图所示,其中最 合适的是( ) 答案:D 解析:开始释放时,重锤要靠近打点计时器,纸带应保持竖直方向,选项 D 正确。 2.在验证机械能守恒定律的实验中,已知打点计时器打点时间间隔为 T,某一组同 学得到了一条如图所示的纸带,在填写实验报告时,甲、乙两位同学选择了不同的 数据处理方法: 甲同学测出了 C 点到第一点 O 的距离 hOC,利用𝑣𝐶 2=2ghOC 计算得到了 C 点的速 度,然后验证 mghOC 与 1 2 𝑚𝑣𝐶 2是否相等。 乙同学测出了 A、B、C、D 各点到第一点 O 的距离 hOA、hOB、hOC、hOD,利用 vB= ℎ𝑂𝐶-ℎ𝑂𝐴 2𝑇 ,vC= ℎ𝑂𝐷-ℎ𝑂𝐵 2𝑇 计算 B、C 点的速度,然后验证了 mg(hOC-hOB)与 1 2 𝑚𝑣𝐶 2 − 1 2 𝑚𝑣𝐵 2是否相等。 请你对甲、乙两位同学的做法逐一分析,并对其不合理之处提出完善的解决方 法。 答案:见解析 解析:本题主要考查学生对验证机械能守恒定律实验原理的理解。甲同学选择从 O 到 C 段验证机械能守恒,计算 C 点的速度用𝑣𝐶 2=2ghOC,犯了用机械能守恒定律 去验证机械能守恒的错误。计算 vC可以选择 vC= ℎ𝑂𝐷-ℎ𝑂𝐵 2𝑇 。乙同学选择了从 B 到 C 段验证机械能守恒,由于 B、C 较近造成误差偏大,选择 BD 段相对较为合适

3.某同学设计出如图所示验证机械能守恒定律的实验装置,小球用轻质细绳悬挂 于O点,在O点正下方固定一刀片,并在水平地面上用重锤记录下O点在水平面 的投影,将小球拉至与O等高的水平位置处,绳被拉直,从静止释放小球,当小球到 达O点正下方时,刀片割断细绳,小球做平抛运动,记录下小球的落点。 10 刀片 (1)下列物理量中需要测量的是 (填选项前的字母)。 A.细绳的长度1 B.O点到地面的高度h C.O点在地面的投影到小球落点的水平距离x D.小球的质量m (2)利用题(1)中的字母,需要验证的等式是 答案:(1)ABC(2)x2=41h-) 2 解析:若小球运动过程中机械能守恒,则有mgh=mgh-+m 2(h-i) 化简得 x2=4(h-),由此式可知,要测量的有细绳的长度1、O点到地面的高度h、O点在 地面的投影到小球落点的水平距离x,而小球的质量不需要测量,A、B、C正确。 4.某同学用如图甲所示的实验装置验证机械能守恒定律,通过实验数据分析,发现 本实验存在较大的误差。为此改用如图乙所示的实验装置:通过电磁铁控制的小 铁球从A点自由下落,下落过程中经过光电门B时,通过与之相连的毫秒计时器 (图中未画出)记录挡光时间1,用毫米刻度尺测出AB之间的距离h,用游标卡尺测 得小铁球的直径d(dk),重力加速度为g。则小铁球经过光电门时的瞬时速度 V= 。 如果d、th、g满足关系式P= 就可验证机械能守恒定 律。比较两个方案,改进后的方案相比原方案最主要的优点是 打点 -纸带 计时器 接电源夹子 白一陆码
3.某同学设计出如图所示验证机械能守恒定律的实验装置,小球用轻质细绳悬挂 于 O 点,在 O 点正下方固定一刀片,并在水平地面上用重锤记录下 O 点在水平面 的投影,将小球拉至与 O 等高的水平位置处,绳被拉直,从静止释放小球,当小球到 达 O 点正下方时,刀片割断细绳,小球做平抛运动,记录下小球的落点。 (1)下列物理量中需要测量的是 (填选项前的字母)。 A.细绳的长度 l B.O 点到地面的高度 h C.O 点在地面的投影到小球落点的水平距离 x D.小球的质量 m (2)利用题(1)中的字母,需要验证的等式是 。 答案:(1)ABC (2)x 2=4l(h-l) 解析:若小球运动过程中机械能守恒,则有 mgh=mg(h-l)+ 1 2 𝑚 ( 𝑥 √ 2(ℎ-𝑙) 𝑔 ) 2 ,化简得 x 2=4l(h-l),由此式可知,要测量的有细绳的长度 l、O 点到地面的高度 h、O 点在 地面的投影到小球落点的水平距离 x,而小球的质量不需要测量,A、B、C 正确。 4.某同学用如图甲所示的实验装置验证机械能守恒定律,通过实验数据分析,发现 本实验存在较大的误差。为此改用如图乙所示的实验装置:通过电磁铁控制的小 铁球从 A 点自由下落,下落过程中经过光电门 B 时,通过与之相连的毫秒计时器 (图中未画出)记录挡光时间 t,用毫米刻度尺测出 AB 之间的距离 h,用游标卡尺测 得小铁球的直径 d(d<h),重力加速度为 g。则小铁球经过光电门时的瞬时速度 v= 。如果 d、t、h、g 满足关系式 t 2= ,就可验证机械能守恒定 律。比较两个方案,改进后的方案相比原方案最主要的优点是 。 甲

答案号云消除了纸带与打点计时器之间的阻力的影响 解析:匀变速直线运动中中间时刻的瞬时速度等于该过程中的平均速度,由此可以 求小铁球经过光电门时的瞬时建度号由运功学公式2-2gh得F器比较两 个方案,改进后的方案相比原方案最主要的优点是消除了纸带与打点计时器之间 的阻力的影响。 5.验证机械能守恒定律的实验采用重锤自由下落的方法。(g取10m/s2) (1)用公式mm2=mgh时,对纸带上起点的要求是初速度为为达到此目的,所 选择的纸带第一、第二两点间距应接近 (2)若实验中所用重锤的质量m=1kg,打点纸带如甲图所示,打点时间间隔为0.02 S,则记录B点时,重锤速度vB= 重锤的动能EkB= 从开始下 落起至B点,重锤的重力势能减少量是 因此可得出的结论 是 31.4 品 单位:mm 甲 (3)根据纸带算出的相关各点的速度值,量出下落的距离,则以号为纵轴,以h为横 轴画出的图线应是乙图中的 答案:(1)02mm (2)0.59/s0.174J0.176J在实验误差允许的范围内,重锤动能的增加量等 于重力势能的减少量 (3)C 解析:(1)初速度为0,所选第一、第二两点接近2mm。 (2)yB=4c=3147.8)x103 m/s=0.59m/s 2T 2×0.02 EkB=2mwg2=3×1×0.592J=0.174J
乙 答案: 𝑑 𝑡 𝑑 2 2𝑔ℎ 消除了纸带与打点计时器之间的阻力的影响 解析:匀变速直线运动中中间时刻的瞬时速度等于该过程中的平均速度,由此可以 求小铁球经过光电门时的瞬时速度 v= 𝑑 𝑡 ,由运动学公式 v 2=2gh 得 t 2= 𝑑 2 2𝑔ℎ ;比较两 个方案,改进后的方案相比原方案最主要的优点是消除了纸带与打点计时器之间 的阻力的影响。 5.验证机械能守恒定律的实验采用重锤自由下落的方法。(g 取 10 m/s2 ) (1)用公式1 2 mv2=mgh 时,对纸带上起点的要求是初速度为 ,为达到此目的,所 选择的纸带第一、第二两点间距应接近 。 (2)若实验中所用重锤的质量 m=1 kg,打点纸带如甲图所示,打点时间间隔为 0.02 s,则记录 B 点时,重锤速度 vB= ,重锤的动能 EkB= ,从开始下 落起至 B 点,重锤的重力势能减少量是 ,因此可得出的结论 是 。 甲 (3)根据纸带算出的相关各点的速度值,量出下落的距离,则以𝑣 2 2 为纵轴,以 h 为横 轴画出的图线应是乙图中的 。 乙 答案:(1)0 2 mm (2)0.59 m/s 0.174 J 0.176 J 在实验误差允许的范围内,重锤动能的增加量等 于重力势能的减少量 (3)C 解析:(1)初速度为 0,所选第一、第二两点接近 2 mm。 (2)vB= 𝑥𝐴𝐶 2𝑇 = (31.4-7.8)×10 -3 2×0.02 m/s=0.59 m/s EkB= 1 2 𝑚𝑣𝐵 2 = 1 2 ×1×0.592 J=0.174 J

△Ep=mghB=1×10×17.6×10-3J=0.176J. (3)由22=mgh可得三=ghch,C正确。 6.下图为验证小球做自由落体运动时机械能守恒的装置图。图中O点为释放小 球的初始位置,A、B、C、D各点为固定速度传感器的位置,A、B、C、D、O各 点在同一竖直线上。 D (1)已知当地的重力加速度为g,则要完成实验,还需要测量的物理量是 A.小球的质量m B.小球下落到每一个速度传感器时的速度ⅴ C.各速度传感器与O点之间的竖直距离h D.小球自初始位置至下落到每一个速度传感器时所用的时间1 (2)作出2-h图像,由图像算出其斜率k,当k=时,可以认为小球在下落过程 中系统机械能守恒。 答案:(1)BC(2)2g 解析:()小球做自由落体运动时,由机械能守恒定律得mgh=m2,即gh=二2,故需 要测量小球下落到每一个速度传感器时的速度ⅴ和高度h,不需要测量小球的质 量m和下落时间1,故选项B、C正确,A、D错误。 (2)若机械能守恒,则mgh=之m2 得v2=2gh 则2-h图像的斜率k=2g,即可验证机械能守恒。 7.“阿特伍德机”是早期英国数学家和物理学家阿特伍德创制的一种著名的力学 实验装置,用来研究匀变速直线运动的规律。某同学对阿特伍德机”模型加以改 进后用来验证机械能守恒定律,如图所示。(已知重力加速度为g) 光电门 B c 光A (1)实验时,该同学进行了如下操作 ①将质量均为m的重物A、B(A含挡光片、B含挂钩)用绳连接后,跨放在定滑轮 上,处于静止状态。测量出 (选填“A的上表面“A的下表面”或 “挡光片中心)到光电门中心的竖直距离h
ΔEp=mghB=1×10×17.6×10-3 J=0.176 J。 (3)由 1 2 mv2=mgh 可得𝑣 2 2 =gh∝h,C 正确。 6.下图为验证小球做自由落体运动时机械能守恒的装置图。图中 O 点为释放小 球的初始位置,A、B、C、D 各点为固定速度传感器的位置,A、B、C、D、O 各 点在同一竖直线上。 (1)已知当地的重力加速度为 g,则要完成实验,还需要测量的物理量是 ; A.小球的质量 m B.小球下落到每一个速度传感器时的速度 v C.各速度传感器与 O 点之间的竖直距离 h D.小球自初始位置至下落到每一个速度传感器时所用的时间 t (2)作出 v 2 -h 图像,由图像算出其斜率 k,当 k= 时,可以认为小球在下落过程 中系统机械能守恒。 答案:(1)BC (2)2g 解析:(1)小球做自由落体运动时,由机械能守恒定律得 mgh=1 2 mv2 ,即 gh=1 2 v 2 ,故需 要测量小球下落到每一个速度传感器时的速度 v 和高度 h,不需要测量小球的质 量 m 和下落时间 t,故选项 B、C 正确,A、D 错误。 (2)若机械能守恒,则 mgh=1 2 mv2 得 v 2=2gh 则 v 2 -h 图像的斜率 k=2g,即可验证机械能守恒。 7.“阿特伍德机”是早期英国数学家和物理学家阿特伍德创制的一种著名的力学 实验装置,用来研究匀变速直线运动的规律。某同学对“阿特伍德机”模型加以改 进后用来验证机械能守恒定律,如图所示。(已知重力加速度为 g) (1)实验时,该同学进行了如下操作: ①将质量均为 m'的重物 A、B(A 含挡光片、B 含挂钩)用绳连接后,跨放在定滑轮 上,处于静止状态。测量出 (选填“A 的上表面”“A 的下表面”或 “挡光片中心”)到光电门中心的竖直距离 h

②在B的下端挂上质量为m的物块C,让系统(重物A、B以及物块C)中的物体 由静止开始运动,光电门记录挡光片挡光的时间为△1。 ③测出挡光片的宽度d,计算有关物理量,验证机械能守恒定律。 (2)如果系统(重物A、B以及物块C)的机械能守恒,应满足的关系式 为 (3)引起该实验系统误差的主要原因有 。 (写一条 即可) (4)验证实验结束后,该同学突发奇想:如果系统(重物A、B以及物块C)的机械能 守恒,不断增大物块C的质量m,重物B的加速度a也将不断增大,那么a与m之 间有怎样的定量关系?a随m增大会趋于一个什么值?请你帮该同学解决下列问 题 ①写出a与m之间的关系式: ②最终a的值会趋于 答案:(1)①挡光片中心 (2mgh-(2m'+m (3)绳子有一定的质量(或滑轮与轴之间有摩擦、重物运动受到空气阻力等) (4)①a=mg②重力加速度g 2m'+m 解析2)A经过光电门时,系统的速度大小为v是如果系统(重物A、B以及物块 C)的机械能守恒,应满足的关系式为mgh-m+2mw2-m+2m9侣)》。 (3)引起该实验系统误差的主要原因是绳子有一定的质量、滑轮与轴之间有摩 擦、重物运动受到空气阻力等。 (④0对系统交力分析,根据牛顿第二定律可得mg=(m+2ma,解得amm3。 ②由am2m3可知,当不断增大物块C的质量m时,最终a的值会楚于重 1 力加速度g
②在 B 的下端挂上质量为 m 的物块 C,让系统(重物 A、B 以及物块 C)中的物体 由静止开始运动,光电门记录挡光片挡光的时间为 Δt。 ③测出挡光片的宽度 d,计算有关物理量,验证机械能守恒定律。 (2)如果系统(重物 A、B 以及物块 C)的机械能守恒,应满足的关系式 为 。 (3)引起该实验系统误差的主要原因有 。(写一条 即可) (4)验证实验结束后,该同学突发奇想:如果系统(重物 A、B 以及物块 C)的机械能 守恒,不断增大物块 C 的质量 m,重物 B 的加速度 a 也将不断增大,那么 a 与 m 之 间有怎样的定量关系?a 随 m 增大会趋于一个什么值?请你帮该同学解决下列问 题: ①写出 a 与 m 之间的关系式: 。 ②最终 a 的值会趋于 。 答案:(1)①挡光片中心 (2)mgh=1 2 (2m'+m)( 𝑑 Δ𝑡 ) 2 (3)绳子有一定的质量(或滑轮与轴之间有摩擦、重物运动受到空气阻力等) (4)①a= 𝑚𝑔 2𝑚'+𝑚 ②重力加速度 g 解析:(2)A 经过光电门时,系统的速度大小为 v= 𝑑 Δ𝑡 ,如果系统(重物 A、B 以及物块 C)的机械能守恒,应满足的关系式为 mgh=1 2 (m+2m')v 2= 1 2 (m+2m')( 𝑑 Δ𝑡 ) 2 。 (3)引起该实验系统误差的主要原因是绳子有一定的质量、滑轮与轴之间有摩 擦、重物运动受到空气阻力等。 (4)①对系统受力分析,根据牛顿第二定律可得 mg=(m+2m')a,解得 a= 𝑚 𝑚+2𝑚' g。 ②由 a= 𝑚 𝑚+2𝑚' g= 1 1+ 2𝑚' 𝑚 g 可知,当不断增大物块 C 的质量 m 时,最终 a 的值会趋于重 力加速度 g