
上游充通大¥ e SHANGHAI JIAO TONG UNIVERSITY Chapter 7.Solution Review Solutions Thermodynamic activity Partial molar quantities Relative partial molar quantities Entropy of mixing:ideal solution Enthalpy of mixing:ideal solution Graphical representation etc
Review Solutions Thermodynamic activity Partial molar quantities Relative partial molar quantities Entropy of mixing: ideal solution Enthalpy of mixing: ideal solution Graphical representation etc. Chapter 7. Solution

上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY Nomenclature Solutions:溶液 Chemical potential:化学位(势) Thermodynamic activity:热力学活度 Ideal solution:理想溶液 Relative partial molar quantities:相对偏摩尔量 Entropy of mixing:混合嫡 Graphical representation of partial molar quantities: 偏摩尔量的图示
Nomenclature

上游充通大¥ Introduction SHANGHAI JIAO TONG UNIVERSITY Chemical changes among pure components and compounds Solutions:elements or compounds dissolved in one another Many of the interesting properties of materials and many important chemical reactions take place Thermodynamics of these solutions We are trying to understand the energy of the changes in solution chemical reaction,phase transformation
Introduction We are trying to understand the energy of the changes in solution chemical reaction, phase transformation

上游充通大¥ Introduction SHANGHAI JIAO TONG UNIVERSITY 相变是物质由一个相向另一个相的传递过程 扩散是物质由高浓度区向低浓度区的传递过程 化学反应可以看作是物质由反应物向产物的传递过程 在传递过程中化学势将起决定作用。 在恒温恒压下, dG=∑4dn, 再由自由能判据dG≤0可得判据的另一形式(化学势判据): ∑4dn,≤0 在相变过程中物质总是由化学势高的一相向转向化学势低的 一相,直到两相中的化学势相等为止。而物质在两相中存在的 化学势差△μ;是物质传递的动力
Introduction

上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY 7.1 Thermodynamic activity Fugacity is defined for gases: dG;=RTd(In fi) Energetic,in terms of energy or chemical potential Thermodynamic activity of a component,i,is defined as: C;≡ The fugacity of the component iin its standard state. The fugacity of a condensed phase is equal to the fugacity of the vapor phase in equilibrium with it. The fugacity of the vapor is equal to the pressure of the vapor,if the vapor in equilibrium with the condensed phase is ideal
7.1 Thermodynamic activity Energetic, in terms of energy or chemical potential

上游充通大粤 SHANGHAI JIAO TONG UNIVERSITY 7.1 Thermodynamic activity (2) Standard state not reference state In liquid solutions and solid solutions the pure materials at one atmosphere pressure and specified crystal structure. Solid solution of iron and nickel The pure iron (bec or fec)and pure nickel are chosen as the standard state. G:-Gjpure =G1-G;=RTInar dGi =RTd(Infi) Relationship between energy and the concentration Ideal solution:(definition) The fugacity of component i is equal to the mole fraction of component i multiplied by the fugacity of i in the pure state. Temperature is not part of the definition of a standard state
7.1 Thermodynamic activity (2) Temperature is not part of the definition of a standard state Relationship between energy and the concentration (definition)

上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY 7.1 Thermodynamic activity (3) Pure state as standard state fi=fp xifp fi=xif f i(ideal solution) G:-Gipue =G:-G=RTIna;-RTInx
7.1 Thermodynamic activity (3) = RTlnxi

上游充通大粤 SHANGHAI JIAO TONG UNIVERSITY 7.1 Thermodynamic activity (4) The change of Gibbs free energy upon mixing: i-RTh solution)) f Ji(pure) f =f” Grd=Gi(sohmam)-G(pue)=RTInx (ideal solution) 0;=i
7.1 Thermodynamic activity (4)
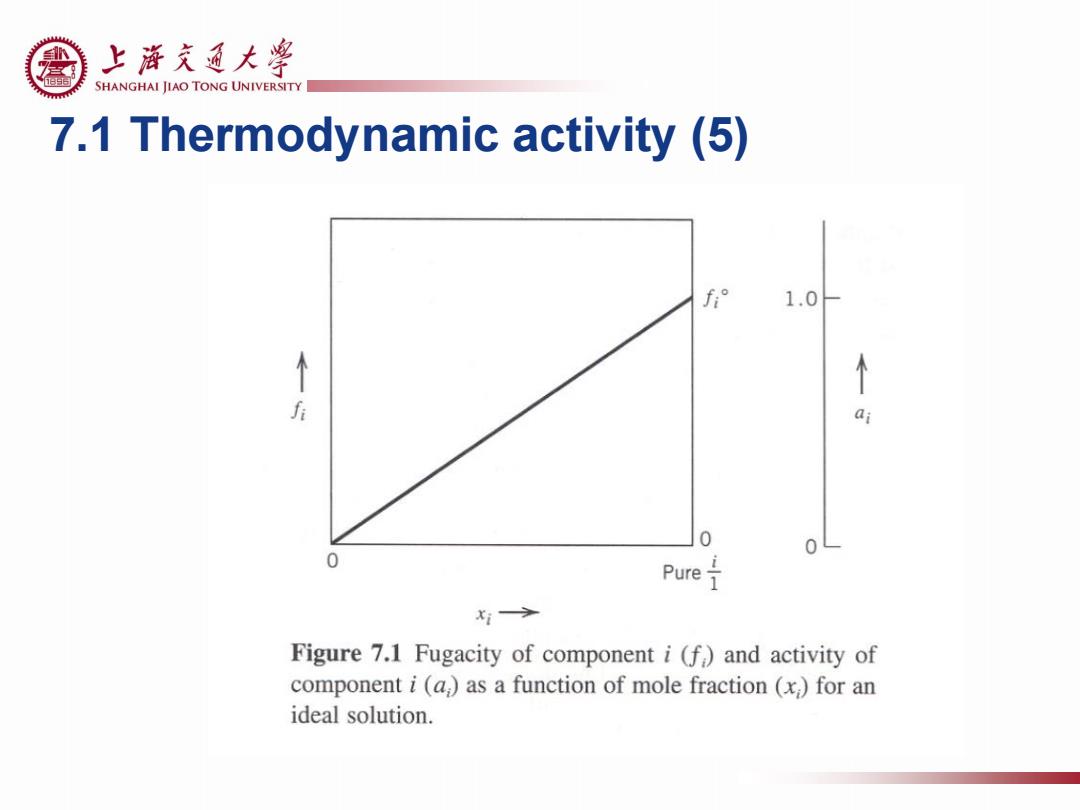
上游充通大粤 e SHANGHAI JIAO TONG UNIVERSITY 7.1 Thermodynamic activity (5) f° 1.0 0 0 Pure x1> Figure 7.1 Fugacity of component i(f)and activity of component i(a,)as a function of mole fraction (x,)for an ideal solution
7.1 Thermodynamic activity (5)

上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY 7.2 Partial Molar Quantities (1) The properties of a material in solution are represented by the partial molar quantities..偏摩尔量 The volume of the solution consisting of materials A and B,at constant temperature and pressure,is the function of the amount of A and the amount of B V =V(nA,nB)T.P Volume is a point or state function dV av dnB OnA)T.P.nB
7.2 Partial Molar Quantities (1) The properties of a material in solution are represented by the partial molar quantities. 偏摩尔量