
上游充通大 SHANGHAI JIAO TONG UNIVERSITY Chapter 10.Statistical Thermodynamics 1.Macrosates and Microstates宏观状态与微观状态 2.微观状态数与最可几分布 3. Boltzmann假定与配置熵 4.理想固溶体熵 5.第三定律 6.Gibbs公式 7.Boltzmann分布* 8.配分函数* 9.Fermi-Dirac分布* IAO TONG UNI David V.Ragone,Thermodynamics of Materials,John Wiley Sons,Inc.,1995,Vol.I,Chap 10 &Vol.II,Chap 2.. 江伯鸿,材料热力学,上海交通大学出版社,1999,第八章 徐祖耀,李麟,材料热力学,科学出版社,2000,第九第十章
Chapter 10. Statistical Thermodynamics 1. Macrosates and Microstates宏观状态与微观状态 2. 微观状态数与最可几分布 3. Boltzmann假定与配置熵 4. 理想固溶体熵 5. 第三定律 6. Gibbs 公式 7. Boltzmann 分布* 8. 配分函数* 9. Fermi-Dirac 分布*

上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY Macroscopic thermodynamics microscopic thermodynamics/statistical thermodynamics Root-mean-square average rate of motion Macrosate/Microstate:宏观态/微观态 The time average of the properties of a system is equivalent to the instantaneous average over the ensemble of the microstates available to the system. Ensemble:系综 Microcanonical/canonical/macrocanonical::微/正则/巨 Degeneracy:简并度 Partition function:配分函数

上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY Macroscopic thermodynamics Microscopic thermodynamcis 宏观世界 统计热力学 微观世界 (热力学) (量子力学) Statistical averaging Temperature,pressure,heat etc. Molecular motion,structures, No information about atomic vibrations. structures and quantum mechanics AO TONG U! Depend heavily on the quantum mechanics Constant P,T for a system at equilibrium Atoms or molecules are in motion,and their configurations are changing constantly
Macroscopic thermodynamics Microscopic thermodynamcis Temperature, pressure, heat etc. No information about atomic structures and quantum mechanics Molecular motion, structures, vibrations. Depend heavily on the quantum mechanics Statistical averaging Constant P, T for a system at equilibrium Atoms or molecules are in motion, and their configurations are changing constantly
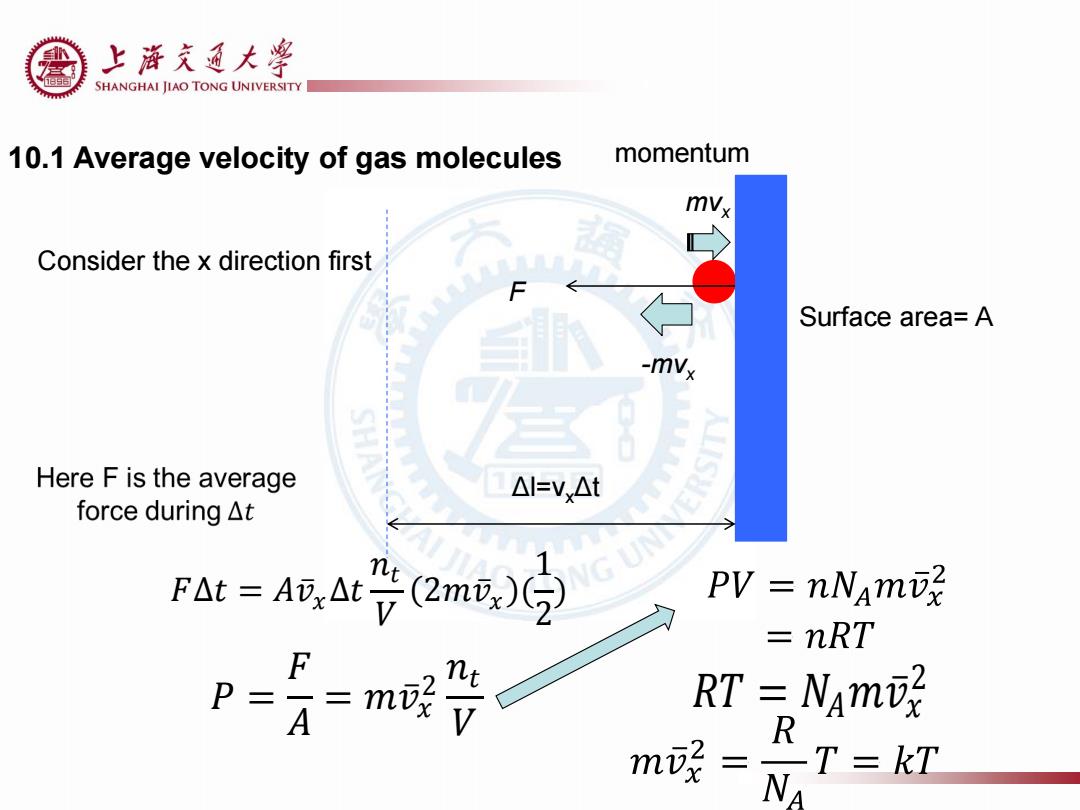
上浒充通大率 SHANGHAI JIAO TONG UNIVERSITY 10.1 Average velocity of gas molecules momentum mvx Consider the x direction first Surface area=A -mv Here F is the average △I=Vx△t force during△t Fat=A,At号(2m或)9 PV =nNami =nRT P m晚 RT NAm m晚= T=7 R
10.1 Average velocity of gas molecules mvx -mvx 𝐹∆𝑡 = 𝐴𝑣 𝑥∆𝑡 𝑛𝑡 𝑉 2𝑚𝑣 𝑥 ( 1 2 ) F Δl=vxΔt Surface area= A 𝑃 = 𝐹 𝐴 = 𝑚𝑣 𝑥 2 𝑛𝑡 𝑉 𝑅𝑇 = 𝑁𝐴𝑚𝑣 𝑥 2 momentum Consider the x direction first

上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY 2=呢十好+昭 2=3晚 1 mv2 kT 3 AIJIAO TONG UNI 1 3 (E〉= m2 2 二 2 kT

上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY Average Velocity of Gas Molecules Monatomic,ideal gas in equilibrium with its pressure and temperature 1-2 my=kT PV=nRT 3 The average energy,,of the molecule is 2 3 Specific Internal Energy per mole: R 2 U=N U=N 3 kT= 32 RT C-( 3-2 R
v kT 2 m 3 1 The average energy, , of the molecule is kT 2 3 m 2 1 2 v R 2 3 ) T U ( RT 2 3 kT 2 3 U U V A A C N N E Specific Internal Energy per mole:

上浒充通大警 SHANGHAI JIAO TONG UNIVERSITY Average Velocity of Gas Molecules The rate of motion of molecules in O2 at macroscopic equilibrium 2=3kT/m=23.4×104m2/S2 v=483m/S NAIIAO TONG UNIV R=8.314472(15)JK-1mo-1 K=R/NA=1.38X10-23 m=32X10-kg/6.02X1023mo1
K=R/NA=1.38X10-23 R = 8.314472(15) J·K−1·mol−1 O2 m = 32X10-3 kg/6.02X1023mol-1

上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY 10.2 Microstates and Macrostates ·宏观态 体系的状态由几个状态参数如温度、体积和内能来描述。 An isolated system at equilibrium at a given volume. ·微观态 需表征体系中所有粒子的状态,如所有分子的能量和速度。 Specify the position and velocity of all of the molecules in the system Macrostates:Characterized by a few state variables,such as T,P,internal energy Microstates:Characterize the state of all the particles in the system
10.2 Microstates and Macrostates Macrostates: Characterized by a few state variables, such as T, P, internal energy Microstates: Characterize the state of all the particles in the system
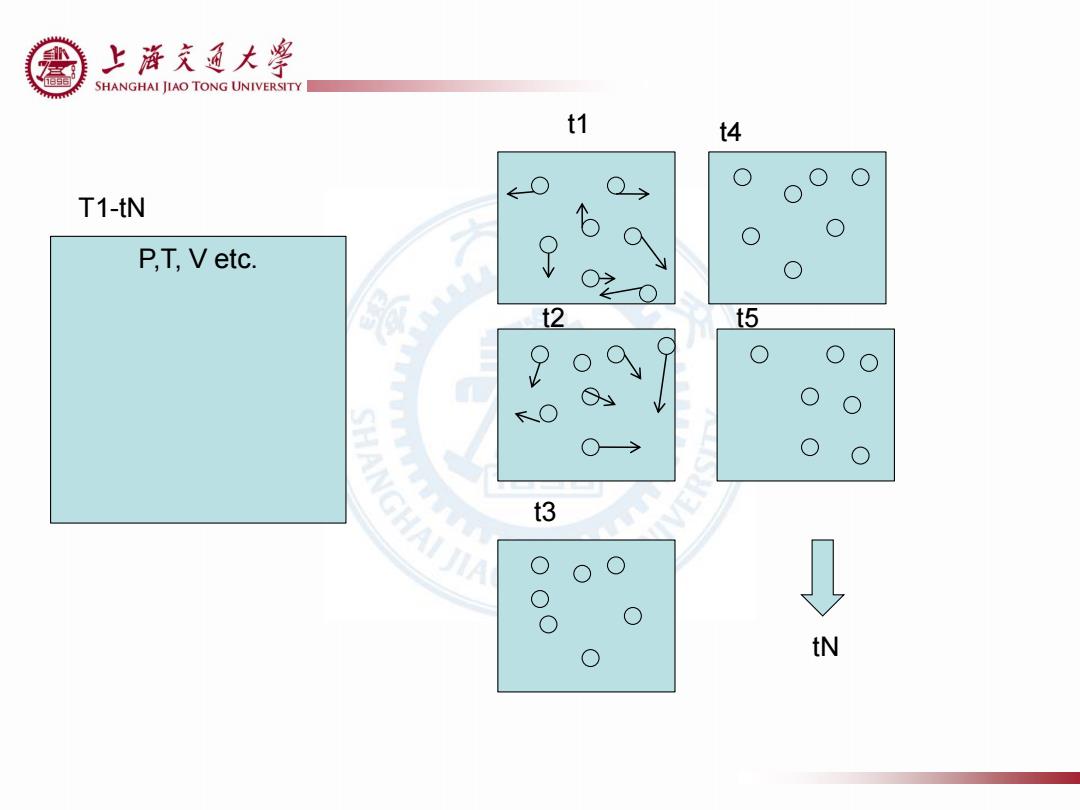
上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY t1 t4 T1-tN P.T,V etc. t5 SHANGHAUIA t3 Q o tN
P,T, V etc. t1 t2 t3 t4 t5 tN T1-tN

上游充通大粤 SHANGHAI JIAO TONG UNIVERSITY 10.2 Microstates and Macrostates In order to compute the macroseopic average of a property .The property of each microstate .Which microstates the system can be in .The probability that the system will be in a given microstate The macroscopic pressure equals to the time average of the Macrostate: instantaneous pressure stating the total number of particles in each box yields Macroscopic pressure Microstate: each way of realizing a given macro distribution Instantaneous pressure Each macrostate may be realized by a number of microstates Time> Figure 10.2 Instantaneous gas pressure as a function of time.(The magnitude of the variation of instantaneous gas pressure is exag- gerated for emphasis.)
10.2 Microstates and Macrostates The macroscopic pressure equals to the time average of the instantaneous pressure