
上游充通大粤 SHANGHAI JIAO TONG UNIVERSITY Chapter 9.Phase Diagram Contents today: .Freezing point depression .The lever rule .Simple Eutectic diagram .Cooling curves AO TONG Peng Zhang Nov 18th,2016
Chapter 9. Phase Diagram Contents today: •Freezing point depression •The lever rule •Simple Eutectic diagram •Cooling curves Peng Zhang Nov 18th , 2016 1
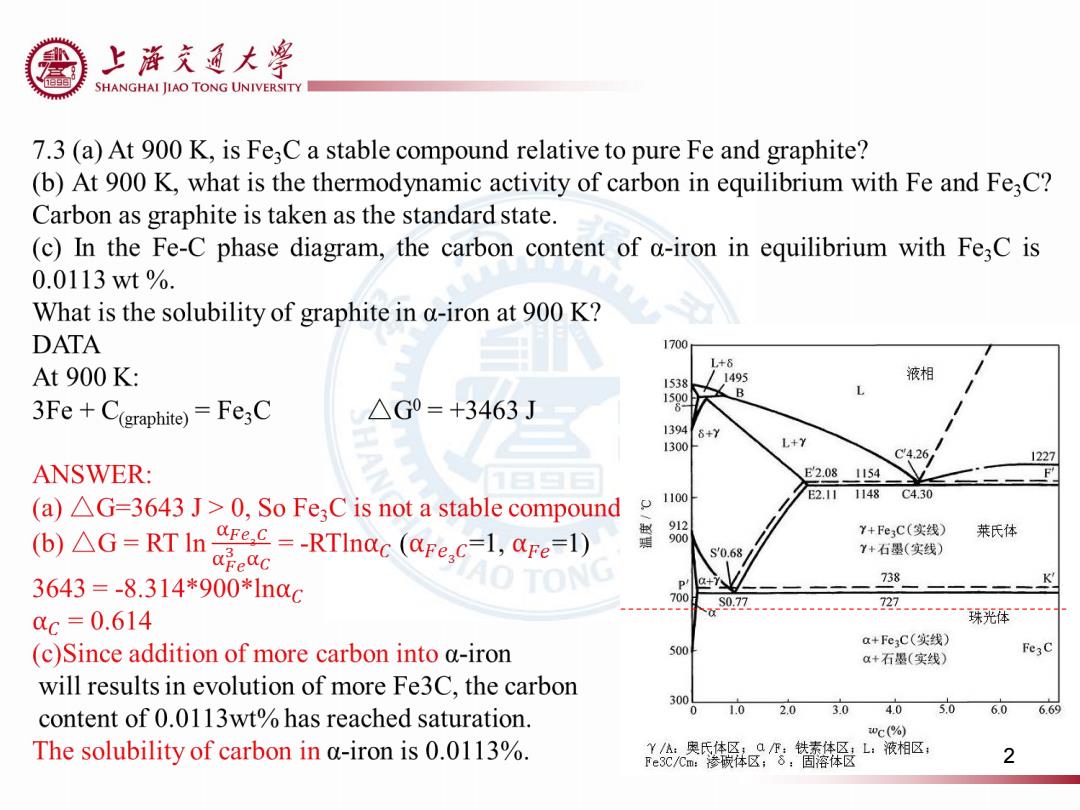
上浒充通大率 SHANGHAI JIAO TONG UNIVERSITY 7.3(a)At 900 K,is Fe;C a stable compound relative to pure Fe and graphite? (b)At 900 K,what is the thermodynamic activity of carbon in equilibrium with Fe and Fe;C? Carbon as graphite is taken as the standard state. (c)In the Fe-C phase diagram,the carbon content of a-iron in equilibrium with Fe3C is 0.0113wt%. What is the solubility of graphite in a-iron at 900 K? DATA 1700 L+8 At 900 K: 1538 1495 液相 3Fe+C(graphite)=Fe3C △G0=+3463J 13946+Y 1300f L+Y C4.26 1227 ANSWER: E2.081154 1100 E2.11 1148 C4.30 (a)AG=3643 J>0,So Fe;C is not a stable compound (b)AG=RT In ec=-RTInac (@Fe.c-1,aFe=1) Y+Fe3C(实线) 莱氏体 apeQc s'0.68 Y+石墨(实线) 3643=-8.314*900*1n0c 738 700 S0.77 727 cc=0.614 珠光体 a+Fe3C(实线) (c)Since addition of more carbon into a-iron 500 a+石墨(实线) Fe3C will results in evolution of more Fe3C,the carbon 300 content of 0.0113wt%has reached saturation. 0 1.0 2.0 3.0 4.0 5.0 6.0 669 wC(%) The solubility of carbon in a-iron is 0.0113%. Y/A:奥氏体区;QF:铁素体区:L:液相区: Fe3C/Cm:渗碳体区;8:固溶体区 2
2

上游充通大粤 SHANGHAI JIAO TONG UNIVERSITY Review:Phase rule Therefore,for a system with N species and P phase: The components C=N-R (R:the number of relationships among the species) p/kPa B AR=P(C-1)+2 水 (液相) REL=C(P-1) 22090 F=VAR-REL-C-P+2 冰 (固相) 蒸发线 For one component system:C=1101.3s 汽 Single phase:P=1,F=2 0.611 (气相) 升华线 0 Two-phase region:P=2,F=1 Triple point:P=3,F=0 273.16373.15 647.29TK 3
Therefore, for a system with N species and P phase: The components C = N – R (R: the number of relationships among the species) VAR = P(C-1) +2 REL = C(P-1) F = VAR-REL=C-P+2 For one component system: C = 1 Single phase: P =1, F = 2 Two-phase region: P = 2, F = 1 Triple point: P = 3, F = 0 Review: Phase rule 3

上游充通大粤 e SHANGHAI JIAO TONG UNIVERSITY Binary System In condensed systems,modest variations in pressure In general system containing do not appreciably alter phase relationships gases,pressure is important Degrees of freedom available in the system(F): F=C-P+1 F=C-P+2 F:the number of system variables that we may freely vary,or arbitrarily fix C:components P:phase C=2 P=1,F=2 单相区 P=2,F=1 平衡线包围的两相区 P=3,F=0 三相平衡线 4
In condensed systems, modest variations in pressure do not appreciably alter phase relationships In general system containing gases, pressure is important 4

上游充通大粤 SHANGHAI JIAO TONG UNIVERSITY 9.1 Freezing point depression(1) The Gibbs free energy change from solid to liquid: partial molar AG=RTIn=RTname G molar f ∫s,pure T △G=RTIna,pwe Liquid 个 if dspue=1 Liquid and solid Tm(melting are at equilibrium temperature) At Tm,solid and liquid are at equilibrium, Solid AG=0,therefore,a.pure-1 at temperatures below Tm UJIAO TONG UMA ACineling-AIm-TASmc=L-TASg Phase diagram of a single- component system L:latent heat of fusion熔解潜热 Assume AHl and AS are independent of temperature AtTm,△melting=0=>L=Tm△Smelting 5
9.1 Freezing point depression (1) if 1 ln ln ln , , , , s pure l pure s pure l pure s l a G RT a f a RT f f G RT Tm(melting temperature) T Liquid Solid Phase diagram of a single- component system Liquid and solid are at equilibrium The Gibbs free energy change from solid to liquid : At Tm, solid and liquid are at equilibrium, ΔG = 0, therefore, Gmelting H melting TS melting L TS melting 1 al, pure L: latent heat of fusion 熔解潜热 at temperatures below Tm Assume ΔH and ΔS are independent of temperature At Tm, ΔGmelting = 0 => L = Tm ΔSmelting G G partial molar molar 5

上浒充通大粤 SHANGHAI JIAO TONG UNIVERSITY 9.1 Freezing point depression(2) L=Tm△Smelting 及是 →ASmelting=L/Tm L(T-T) Tm AGmelting =RTIn apme as.pure RTIn- L(T-T) T1 The subcooled liquid is not stable,super active.The activity is larger than 1,the normal liquid 6
9.1 Freezing point depression (2) L = Tm ΔSmelting ΔSmelting = L/Tm m m . , . , melting m m melting ( - ) ln ln ( - ) (1 T L T T a a RT a a G RT T L T T T T G L s pure l pure s pure l pure m ) T1 The subcooled liquid is not stable, super active. The activity is larger than 1, the normal liquid 6

上浒充通大粤 e SHANGHAI JIAO TONG UNIVERSITY Consider the case where B is added into A to form a solution. Liquid:ideal solution Solid:immiscible T→x Equilibrium:Pure solid A and solution AB at T' Solid A Solution AB A XB→ B A:pure solid--solution Fig.9.2 Plot of the activity of Aliquid AO TONG at T<TmA versus composition. A:pure solid-=pure liquid = solution Melting Dissolving L(T-T) △G=RTln A.soluion To a1.pure 7
>1 Consider the case where B is added into A to form a solution. Liquid: ideal solution Solid: immiscible Equilibrium: Pure solid A and solution AB at T’ l pure l solution a a G RT . , ln Solid A Solution AB A: pure solidsolution A: pure solidpure liquid Melting m m melting ( - ) T L T T G 7 Dissolving solution
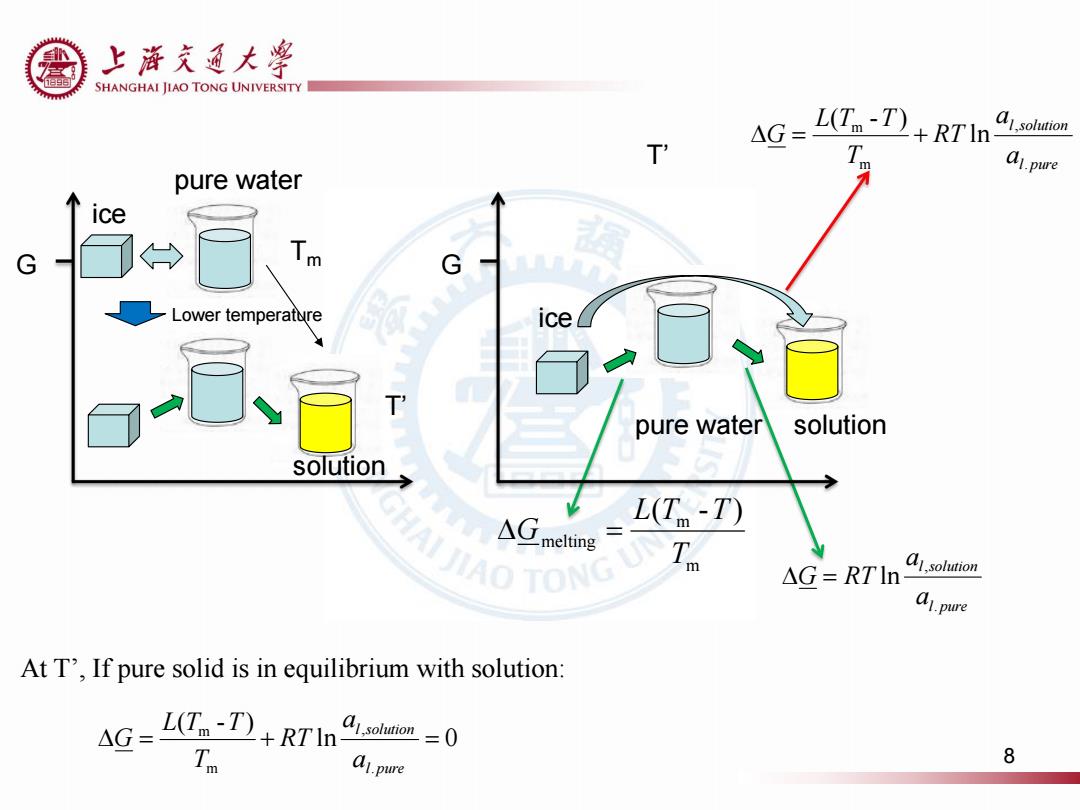
上游充通大粤 SHANGHAI JIAO TONG UNIVERSITY L(n-I)+RTI T 4G m a1.pure pure water ice G G Lower temperature ice pure water solution solution NAIJIAO TONG △G L(T-T) elting △G=RTln a1,solution a1.pure At T',If pure solid is in equilibrium with solution: AG=L(T-)+RTIn bon=0 A1.pure 8
T’ G ice ice pure water solution l pure l solution a a G RT . , ln m m melting ( - ) T L T T G G l pure l solution a a RT T L T T G . , m m ln ( - ) ln 0 ( - ) . , m m l pure l solution a a RT T L T T G At T’ , If pure solid is in equilibrium with solution: Tm pure water solution T’ Lower temperature 8
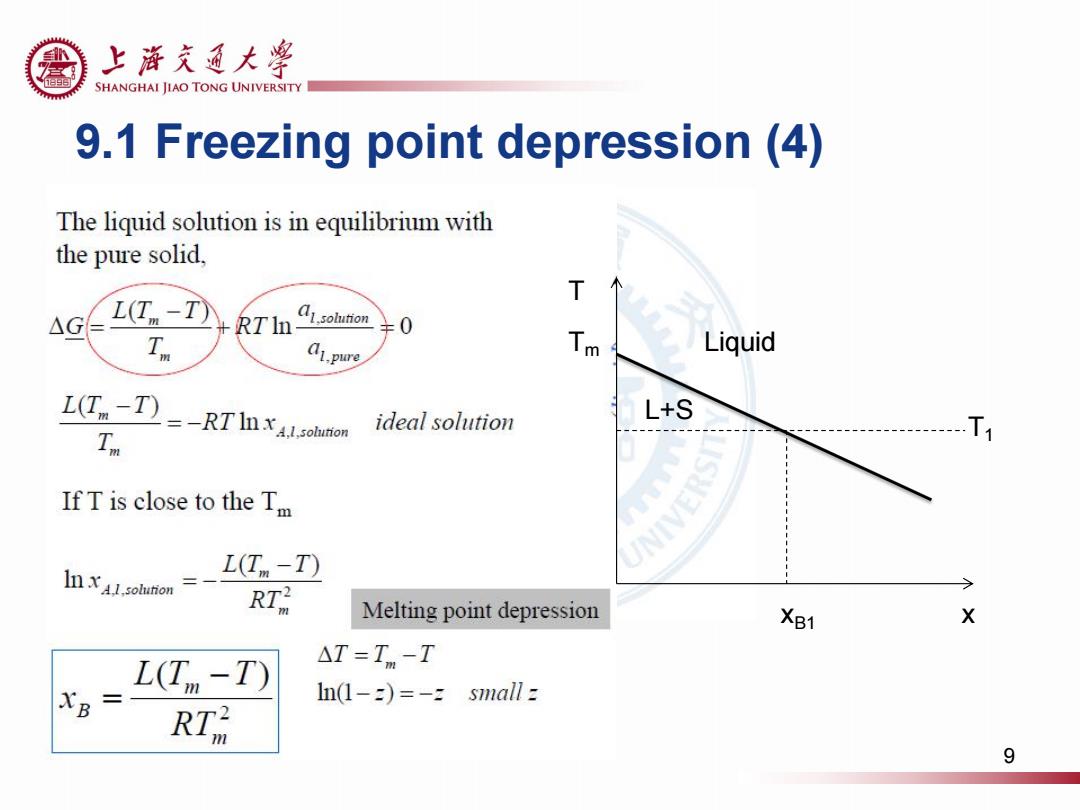
上游充通大粤 SHANGHAI JIAO TONG UNIVERSITY 9.1 Freezing point depression (4) The liquid solution is in equilibrium with the pure solid. T △G L(T-T RTIolunon T a1.pure 人 Liquid L(T-T )=-RT ohunon ideal solution L+S Tn If T is close to the Tm NIVE In x1.solution L(T-T) RT Melting point depression XB1 X L(T -T) △T=Tm-T XB 三 n1-2)=-zs7 nall z RT品 9
9.1 Freezing point depression (4) Tm T Liquid L+S T1 xB1 x 9

上游充通大粤 SHANGHAI JIAO TONG UNIVERSITY 9.1 Freezing point depression(5) L(Tn -T) Example: XB 1mol%of lead added to silver caused lowering of RT melting point of silver. Tm=1234K,L=11300J/mol 4T= R(T)'xa8 314*12342*0.01 T L 11300 =112K Liquid Phase rule: L+S -T F=C-P+1=2-2+1=1 Therefore,once the temperature is specified,the composition is also fixed. XB1 X What about the quantifies of the phases? 10
9.1 Freezing point depression (5) Tm T Liquid L+S T1 xB1 x Example: 1mol% of lead added to silver caused lowering of melting point of silver. Tm = 1234 K, L = 11300 J/mol K L R T x T B 11.2 11300 ( ) 8.314*1234 *0.01 2 2 m Phase rule: F = C – P + 1 = 2 – 2 + 1 = 1 Therefore, once the temperature is specified, the composition is also fixed. What about the quantifies of the phases? 10