
5化学平衡 Chemical ea △,G=-RTInK9 5.0引言(introduction可 研究化学平衡的意义: 1.用热力学方法研究在反应条件下的反应方向和极限 产率; 2.改变温度得到更大的平衡转化率,或温度不变时改 变压力、物料配比等,得到更大的产率; 3通过理论计算同实际生产对比,估计提高产率的 幅度,实现最优化的反应工艺条件
2 5 化学平衡 Chemical equilibrium 5.0 引言 (introduction) 研究化学平衡的意义: 1.用热力学方法研究在反应条件下的反应方向和极限 产率; 2.改变温度得到更大的平衡转化率,或温度不变时改 变压力、物料配比等,得到更大的产率; 3.通过理论计算同实际生产对比,估计提高产率的 幅度,实现最优化的反应工艺条件。 Δr Gm≤0(T,p,W’=0) θ θ ∆rGm = −RT ln K
5.1化学反应的吉布斯函数变化 The Gibbs energy of chemical reactions 复习 aA+bB=cC+dD 反应进度 Extent of reaction,ξ 0=V1A1+V2A2+..+VA+. △n1 △n2 △n=ξ Vi 表示反应进行的程度,称为反应进。 3
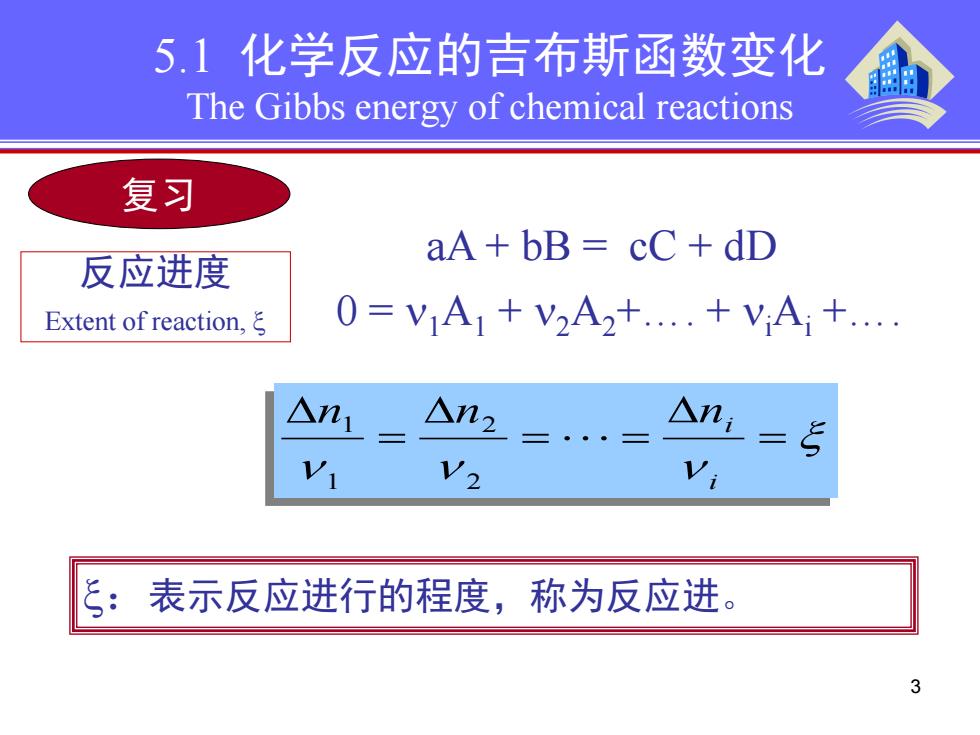
3 5.1 化学反应的吉布斯函数变化 The Gibbs energy of chemical reactions 复习 反应进度 Extent of reaction, ξ aA + bB = cC + dD 0 = ν1A1 + ν2A2+…. + νi Ai +…. ξ ν ν ν = ∆ = ⋅⋅⋅ = ∆ = ∆ i n n ni 2 2 1 1 ξ:表示反应进行的程度,称为反应进
5.1化学反应的吉布斯函数变化 The Gibbs energy of chemical reactions 一个mol反应 反应进行到△n,恰好为各自的计量系数所示的数 量时,称发生了一个mol反应。 △ni =5=1 任意反应微小进程时: dni :d Vi
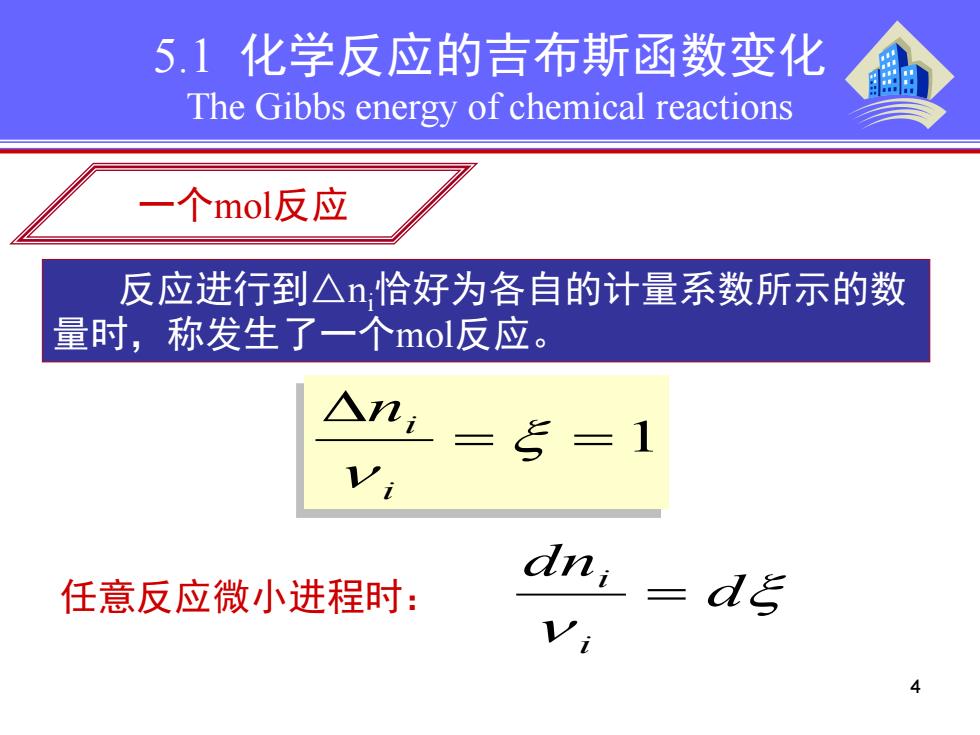
4 5.1 化学反应的吉布斯函数变化 The Gibbs energy of chemical reactions 一个mol反应 φ 反应进行到△ni 恰好为各自的计量系数所示的数 量时,称发生了一个mol反应。 = = 1 ∆ ξ ν i ni ξ ν d dn i i 任意反应微小进程时: =

5.1化学反应的吉布斯函数变化 The Gibbs energy of chemical reactions 摩尔反应吉布斯函数变△,Gm The mole reaction Gibbs energy 在一定T、p和组成不变的条件下,1mol反应的 吉布斯函数变,即(oG/O)1p称为摩尔反应吉布斯函 数变,用△Gn表示。 △,Gm &G 判别化学反应方向 T.P △Gm≤0(Tp,W'=0) 5
5 5.1 化学反应的吉布斯函数变化 The Gibbs energy of chemical reactions 一. 摩尔反应吉布斯函数变Δr Gm The mole reaction Gibbs energy 在一定T、p和组成不变的条件下,1mol反应的 吉布斯函数变,即(∂G/∂ξ)T,P称为摩尔反应吉布斯函 数变,用Δr Gm表示。 T P r m G G , ∂ ∂ ∆ = ξ 判别化学反应方向 Δr Gm≤0(T,p,W’=0)
5.1化学反应的吉布斯函数变化 The Gibbs energy of chemical reactions A=-△,Gm aG A称为化学亲和势, 即反应推动力。 T.P 自发 A=-A,Gm≥0 平衡衡
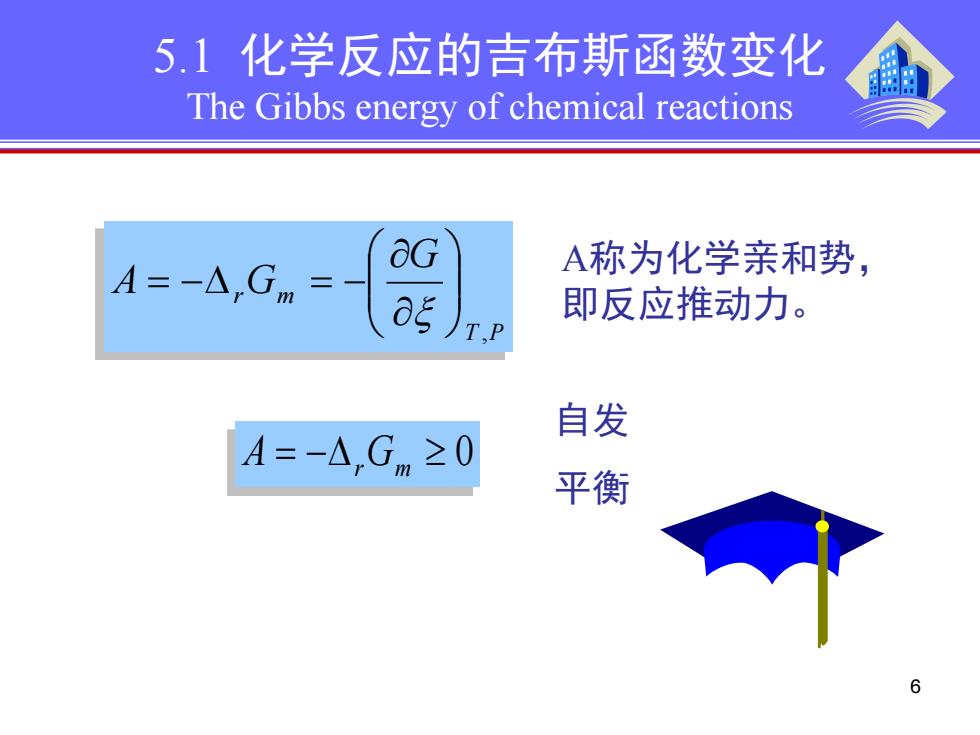
6 T P r m G A G , ∂ ∂ = −∆ = − ξ A称为化学亲和势, 即反应推动力。 = −∆ ≥ 0 A rGm 自发 平衡 5.1 化学反应的吉布斯函数变化 The Gibbs energy of chemical reactions
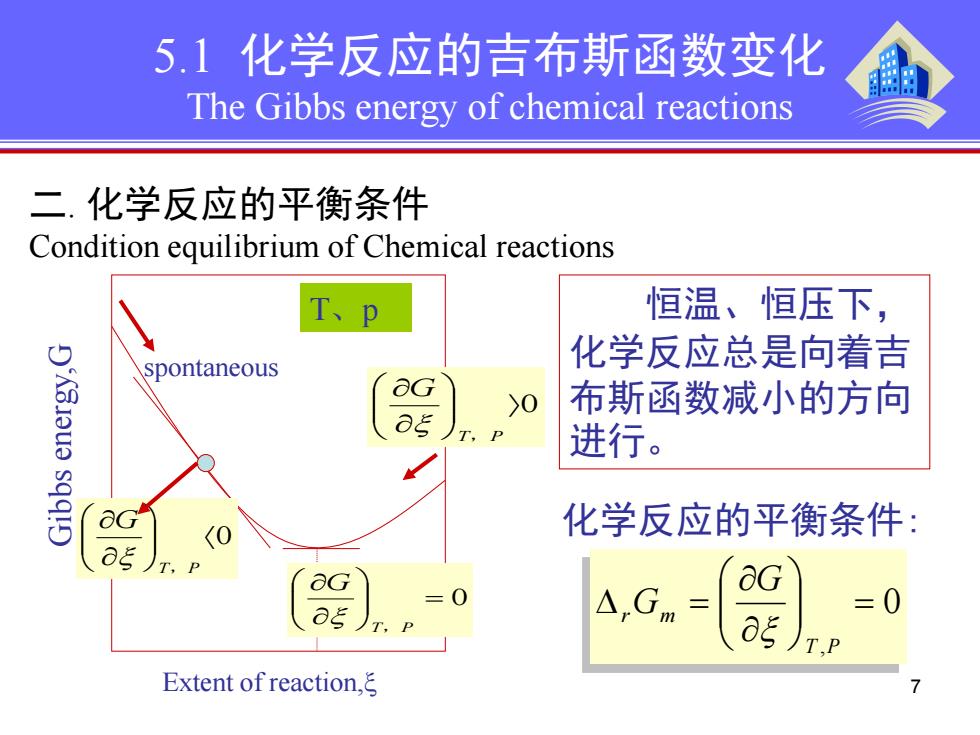
5.1化学反应的吉布斯函数变化 The Gibbs energy of chemical reactions 二.化学反应的平衡条件 Condition equilibrium of Chemical reactions T、p 恒温、恒压下, spontaneous 化学反应总是向着吉 >0 布斯函数减小的方向 进行。 化学反应的平衡条件: =0 △,Gm =0 Extent of reaction,ξ
7 5.1 化学反应的吉布斯函数变化 The Gibbs energy of chemical reactions 恒温、恒压下, 化学反应总是向着吉 布斯函数减小的方向 进行。 化学反应的平衡条件: Gibbs energy,G Extent of reaction,ξ 〈0 ∂ ∂ T P G , ξ T、p spontaneous 〉0 ∂ ∂ T P G ξ , = 0 ∂ ∂ T P G ξ , 二. 化学反应的平衡条件 Condition equilibrium of Chemical reactions 0 , = ∂ ∂ ∆ = T P r m G G ξ

5.2理想气体等温方程及标准平衡常数 Isothermal equation of perfect gas and the standard equilibrium constant 一、 理想气体化学反应等温方程 Chemical reactions Isothermal equation of perfect gas A,G.=A,G。+RTIh AGm-A.Gm+RTInJp 任意反应: aA(g)+bB(g)=cC(g)+dD(g)
8 5.2 理想气体等温方程及标准平衡常数 Isothermal equation of perfect gas and the standard equilibrium constant 一、理想气体化学反应等温方程 Chemical reactions Isothermal equation of perfect gas B p p G G RT B r m r m ν ∆ = ∆ + ln ∏ φ φ 任意反应: aA(g) + bB(g) = cC(g) + dD(g) b B a A d D c C P p p p p p p p p J = θ θ θ θ ∆r Gm =∆r Gm +RTlnJP φ φ

4.5.2理想气体等温方程及标准平衡常数 Isothermal equation of perfect gas and the standard equilibrium constant Tp,W'-0时:△,Gm=△Ga+RTln Jp可判别方向。 任意反应:aA(g)+bB(g)=cC(g)+dD(g) 1.△Gm>0 反应向左反应;←一 2.△Gm<0反应向右反应; → 3.△,Gm=0反应达成平衡。 9
9 4.5.2 理想气体等温方程及标准平衡常数 Isothermal equation of perfect gas and the standard equilibrium constant 1. ∆r Gm>0 反应向左反应;← 2. ∆r Gm<0 反应向右反应;→ 3. ∆r Gm=0 反应达成平衡。 T,p,W’=0时:∆r Gm= ∆r Gm +RTln JP 可判别方向。 φ 任意反应:aA(g) + bB(g) = cC(g) + dD(g)

5.2理想气体等温方程及标准平衡常数 Isothermal equation of perfect gas and the standard equilibrium constant 二.理想气体反应标准平衡常数 The standard equilibrium constant of perfect gas reaction 化学反应平衡 △.Gm=0 △,Gm=AGm+RTln(Jp)平衡=0 AGm-RTln(Jp)平衡=-RTInK A,Gm=-RTInK 定义 Kp=K:理想气体化学反应标准平衡常数 10
10 二.理想气体反应标准平衡常数 The standard equilibrium constant of perfect gas reaction 5.2 理想气体等温方程及标准平衡常数 Isothermal equation of perfect gas and the standard equilibrium constant 化学反应平衡 ∆r Gm=0 ∆r Gm =∆r Gm +RTln(JP ) 平衡 = 0 φ 定义 ∆r Gm = - RTln(JP ) 平衡 = - RTlnKP φ φ KP = K : 理想气体化学反应标准平衡常数 φ φ ∆r Gm = - RTlnK φ φ

52理想气体等温方程及标准平衡常数 Isothermal equation of perfect gas and the standard equilibrium constant 计算△,Gm函数的方法 由有关反应计算A,Gm 已知:C0(石墨)+02(g)-C02(g) AGm (1) C0(g)+1/202(g)=C02(g) △,Gm(2) 可得:C(石墨十1/202(g-C0(g)△,Gm(3)F△Gm(1)△,Gm(2) C(石墨)+C02(g)F2C0(g)△,Gm(4)=△,Gm(1)2△,Gm(2) 11
11 计算∆r Gm函数的方法 一、由有关反应计算∆r Gm 已知:CO(石墨)+O2(g)=CO2(g) ∆r Gm (1) CO(g)+1/2O2(g)= CO2(g) ∆r Gm(2) 可得:C(石墨)+1/2O2(g)=CO(g) ∆r Gm(3)= ∆r Gm (1)- ∆r Gm (2) C(石墨)+ CO2(g)= 2CO(g) ∆r Gm (4) = ∆r Gm (1)-2 ∆r Gm (2) φ 5.2 理想气体等温方程及标准平衡常数 Isothermal equation of perfect gas and the standard equilibrium constant φ