
本节基本要求 ·理解附加压力的概念及其与表面张力的关系。 理解拉普拉斯公式及开尔文公式的应用。 ·理解亚稳状态与新相生成的关系。 4上一内容 下一内容 ◇回主目录 ←返回 2011/12/23
上一内容 下一内容 回主目录 返回 2011/12/23 本节基本要求 • 理解附加压力的概念及其与表面张力的关系。 • 理解拉普拉斯公式及开尔文公式的应用。 • 理解亚稳状态与新相生成的关系

§10一2弯曲表面下的附加压力及其后果 (Additional pressure under curved surface) 一、附加压力的产生 以液体表面为例 P外 A B 平面AB,受力平衡,p=P外 4上一内容 下一内容 ◇回主目录 ←返回 2011/12/23
上一内容 下一内容 回主目录 返回 2011/12/23 §10-2 弯曲表面下的附加压力及其后果 (Additional pressure under curved surface) 一、附加压力的产生 以液体表面为例 A B p p外 平面AB,受力平衡,p=p外
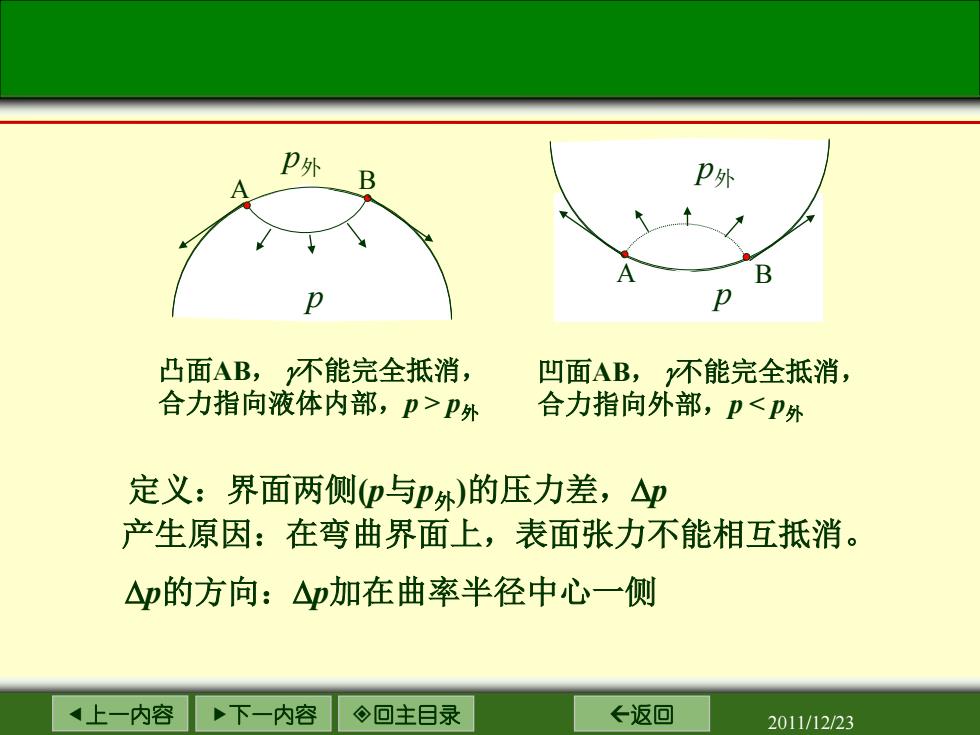
P外 B P外 B 凸面AB,y不能完全抵消, 凹面AB,不能完全抵消, 合力指向液体内部,P>P外 合力指向外部,卫<P外 定义:界面两侧D与P外)的压力差,△p 产生原因:在弯曲界面上,表面张力不能相互抵消。 △p的方向:△p加在曲率半径中心一侧 上一内容 下一内容 ◇回主目录 ←返回 2011/12/23
上一内容 下一内容 回主目录 返回 2011/12/23 A B p p外 凸面AB, γ不能完全抵消, 合力指向液体内部,p > p外 A B p p外 凹面AB, γ不能完全抵消, 合力指向外部,p < p外 定义:界面两侧(p与p外)的压力差,∆p 产生原因:在弯曲界面上,表面张力不能相互抵消。 ∆p的方向:∆p加在曲率半径中心一侧
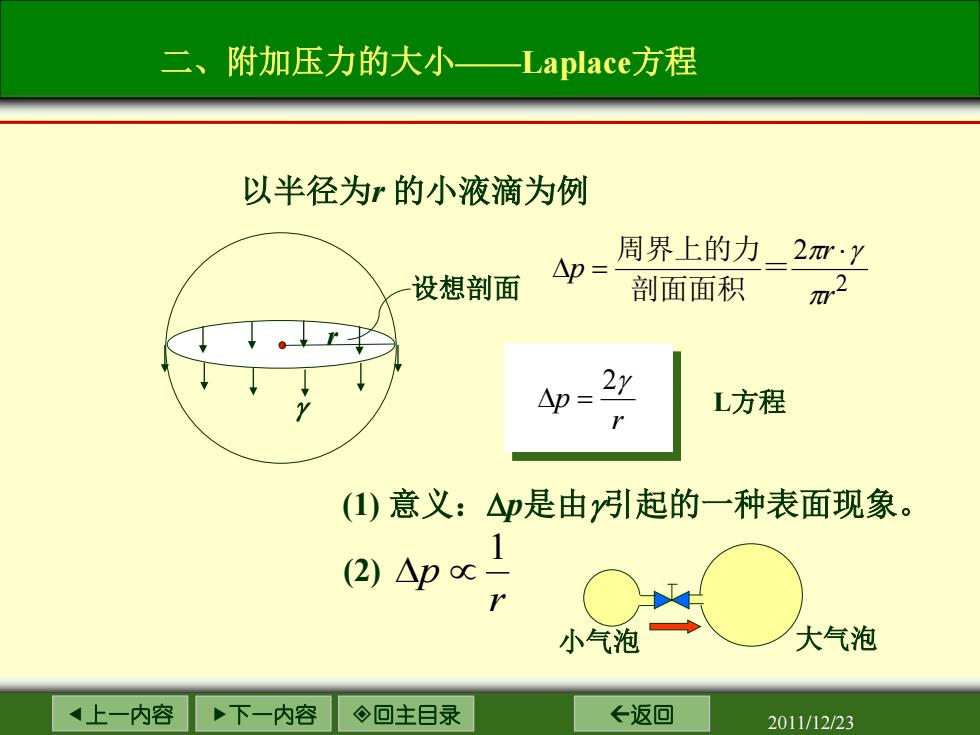
二、附加压力的大小一Laplace方程 以半径为r的小液滴为例 周界上的力_2m·y 设想剖面 △p= 剖面面积 Ap= L方程 (1)意义:△p是由y引起的一种表面现象。 2)p 1 小气泡 大气泡 4上一内容 。下一内容 ◇回主目录 ←返回 2011/12/23
上一内容 下一内容 回主目录 返回 2011/12/23 r γ 设想剖面 二、附加压力的大小——Laplace方程 以半径为r 的小液滴为例 2 2 r r p π π ⋅γ ∆ = = 剖面面积 周界上的力 r p 2γ ∆ = L方程 (1) 意义:∆p是由γ引起的一种表面现象。 (2) r p 1 ∆ ∝ 小气泡 大气泡
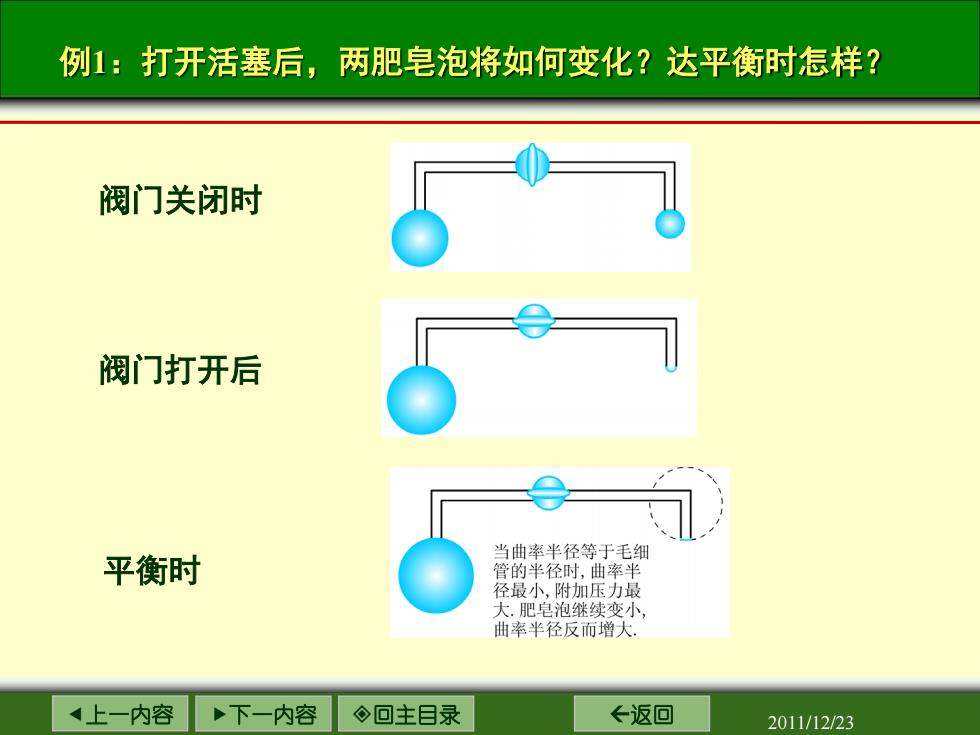
例1:打开活塞后,两肥皂泡将如何变化?达平衡时怎样? 阀门关闭时 阀门打开后 当曲率半径等于毛细 平衡时 管的半径时,曲率半 径最小,附加压力最 大.肥皂泡继续变小 曲率半径反而增大 上一内容 下一内容 ◇回主目录 ←返回 2011/12/23
上一内容 下一内容 回主目录 返回 2011/12/23 例1:打开活塞后,两肥皂泡将如何变化?达平衡时怎样? 阀门关闭时 阀门打开后 平衡时

(3)对由液膜形成的气泡,L方程为 △p 4r (4)其他弯曲界面的L方程: △p= 2-g=2s」=21L1=2s=s r r 例2:室温时小水滴,r=1mm时,△p≈200Pa(1.5mmHg) r=10-5mm时,△p≈145p9 ∴.当颗粒半径可用mm描述时,可忽略△p;当颗粒 半径小至不可用mm描述时(超细粉,纳米材料), 由于△D值巨大,会使液、固体许多性质发生巨变, 与正常液、固体不同。 4上一内容 下一内容 ◇回主目录 ←返回 2011/12/23
上一内容 下一内容 回主目录 返回 2011/12/23 (3) 对由液膜形成的气泡,L方程为 r p 4γ ∆ = (4) 其他弯曲界面的L方程: r r r r p s g 2 s l 2 l l 2 s s 2 − − − − ∆ = = = = γ γ γ γ 例2:室温时小水滴,r =1mm时, ∆p≈200Pa (1.5mmHg) r =10-5mm时, ∆p≈145pθ ∴ 当颗粒半径可用mm描述时,可忽略∆p;当颗粒 半径小至不可用mm描述时(超细粉,纳米材料), 由于∆p值巨大,会使液、固体许多性质发生巨变, 与正常液、固体不同
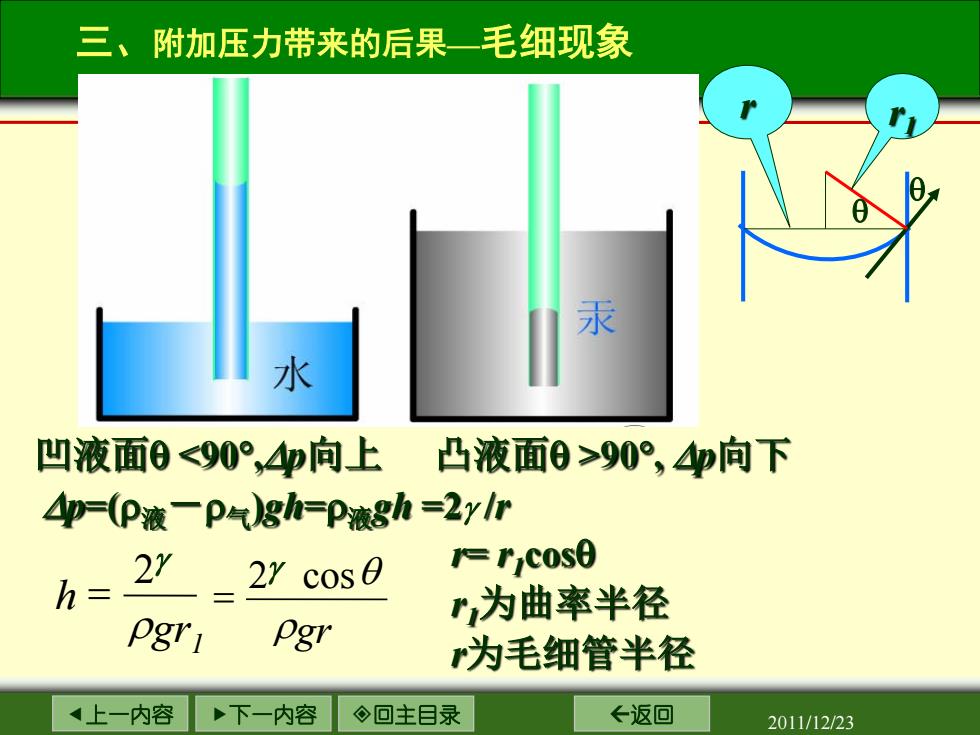
三、附加压力带来的后果一毛细现象 汞 水 凹液面090°,4向下 4p=(P液一p气gh=P液8h=2ylr h=2”- 27 cos0 r,cos0 ,为曲率半径 pgr Pgr r为毛细管半径 上一内容 下一内容 ◇回主目录 ←返回 2011/12/23
上一内容 下一内容 回主目录 返回 2011/12/23 凹液面θ 90° , ∆p向下 ∆p=(ρ液-ρ气)gh=ρ液gh =2γ /r r= r1cosθ r1为曲率半径 r为毛细管半径 θ θ r1 r gr1 h ρ γ2 = 2 cos ρgr γ θ = 三、附加压力带来的后果—毛细现象
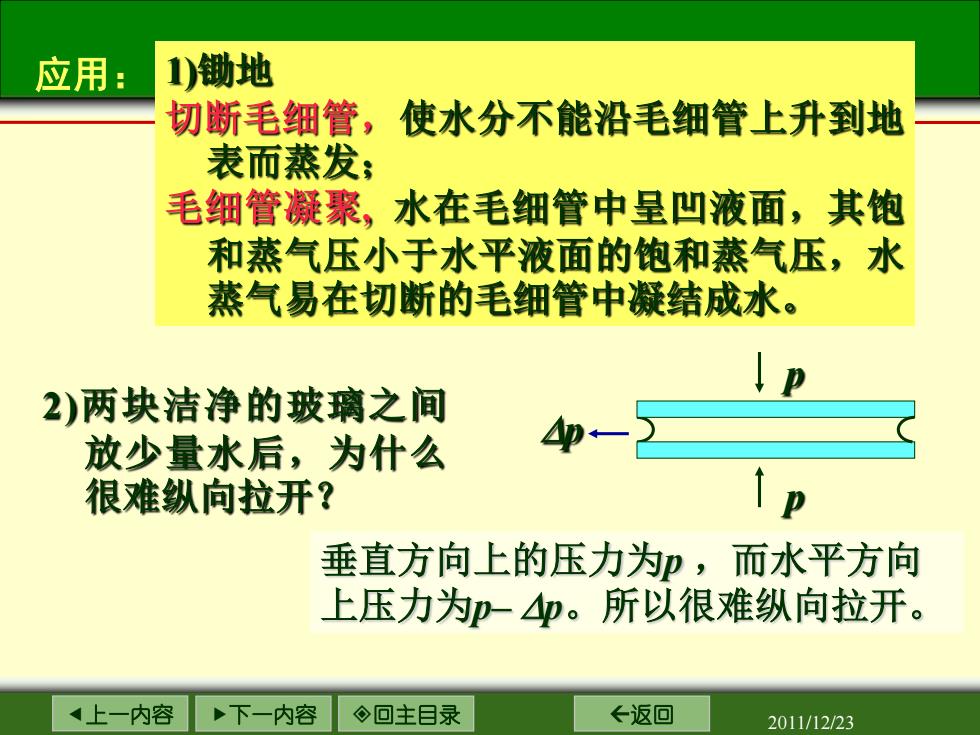
应用: 1)锄地 切断毛细管,使水分不能沿毛细管上升到地 表而蒸发; 毛细管凝聚,水在毛细管中呈凹液面,其饱 和蒸气压小于水平液面的饱和蒸气压,水 蒸气易在切断的毛细管中凝结成水。 \P 2)两块洁净的玻璃之间 放少量水后,为什么 Ap+ 很难纵向拉开? I P 垂直方向上的压力为p,而水平方向 上压力为p-仰。所以很难纵向拉开。 上一内容 。下一内容 ◇回主目录 ←返回 2011/12/23
上一内容 下一内容 回主目录 返回 2011/12/23 应用: 1)锄地 切断毛细管,使水分不能沿毛细管上升到地 表而蒸发; 毛细管凝聚, 水在毛细管中呈凹液面,其饱 和蒸气压小于水平液面的饱和蒸气压,水 蒸气易在切断的毛细管中凝结成水。 2)两块洁净的玻璃之间 放少量水后,为什么 很难纵向拉开? p p ∆p 垂直方向上的压力为p ,而水平方向 上压力为p– ∆p。所以很难纵向拉开

四、附加压力带来的后果一微小液滴的饱和蒸气压 开尔文方程 定性说明:在一定T和(p外)下,当液滴半 >黄 径r很小时,压力很大,其很高,从而 蒸气压增大。 > 定量计算:在一定T和p外下,半径为r的 液滴的蒸气压为pv,则 dpy dp 嗡 RTPv 4上一内容 下一内容 ◇回主目录 ←返回 2011/12/23
上一内容 下一内容 回主目录 返回 2011/12/23 定性说明:在一定T和(p外)下,当液滴半 径r很小时,压力p很大,其µ很高,从而 蒸气压增大。 定量计算:在一定T和p外下,半径为r的 液滴的蒸气压为 pV,则 v l m g m l v m d d RT p V V V p p = = • 四、附加压力带来的后果—微小液滴的饱和蒸气压 • —开尔文方程

dpy= Vm dp= T dp外+w)=w=2a Py RT RT RT 即 :,:正常值) In 2W.1 p RT r In 2. 2yM Kelvin方程 p RTpr 4上一内容 下一内容 ◇回主目录 ←返回 2011/12/23
上一内容 下一内容 回主目录 返回 2011/12/23 ∫ ∫ →∞ ⋅ = r r p p RT r V p p 1 d d 2 l m v v v γ o v 即 (pv o:正常值) RT r V p p 2 1 ln l v m = ⋅ γ o v RT r M p p ρ 2γ ln v = o v RT r V p RT V p p RT V p RT V p p 1 d 2 d d( ) d d l m l m l m l m v v ⋅ γ = = 外 + ∆ = ∆ = Kelvin方程