电子科技大学：《导波场论 Field Theory of Guided Waves》课程教学资源（课件讲稿）第一章 电磁场的基本理论（2/3）

导波场论 第一章电磁场的基本理论(2)

导波场论 第一章 电磁场的基本理论(2)

1.6边界条件的一般表达式 ∮i-00) en×(i1-i2)=j ∮d-s en×(E-E2)=0 ∮B.dS=0 en·(B-B2)=0 ∮，D.ds=∫pdW en·(D-D)=Ps e 分界面上的电荷面密度 媒质1 媒质2 分界面上的电流面密度 导波场论

                 n S n n n S e D D e B B e E E e H H J ( )  ( ) 0 ( ) 0 ( ) 1 2 1 2 1 2 1 2              n e  媒质1 媒质2 分界面上的电荷面密度 分界面上的电流面密度 d ( ) d d d d 0 d C S C S S S V D H l J S t B E l S t B S D S ρdV                                              1.6边界条件的一般表达式 导波场论 2

1.6边界条件的推证 ()电磁场量的法向边界条件 在两种媒质的交界面上任取 煤质1 一点P,作一个包围点P的扁 媒质2 平圆柱曲面S,如图表示。 令△h→0，则由 ∮，D.ds=9 (D-D.)AS=PsAS 即 en·(D-D2)=Ps 同 ∮、Bd5=0 e·(B-B)=0 理 导波场论 3

1.6边界条件的推证 导波场论 (1)电磁场量的法向边界条件 令Δh →0，则由 ΔS D1  D2  n e  媒质1 媒质2 Δh S P 在两种媒质的交界面上任取 一点P，作一个包围点P 的扁 平圆柱曲面S，如图表示。 d S D S  q     n 1 2 ( ) S e  D  D      1 2 n ( ) D D S  e S   S    即 同 理 d 0 S B S      n 1 2 e (B B )  0    3

1.6边界条件的推证 (1)电磁场量的切向边界条件 在介质分界面两侧，选取如图所示的小环路，令△h→0， nd-0)d →(i,-i)△I=j、·N△1 △i=N×en△1 →(H1-i2)△=(H1-i2)(N×e)△M =[en×(H,-H】V△M 媒质1 故 ×(i,-H2)=Jj。 媒质2 同理 en×(E-E2)=0 导波场论

1.6边界条件的推证 导波场论 (1)电磁场量的切向边界条件 在介质分界面两侧，选取如图所示的小环路，令Δh →0， d ( ) d C S D H l J S t               n 1 2 e (E  E )  0    1 2 ( ) H H S  l  J Nl      即 同理 n l  N e l    1 2 1 2 n (H H )l  (H H )(Ne )l        Δl H1  H2  n e  媒质1 媒质2 N  Δh n 1 2 [e (H H )]Nl     n 1 2 ( ) S e  H H  J     故 4

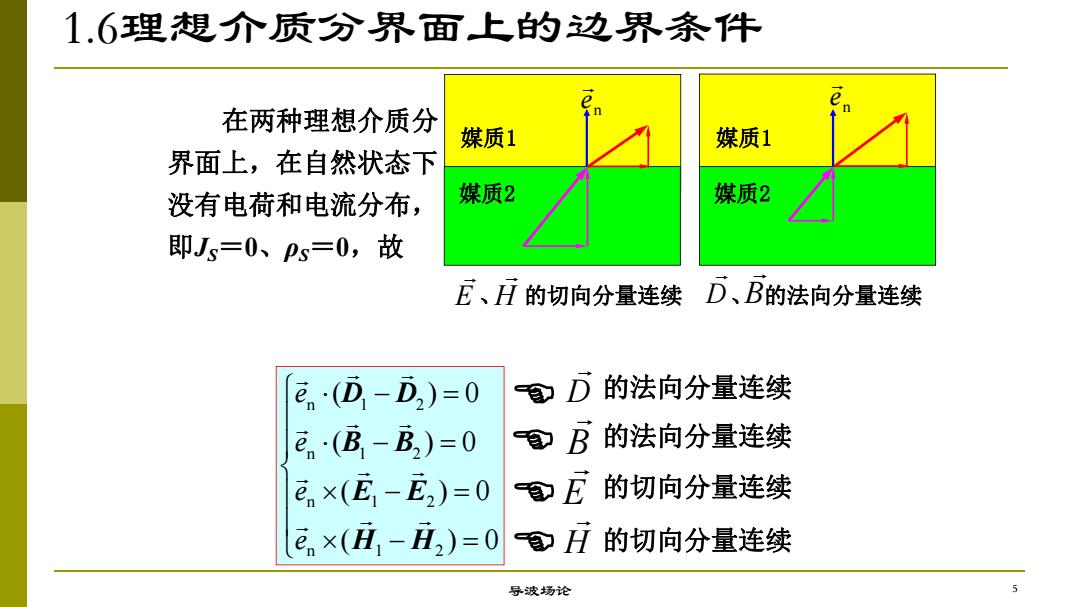
1.6理想介质分界面上的边界条件 在两种理想介质分 媒质1 媒质1 界面上，在自然状态下 没有电荷和电流分布， 媒质2 媒质2 即Js=0、ps=0,故 E、五的切向分量连续 D、B的法向分量连续 e(D-D2)=0 D 的法向分量连续 e(B-B2)=0 自 B的法向分量连续 en×(E-E2)=0 E的切向分量连续 en×(H1-H2)=0 H的切向分量连续 导波场论

n 1 2 n 1 2 n 1 2 n 1 2 ( ) 0 ( ) 0 ( ) 0 ( ) 0 e e e e                              D D B B E E H H 在两种理想介质分 界面上，在自然状态下 没有电荷和电流分布， 即JS＝0、ρS＝0，故 D 的法向分量连续   B 的法向分量连续   E 的切向分量连续   H 的切向分量连续   n e  媒质1 媒质2 D 、 的法向分量连续  B  n e  媒质1 媒质2 E 、 的切向分量连续  H  1.6理想介质分界面上的边界条件 导波场论 5

1.6理想导体表面上的边界条件 口理想导体：电导率为无限大的导电媒质 ▣ 特征：电磁场在理想导体内恒为零 设媒质2为理想导体，则E2、D2、H2、 理想导体 B2均为零，故 en·D=ps @①理想导体表面上的电荷密度等于D的法向分量 en·B=0 理想导体表面上B的法向分量为0 en×E=0 理想导体表面上E的切向分量为0 en×i=jg a 理想导体表面上的电流密度等于的切向分量 导波场论

1.6理想导体表面上的边界条件 导波场论 n n n n 0 0 S S e D e B e E e H J                        设媒质2为理想导体，则E2、D2、H2、 B2均为零，故 p 理想导体：电导率为无限大的导电媒质 p 特征：电磁场在理想导体内恒为零 理想导体 D  S J  H  理想导体表面上的电荷密度等于D 的法向分量   理想导体表面上B 的法向分量为0   理想导体表面上 E 的切向分量为0   理想导体表面上的电流密度等于 H 的切向分量   6

1.6良导体的边界条件 口对于非理想的良导体，只要电导率足够高，就可以近似认为电磁场 分布在导体的表面。在表面上电场和磁场的切向分量满足以下关系 Z、=Es/i×Hs ▣可以用来近以描述一：金属波导或谐振腔内物向场的比例关系 Z、=R+Xs 良导体公式 Rs=Xs= 20 表面电阻 表面电抗 导波场论

1.6良导体的边界条件 p 对于非理想的良导体，只要电导率足够高，就可以近似认为电磁场 分布在导体的表面。在表面上电场和磁场的切向分量满足以下关系 ： p 可以用来近似描述一般金属波导或谐振腔内切向场的比例关系 导波场论 ZS  ES n  HS  ZS RS S   jX 2 RS XS     表面电阻 表面电抗 良导体公式 7

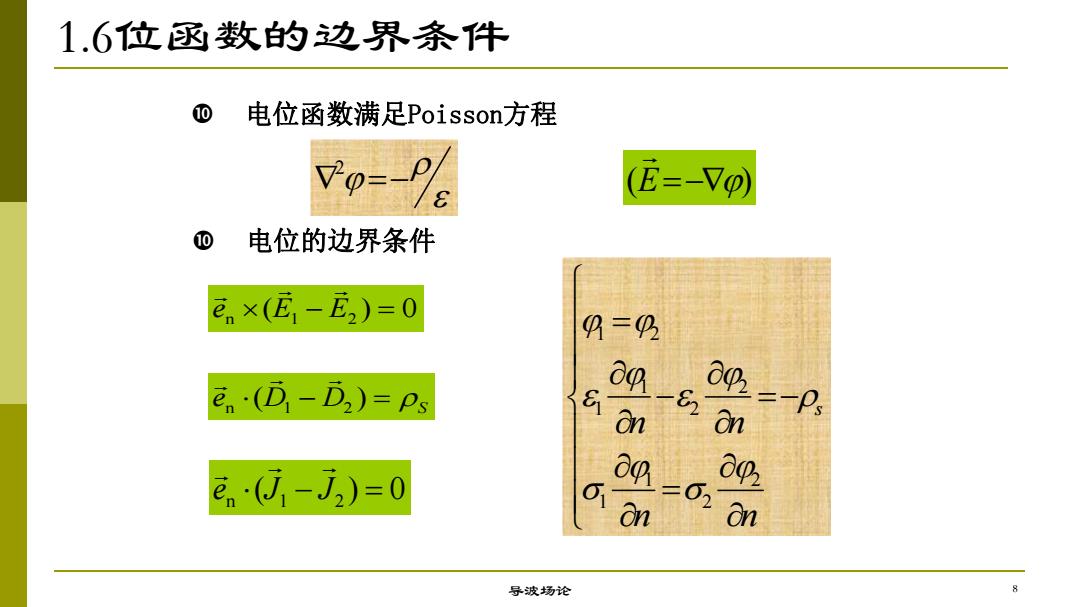
1.6位函数的边界条件 0 电位函数满足Poisson方程 (龙=-V0) 0 电位的边界条件 en×(E,-E2)=0 9=9 en·(D-D2)=Ps on 002 on -P e。j-j2)=0 o o02 On - 20m 导波场论

1.6位函数的边界条件 导波场论  电位函数满足Poisson方程  电位的边界条件 n 1 2 ( ) S e  D  D      n 1 2 e (J  J )  0    n 1 2 e (E  E )  0    2      1 2 1 2 1 2 1 2 1 2 s n n n n                             (E)  8

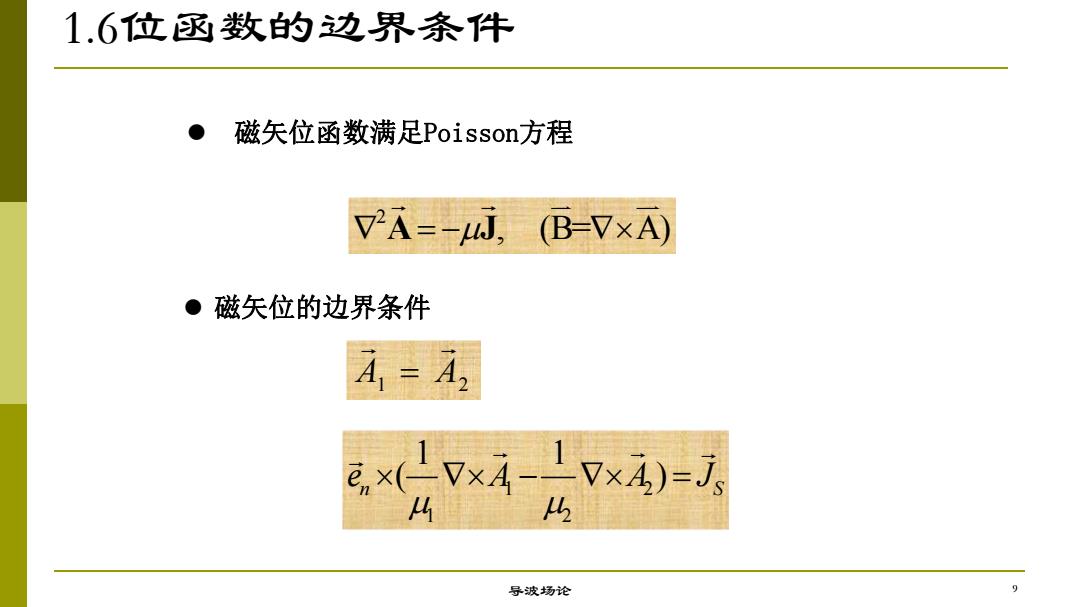
1.6位丞数的边界条件 磁矢位函数满足Poisson方程 VA=-uJ, (B-V×A) ●磁矢位的边界条件 A=4A, e,xv×A-1v×4)=7 4 5 导波场论 9

1.6位函数的边界条件 导波场论 l 磁矢位的边界条件 l 磁矢位函数满足Poisson方程 2  A  J, (B=A)     A1  A2   1 2 1 2 1 1 ( ) n S e A A J            9

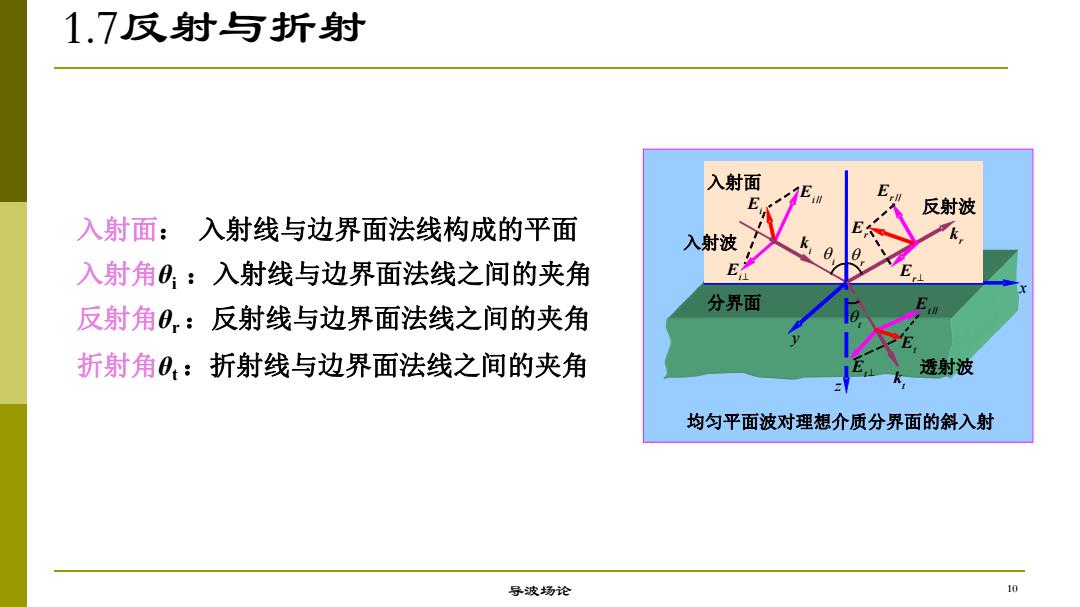
1.7反射与折射 入射面 E 反射波 入射面：入射线与边界面法线构成的平面 入射波 入射角0：入射线与边界面法线之间的夹角 E 分界面 反射角0，：反射线与边界面法线之间的夹角 折射角0：折射线与边界面法线之间的夹角 透射波 均匀平面波对理想介质分界面的斜入射 导波场论 10

1.7反射与折射 导波场论 入射面： 入射线与边界面法线构成的平面 反射角θr：反射线与边界面法线之间的夹角 入射角θi ：入射线与边界面法线之间的夹角 折射角θt：折射线与边界面法线之间的夹角 均匀平面波对理想介质分界面的斜入射 i q r q t q z x y Ei Ei // Ei^ 入射波 反射波 透射波 分界面 入射面 Er// Er^ Er Et^ Et Et // i k r k t k 10