
第六章金属磁性的能带模型理论 前面讨论的理论均假定对磁性有贡献的电子全都局域在原 子核附近。各种交换作用都是近邻原子中电子之间的相互静电 作用称为一局域电子交换模型。其成功之处体现在: ①给出了外斯分子场的本质,解释了铁磁性,反铁磁性, 亚铁磁性,螺磁性的起源,给出了各种磁性材料的高温顺 磁磁化率与温度的关系 ②对于金属盐类及氧化物,磁性原子的磁矩大小均为玻尔 磁子的整数倍,对于过渡金属只是在高温(T>T)情况 下才与实验比较一致。 ③在温度略低于T附近,M、与温度的变化关系(T。-T) 海森伯理论y=1/2。实验上大部分物质y=13;少数为y=1/2
第六章 金属磁性的能带模型理论 前面讨论的理论均假定对磁性有贡献的电子全都局域在原 子核附近。各种交换作用都是近邻原子中电子之间的相互静电 作用称为-局域电子交换模型。其成功之处体现在: ①给出了外斯分子场的本质,解释了铁磁性,反铁磁性, 亚铁磁性,螺磁性的起源,给出了各种磁性材料的高温顺 磁磁化率χ与温度的关系。 ②对于金属盐类及氧化物,磁性原子的磁矩大小均为玻尔 磁子μB的整数倍,对于过渡金属只是在高温 情况 下才与实验比较一致。 ③在温度略低于 Tc附近,Ms与温度的变化关系~ 海森伯理论γ =1/2 。实验上大部分物质γ =1/3;少数为γ =1/2 ( ) T T c T T c

④Fe和Co金属电阻率p在T,附近有转变,dp有极大值。可 以用局域电子自旋无序散射来解释。 ⑤基于局域电子交换模型的自旋波理论成功说明了低温值 发磁化强度与温度关系(T定律)以及色散关系 无法用此模型解释的主要问题: ①3过渡族金属原子的磁矩大小都不是整数 如Fe,Co,Ni分别是2.2g,1.7B’0.6B 以及Cr的复杂情况等
(T T ) c ④Fe和Co金属电阻率 ρ在Tc附近有转变, 有极大值。可 以用局域电子自旋无序散射来解释。 ⑤基于局域电子交换模型的自旋波理论成功说明了低温下自 发磁化强度与温度关系( 定律)以及色散关系 d dT 3 2 T 2 k Dk 无法用此模型解释的主要问题: ①3d过渡族金属原子的磁矩大小都不是整数 如Fe,Co,Ni分别是2.2 μB ,1.7 μB ,0.6 μB 以及Cr的复杂情况等

②铁磁金属(Fε,Co,Ni以及其他金属组成的合金磁矩与成 分的变化有些可用Slater-Pauling曲线表示。 ③对于金属磁性材料,用居里定律中常数C计算原子磁矩 时,得不到半整数S值。 ④在居里点以上,Fε服从海森伯模型。对于Cr而言,显 示出不服从海森伯模型。 因此,实验结果显示,3d电子参与了传导作用,存在传导 电子能带和未填满的3壳层电子能带,导致3d过渡族金属 的磁性表现出多样性:Sc,Ti,V是顺磁性的;Mn,Cr, Y-Fe是反铁磁性的;a-Fe是铁磁性的;Cu,Zn是抗磁性的
②铁磁金属(Fe,Co,Ni)以及其他金属组成的合金磁矩与成 分的变化有些可用Slater-Pauling曲线表示。 ③对于金属磁性材料,用居里定律中常数C计算原子磁矩 时,得不到半整数S值。 ④在居里点以上,Fe服从海森伯模型。对于Cr而言,显 示出不服从海森伯模型。 因此,实验结果显示,3d电子参与了传导作用,存在传导 电子能带和未填满的3d壳层电子能带,导致3d过渡族金属 的磁性表现出多样性:Sc,Ti,V是顺磁性的;Mn,Cr, γ-Fe是反铁磁性的;α-Fe是铁磁性的;Cu,Zn是抗磁性的

从而据此在3d,4s电子在金属的晶格周期场中运动的基础上发展 了巡游电子模型,其主要内容如下: ①巡游电子分布在能带中。Fe,Co,Ni的磁性负载者是3d能带中 的空穴,其磁矩数目由空穴数决定。 ②巡游电子之间相互作用可用分子场近似方法给出分子场H, 与磁化强度成比例:Hm=号nml/4其中m相对磁化强 度,n为每个原子3d能带中空穴数。I为Stoner-Hubband参数, 相应的分子场能量为:E,m=-n2m21 取决于由多体相互作用效应所引起的关联和交换作用 ③在一定温度下,电子在能级中的分布遵从Fermi-Dirac统计
从而据此在3d,4s电子在金属的晶格周期场中运动的基础上发展 了巡游电子模型,其主要内容如下: ①巡游电子分布在能带中。Fe,Co,Ni的磁性负载者是3d能带中 的空穴,其磁矩数目由空穴数决定。 ②巡游电子之间相互作用可用分子场近似方法给出分子场 与磁化强度成比例: 其中 相对磁化强 度,n为每个原子3d能带中空穴数。I为Stoner-Hubband参数, 相应的分子场能量为: I取决于由多体相互作用效应所引起的关联和交换作用 ③在一定温度下,电子在能级中的分布遵从Fermi-Dirac 统计。 H m 1 2 / H nmI m B m 1 2 2 E n m I m 4
§6.1能带模型的物理图象 一、3d,4s电子能带结构 过渡金属中,3d、4s电子看成“自由”地在晶格中巡游,总能 方2k2 量可以写成:E= 电子有效质量m 2m m/m=→ 反映电子在晶格中运动的自由程度。 具有能量为E的电子数目有一分布,用态密度函数 N(E)=轻(2m)3E% E N(E) N(E) N(E) 自由电子态密度(a) 金属中3d,4s电子态 非金属中电子态密度(c) 密度(b)
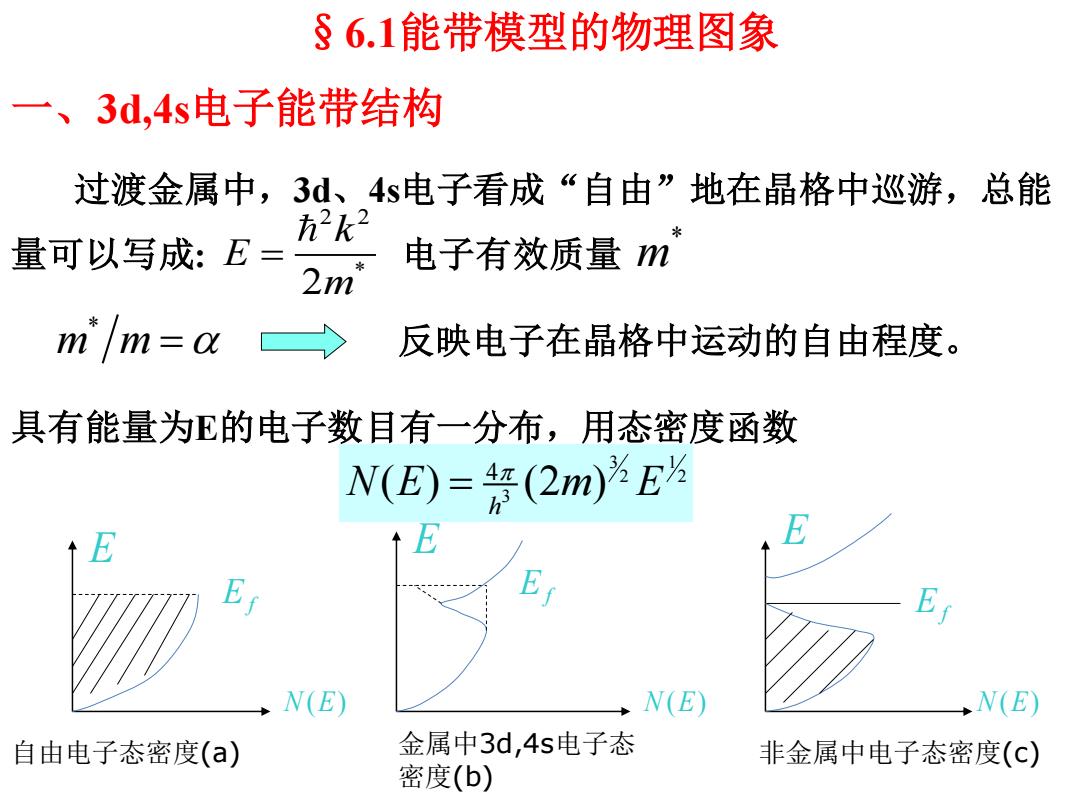
§6.1能带模型的物理图象 一、3d,4s电子能带结构 过渡金属中,3d、4s电子看成“自由”地在晶格中巡游,总能 量可以写成: 电子有效质量 反映电子在晶格中运动的自由程度。 具有能量为E的电子数目有一分布,用态密度函数 2 2 * 2 k E m * m * m m 3 1 2 2 3 4 ( ) (2 ) h N E m E E E E Ef Ef Ef N(E) N(E) N(E) 自由电子态密度(a) 金属中3d,4s电子态 密度(b) 非金属中电子态密度(c)

在晶体中,电子能带交叠,使晶体中电子的能带不再是抛物 线,如(b)、(c),这正由X射线发射谱实验所证实。 二.能带理论对铁磁性自发磁化的解释 态密度函数N(E)=N(E)+N(E) W(E)表示能量为E的自旋向上电子数 W(E)表示能量为E的自旋向下电子数 E △ N.(E) N.(E) N.(E) △N(E) (a) (b)
在晶体中,电子能带交叠,使晶体中电子的能带不再是抛物 线,如(b)、(c),这正由X射线发射谱实验所证实。 二.能带理论对铁磁性自发磁化的解释 态密度函数 表示能量为E的自旋向上电子数 表示能量为E的自旋向下电子数 N E N E N E ( ) ( ) ( ) N E( ) N E( ) E E N (E) N (E) N (E) N (E) (a) (b)

当H=0,不考虑电子间交换作用,则电子自旋磁矩互相抵消,不显示 磁性。(图a) 认为电子间存在正的交换作用,相当于晶体中存在一个沿正方向的 内磁场。因而,具有正向自旋的态密度N(E)所对应的最低能量 要比N(E)对应的要低,产生能带劈裂△,其大小与电子间交 换作用有直接联系(图b)。因而N(E)和W_(E)在Ex之下所具 有的电子总数不等。所以N(E)中空穴比N(E)中空穴数目要 少。这种空穴数目未抵消的情况相当于一个原子中未被抵消的自旋 数目,但它不一定是整数,这时可能发生自发磁化。至于铁磁性还 是反铁磁性,将由交换作用决定
当H=0,不考虑电子间交换作用,则电子自旋磁矩互相抵消,不显示 磁性。(图a) 认为电子间存在正的交换作用,相当于晶体中存在一个沿正方向的 内磁场。因而,具有正向自旋的态密度 所对应的最低能量 要比 对应的要低,产生能带劈裂 ,其大小与电子间交 换作用有直接联系(图b)。因而 和 在 之下所具 有的电子总数不等。所以 中空穴比 中空穴数目要 少。这种空穴数目未抵消的情况相当于一个原子中未被抵消的自旋 数目,但它不一定是整数,这时可能发生自发磁化。至于铁磁性还 是反铁磁性,将由交换作用决定。 N E( ) N E( ) N E( ) N E( ) Ef N E( ) N E( )
3d,4s能带中电子分布 元素 电子组态 按能带理论电子分布 未填满空穴数 未抵消自旋数 3d+ 3d- 4s+ 4s 3d* 3d- Cr 3d4s 2.7 2.7 0.3 0.3 2.3 2.3 0 Mn 3d54s2 3.2 3.2 0.3 0.3 1.8 1.8 0 Fe 3d64s2 4.8 2.6 0.3 0.3 0.2 2.4 2.2 Co 3d74s2 5.0 3.3 0.35 0.35 0 1.7 1.7 Ni 3d84s2 5.0 4.4 0.3 0.3 0 0.6 0.6 Cu 3d04s 5.0 5.0 0.5 0.5 0 0 0
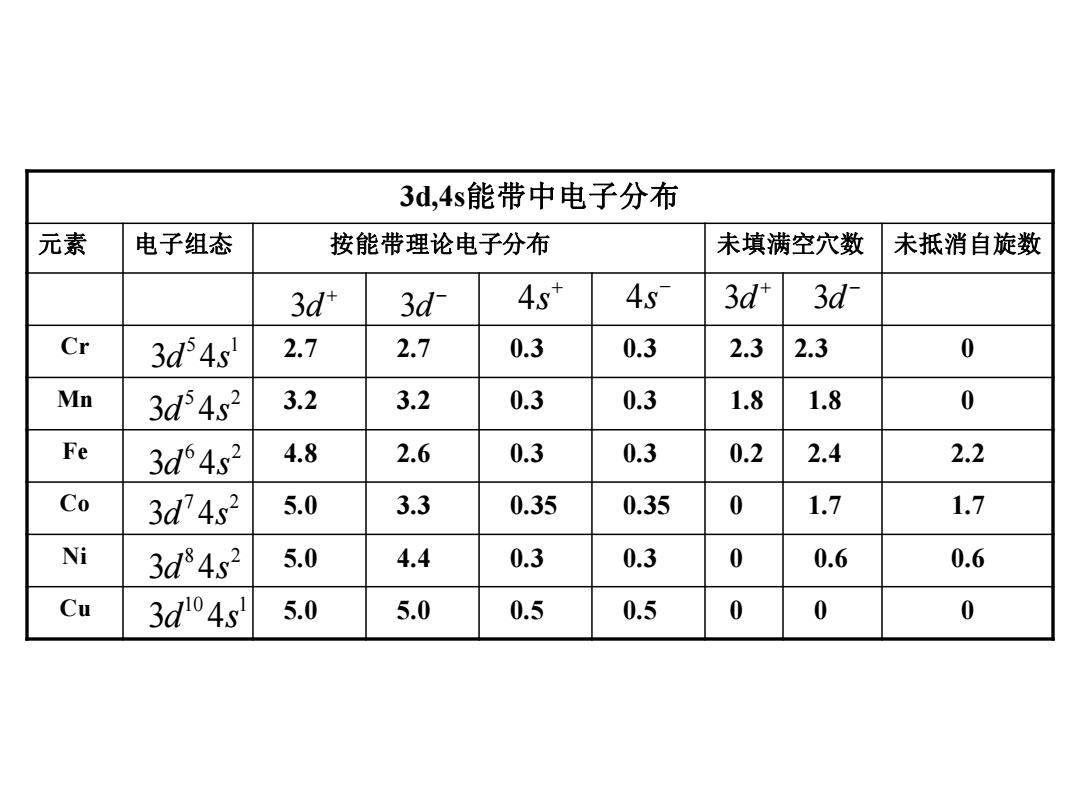
3d,4s能带中电子分布 元素 电子组态 按能带理论电子分布 未填满空穴数 未抵消自旋数 Cr 2.7 2.7 0.3 0.3 2.3 2.3 0 Mn 3.2 3.2 0.3 0.3 1.8 1.8 0 Fe 4.8 2.6 0.3 0.3 0.2 2.4 2.2 Co 5.0 3.3 0.35 0.35 0 1.7 1.7 Ni 5.0 4.4 0.3 0.3 0 0.6 0.6 Cu 5.0 5.0 0.5 0.5 0 0 0 3d 3d 3d 3d 4s 4s 5 1 3 4 d s 5 2 3 4 d s 6 2 3 4 d s 7 2 3 4 d s 8 2 3 4 d s 10 1 3 4 d s
§6.2斯托纳能带模型 体系Hamilton: E 考虑N个原子,每个原子有n个准自由电 子(3d、4s)在金属晶格中巡游,自旋 △ △ 简并的能带在交换作用下发生分裂。 N.(E) N(E) 月=i,+∑i0 Z R Ho=∑T,CaCo .(2) r y R X
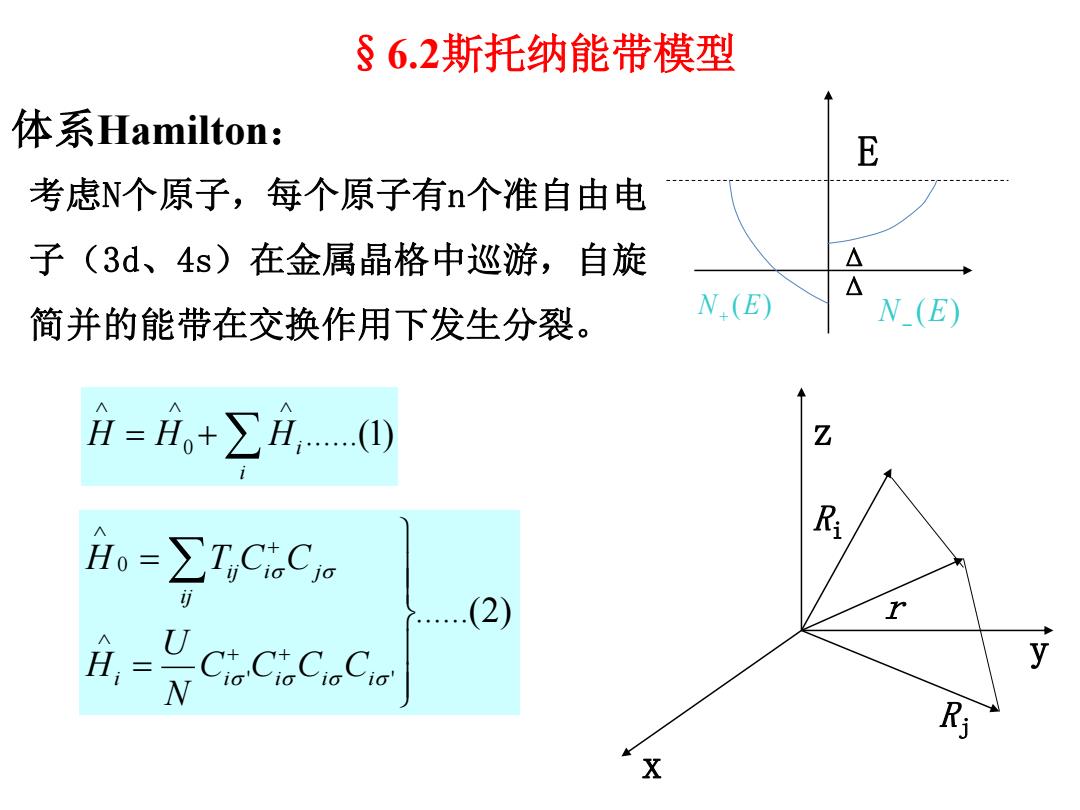
§6.2斯托纳能带模型 体系Hamilton: 0 ......(1) i i H H H x y z ......(2) ' ' 0 i i i i i j ij ij i C C C C N U H H T C C N (E) E N (E) Δ Δ 考虑N个原子,每个原子有n个准自由电 子(3d、4s)在金属晶格中巡游,自旋 简并的能带在交换作用下发生分裂。 Ri r Rj
T,j功G-R克V+-R山 .(3) u-j。-Rpg记R)e-R0.c2Raw C。第i个原子自旋σ电子产生算符,表象转换 e.-i c .H=∑CiCio(4) R /X R
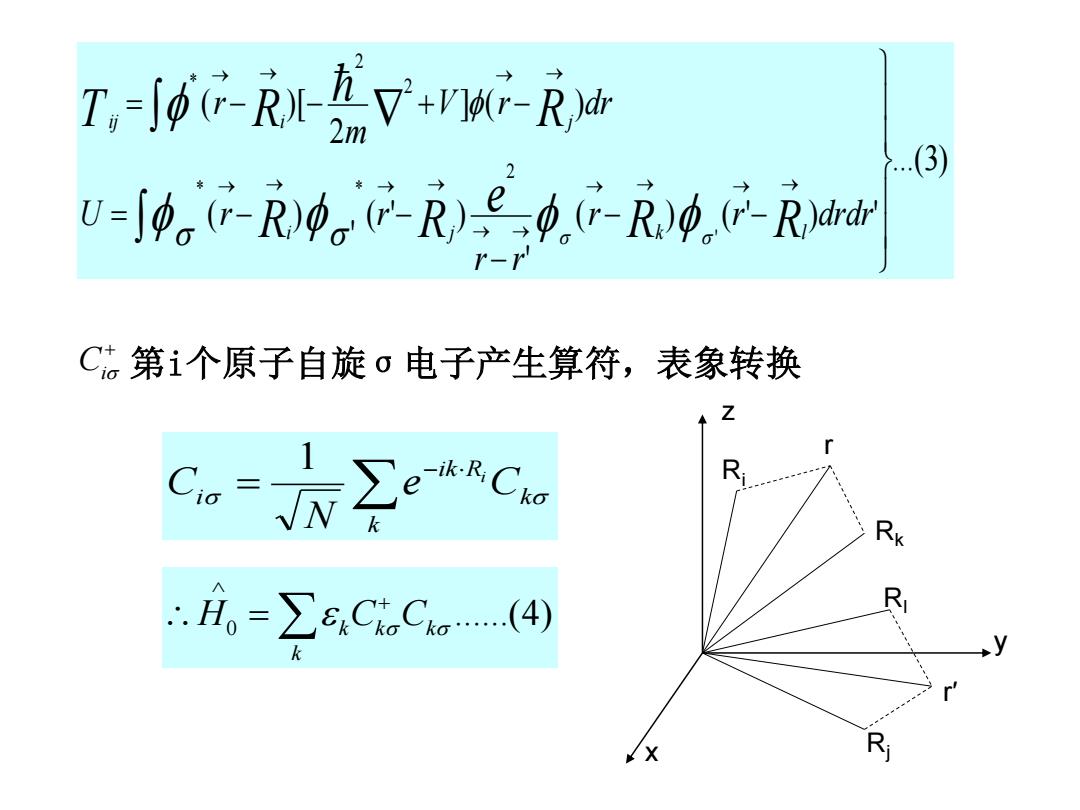
Ci 第i个原子自旋σ电子产生算符,表象转换 0 ......(4) k k k k H C C k k ik R i e C N C i 1 z x y Ri Rk Rl Rj r r′ ...(3) ( ) ( ' ) ' ' ( ' ) ' ( ) ] ( ) 2 ( )[ ' 2 * * 2 2 * r r drdr r r U r r V r dr m r R R e R R T R R i j k l ij i j