
第二章 原子的磁性及物质的顺磁性 第一节 电子的轨道磁矩和自旋磁矩 第二节 原子磁矩 第三节 稀土及过渡元素的有效玻尔磁子 第四节 轨道角动量的冻结(晶体场效应) 第五节 朗之万顺磁性理论 返回 结束放映
第一节 电子的轨道磁矩和自旋磁矩 第二节 原子磁矩 第三节 稀土及过渡元素的有效玻尔磁子 第四节 轨道角动量的冻结(晶体场效应) 第五节 朗之万顺磁性理论 返回 结束放映 第二章 原子的磁性及物质的顺磁性
第一节 电子的轨道磁矩和自旋磁矩 物质的磁性来源于原子的磁性,研究原子磁性是研究 物质磁性的基础。 原子的磁性来源于原子中电子及原子核的磁矩。 原子核磁矩很小,在我们所考虑的问题中可以忽略。 电子磁矩(轨道磁矩、自旋磁矩)一→原子的磁矩。 即: 电子轨道运动产 生电子轨道磁矩 构成原子 物质磁性 电子自旋产生电 的总磁矩 的起源 子自旋磁矩
第一节 电子的轨道磁矩和自旋磁矩 物质的磁性来源于原子的磁性,研究原子磁性是研究 物质磁性的基础。 原子的磁性来源于原子中电子及原子核的磁矩。 原子核磁矩很小,在我们所考虑的问题中可以忽略。 电子磁矩(轨道磁矩、自旋磁矩) ——→原子的磁矩。 即: 电子轨道运动产 生电子轨道磁矩 电子自旋产生电 子自旋磁矩 构成原子 的总磁矩 物质磁性 的起源

原子的电子壳层与磁性 a.原子中基态电子的分布:用四个量子数n、1、m、m,来 规定每个电子的状态,每组量子数代表一个状态,只允许 有一个电子处于该状态。一组、1量子数相同的电子的状 态是简并的
a. 原子中基态电子的分布:用四个量子数n、l、ml、ms来 规定每个电子的状态,每组量子数代表一个状态,只允许 有一个电子处于该状态。一组n、l量子数相同的电子的状 态是简并的。 原子的电子壳层与磁性
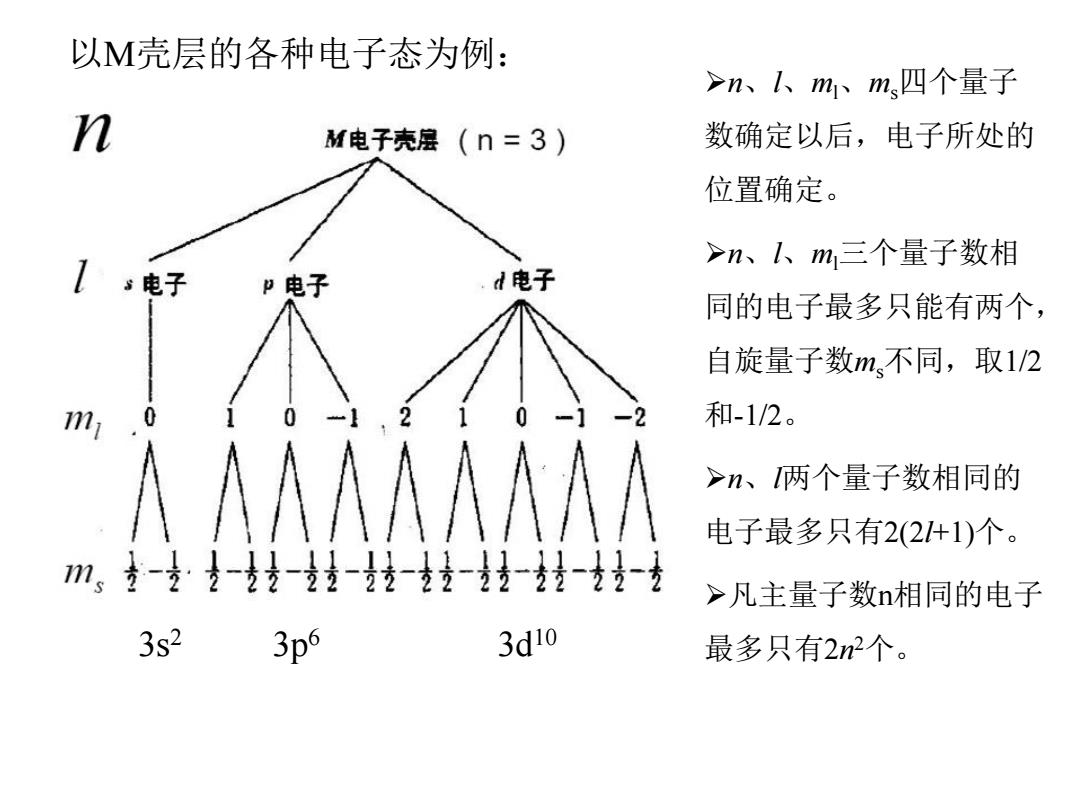
以M壳层的各种电子态为例: >n、1、m、m,四个量子 n M电子壳层(n=3) 数确定以后,电子所处的 位置确定。 >n、1、m三个量子数相 1s电子 p电子 .d电子 同的电子最多只能有两个, 自旋量子数m、不同,取1/2 1m1 0 -2 和-1/2。 >n、两个量子数相同的 电子最多只有2(2什1)个。 m,寺-支:为-多-方黄-在-支方-为-拉-支-老 >凡主量子数n相同的电子 3s2 3p6 3d10 最多只有2n2个
3s2 3p6 3d10 以M壳层的各种电子态为例: n、l、ml、ms四个量子 数确定以后,电子所处的 位置确定。 n、l、ml三个量子数相 同的电子最多只能有两个, 自旋量子数ms不同,取1/2 和-1/2。 n、l两个量子数相同的 电子最多只有2(2l+1)个。 凡主量子数n相同的电子 最多只有2n 2个

b.原子中电子基态分布服从规则: 泡利不相容原理 能量最小原理 c.电子填充方式(依电子组态能量高低) 基态原子的电子在原子轨道中填充的顺序是: 1s,2s,2p,3s,3p,4s,3d,4p,5s,4d,5p,6s,4f,5d,6p,7s,5f,6d IA-IA IA-VAIB一VB 铜系 周期 IB-IB 铜系 大多数原子 7s 7p 7 基态的电子组态 6p 6d 6 遵循此规律。 5d 5f 5 少数元素有 4d 4f 些变化,如: 3 Cu:…3d10,4s 2 Cr:…3d5,4s 1
b. 原子中电子基态分布服从规则: 泡利不相容原理 能量最小原理 c. 电子填充方式(依电子组态能量高低) 10 1 5 1 u 3d ,4s Cr 3d , 4s 大多数原子 基态的电子组态 遵循此规律。 少数元素有 些变化,如: C : :

结论: >当电子填满电子壳层时,各电子的轨道运动及自旋取向 占据了所有可能的方向,形成一个球体,因此合成的总动 量矩和总磁矩都为零。 >只有未填满电子的壳层上的电子才会对原子磁矩作出贡 献一这些未满壳层称为磁性电子壳层
结论: 当电子填满电子壳层时,各电子的轨道运动及自旋取向 占据了所有可能的方向,形成一个球体,因此合成的总动 量矩和总磁矩都为零。 只有未填满电子的壳层上的电子才会对原子磁矩作出贡 献——这些未满壳层称为磁性电子壳层

一、电子轨道磁矩(由电子绕核的运动所产生) 由量子力学知:轨道角动量P=√1(1+1)h 乃 2m 令Y1 e, 轨道磁力比 2m 则:4=-y,乃 说明:电子轨道运动产生的磁矩与角动量在数值上成正 比,方向相反。 其中1=0,1,2…n-1,h=3元 4=002方
说明:电子轨道运动产生的磁矩与角动量在数值上成正 比,方向相反。 l l l l l l l l P m e P m e m e P 则: 令 ,轨道磁力比 2 2 2 由量子力学知:轨道角动量 Pl l(l 1) 其中l=0,1,2…n-1 , 2 h m e l l l 2 ( 1) 一、电子轨道磁矩(由电子绕核的运动所产生)

令uB= eh=9.273x10-24[Am2]≈10-23[Am2] 2m (波尔磁子,电子磁矩的基本单位) .4,=V(l+1)4B 对于多电子系统:4,=VL(L+)4。L=∑m 角量子数1=0,1,2.n-1(n个取值) 磁量子数m=0、士1、士2、士3·士1 (2+1个取值) >在填充满电子的次壳层中,各电子的轨道运动分 别占了所有可能的方向,形成一个球体,因此合 成的总角动量等于零,所以计算原子的轨道磁矩 时,只考虑未填满的那些次壳层中的电子一这 些壳层称为磁性电子壳层
l B B l l A m A m m e ( 1) 9.273 10 [ ] 10 [ ] 2 2 4 2 2 3 2 (波尔磁子,电子磁矩的基本单位) 令 角量子数 l=0,1,2…n-1 (n个取值) 磁量子数 ml =0、 ± 1、 ± 2、 ± 3 ∙ ∙ ∙ ∙ ∙ ∙ ±l (2l+1个取值) 在填充满电子的次壳层中,各电子的轨道运动分 别占了所有可能的方向,形成一个球体,因此合 成的总角动量等于零,所以计算原子的轨道磁矩 时,只考虑未填满的那些次壳层中的电子——这 些壳层称为磁性电子壳层。 对于多电子系统: B l L(L 1) ml L

二、电子自旋磁矩 实验证明:电子自旋磁矩在外磁场方向分量等于一个4B,取正或取负。 血,a=g=±功=士 eh e h 2m m 2 自旋角动量: Ps=S(S+1)h 在外场方的分量代)=mA=士号 (白旋磁量子数:m=±) ·.自旋磁矩与自旋角动量的关系为: a)n=-e便a 方向相反瓜=-CP=一yP
二、电子自旋磁矩 实验证明:电子自旋磁矩在外磁场方向分量等于一个μB,取正或取负。 s s H s H s s H s S H B m e m e m m S S m e m e μ P P μ P P P μ μ s s s s 方向相反 =- =- 自旋磁矩与自旋角动量的关系为: (自旋磁量子数: 在外场方向分量: 自旋角动量: ) 2 1 2 1 2 2

其中:y=e,为自旋磁力比,且:y,=2, m 4,的绝对值: H=JS(S+1)eh=21S(S+1)un S=>ms 1.总自旋磁矩在外场方向的分量为: (s)H=2m,4B,m,=±1/2,最大分量:[s)H]max=2S4B 2.计算原子总自旋角动量时,只考虑未填满次壳层中 的电子。 3.电子总磁矩可写为: a-司2n=次81nac因于 g=1,来源于轨道运动; g=2,来源于自旋; 1<8<2,来源于二者
s B s s s l S S m e S S m e 1 2 1 , : 2 的绝对值: 其中: 为自旋磁力比,且 1. 总自旋磁矩在外场方向的分量为: 2. 计算原子总自旋角动量时,只考虑未填满次壳层中 的电子。 3. 电子总磁矩可写为: H ms B ms H 2S B μs =2 , 1/ 2,最大分量:[ μs ]max 来源于二者 , 来源于自旋; , 来源于轨道运动; , 因子 1 2, 2 g 1 : Lande 2 g g P P g m e g mS S