
第2章平面波简述-目录 电子科技大学计算电磁学及其应用团队,CEMLAB /058 2.1波动方程与平面波 2.2平面波的极化 2.3波的本征常数 2.4损耗介质中的平面波 2.5平面波的反射 2.6传输线概念 2.7矩形波导概述 2.8矩形谐振腔概述 2.9自由空间辐射问题概述 2
2 电子科技大学计算电磁学及其应用团队,CEMLAB 2 第2章 平面波简述-目录 2.1 波动方程与平面波 2.2 平面波的极化 2.3 波的本征常数 2.4 损耗介质中的平面波 2.7 矩形波导概述 2.8 矩形谐振腔概述 2.9 自由空间辐射问题概述 2.5 平面波的反射 2.6 传输线概念

3 电子科技大学计算电磁学及其应用团队,CEMLAB 1958 什么叫波动方程? 电磁场的波动方程是如何得出来的? 什么叫(均匀)平面波?
3 电子科技大学计算电磁学及其应用团队,CEMLAB 什么叫波动方程? 电磁场的波动方程是如何得出来的? 什么叫(均匀)平面波?

电子科技大学计算电磁学及其应用团队,CEMLAB ab 1958 一般的标量波动方程(关于时间和空间的二阶偏微分方程): 被兼传操方向 三维波动方程 =f(x,y,) 高H 三维齐次波动方程 +*-0 其解为u=ejore (波函数) u 1 8u 一 维波动方程 012 v2 0x2 =f(x,0 u 1 u 一维齐次波动方程 =0 其解为u=elole (一维波函数) 0t2v20x2
电子科技大学计算电磁学及其应用团队,CEMLAB 一般的标量波动方程(关于时间和空间的二阶偏微分方程): 2 222 22 2 2 2 1 ,,, u uuu f xyzt tvx y z 2 2 2 22 1 , u u f x t t vx 2 2 2 22 1 0 u u t vx 三维波动方程 一维波动方程 一维齐次波动方程 j t jkx uee 其解为 2 222 22 2 2 2 1 0 u uuu tvx y z 三维齐次波动方程 j t jk r uee 其解为 (波函数) (一维波函数)

电子科技大学计算电磁学及其应用团队,CEMLAB ab /95a 平面波 柱面波 球面波 ● ⊙ 25
电子科技大学计算电磁学及其应用团队,CEMLAB -5 -2.5 0 2.5 5 -5 -2.5 0 2.5 5 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 -5 -2.5 0 2.5 5 -5 -2.5 0 2.5 5 -0.4 -0.2 0 0.2 0.4 0.6 0.8 x/ z/ -5 -2.5 0 2.5 5 -5 -2.5 0 2.5 5 -0.2 0 0.2 0.4 0.6 0.8 1 平面波 柱面波 球面波

2.1波动方程与平面波 电子科技大学计算电磁学及其应用团队,CEMLAB 6 /95a 2.1.1波动方程 研究空间中电磁波的传播特性,仅需求解齐次Helmholtz方程 E+k2E=0 VH+kH=0 其中k=o√e称为传播常数,上述方程也称为矢量波动方程。 直角坐标系下,每一个电场和磁场分量都满足标量波动方程 Vw+kv=0 (v=E.EE.H.Hy.H.) 假设电场只有x分量且与x和y坐标无关,即E=u,E,(z), 电场的波动方 程化为 dE:+KE,=0 6
6 电子科技大学计算电磁学及其应用团队,CEMLAB 6 2.1 波动方程与平面波 研究空间中电磁波的传播特性,仅需求解齐次Helmholtz方程 直角坐标系下,每一个电场和磁场分量都满足标量波动方程 2 2 E kE 0 2 2 H kH 0 其中 称为传播常数,上述方程也称为矢量波动方程。 k 2 2 0 ,, , , x yz x y z k EEE HHH 或 假设电场只有 x分量且与 x 和y坐标无关,即 ,电场的波动方 程化为 ˆ E uE z x x 2 2 2 0 x x d E k E dz 2.1.1 波动方程

2.1波动方程与平面波 电子科技大学计算电磁学及其应用团队,CEMLAB 1958 其解为E,=Ee(+z方向的行波),等相位面为-kz=C(z为常数即为 平面波)。代入Maxwell7方程得 H: 定义波阻抗1= 注意:波阻抗是与波的传播方向有关的,一般(E.H、构成右手螺旋法则(k指 波的传播方向,飞=E×庄,A表示沿矢量方向的单位矢量)若违背右手螺旋法 则,则波阻抗需要带负号。 E H. H 7
7 电子科技大学计算电磁学及其应用团队,CEMLAB 7 定义波阻抗 x y E H 其解为 ( +z方向的行波),等相位面为 -kz = C ( z为常数即为 平面波)。代入Maxwell方程得 0 jkz E x E e H E y x 2.1 波动方程与平面波

2.1波动方程与平面波 8 电子科技大学计算电磁学及其应用团队,CEMLAB 例如上述一维波动方程,若取-z方向行波解E,=E。e,代入Maxwell方程得 Hy Ex 于是n=H, 右手螺旋的顺序: 直角坐标(x,y,z),(y,z,x),(z,x,y), 圆柱坐标(p,p,z),(p,Z,p),(z,P,0), 球坐标(r,0,0),(0,p,),(p,I,日), 若是上述任意两个变量调换顺序,则不满足右手螺旋法则 举例:乙=,乙,=- Ee H志 Ho (0,0,r)违背右手螺旋,故为负号 自由空间波阻抗0= 0=120m=377 8
8 电子科技大学计算电磁学及其应用团队,CEMLAB 8 若是上述任意两个变量调换顺序,则不满足右手螺旋法则 2.1 波动方程与平面波
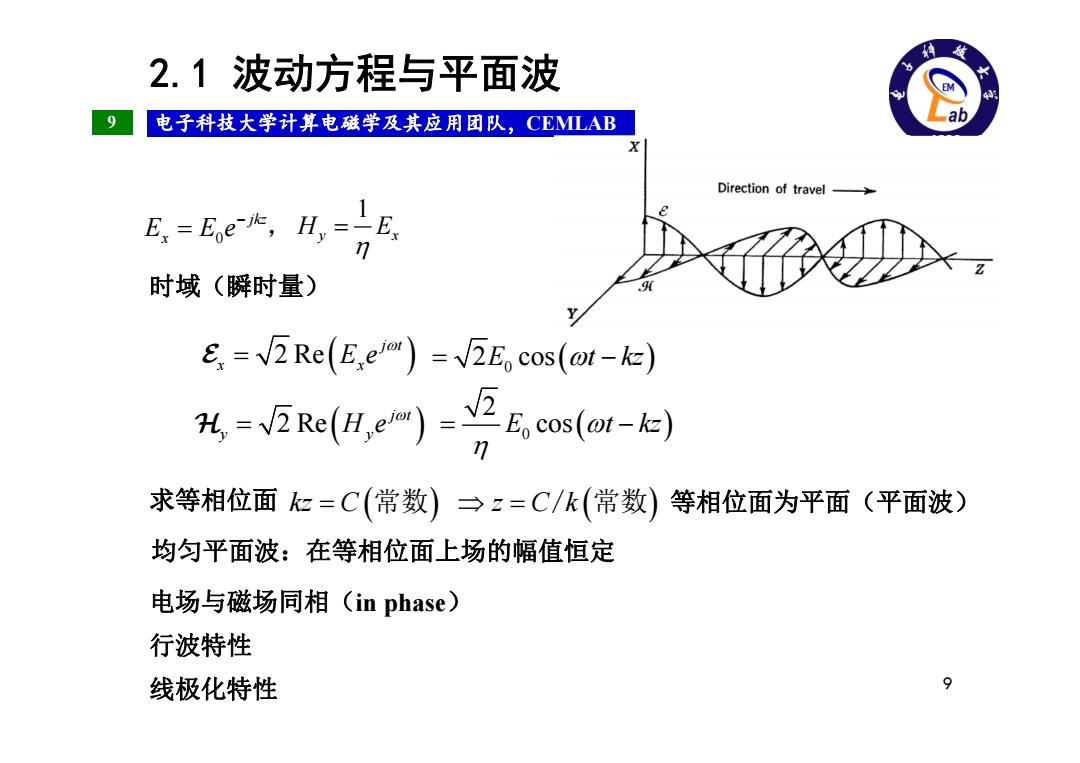
2.1波动方程与平面波 电子科技大学计算电磁学及其应用团队,CEMLAB Lab Direction of travel B,=Ee-k,H,=E 时域(瞬时量) E,=V2Rc(E,em)=V2E.cos(@t-k-) H=万Rc(H,e)-5 .co(o-) 求等相位面亿=C(常数)→z=C/k(常数) 等相位面为平面(平面波) 均匀平面波:在等相位面上场的幅值恒定 电场与磁场同相(in phase) 行波特性 线极化特性 9
9 电子科技大学计算电磁学及其应用团队,CEMLAB 9 时域(瞬时量) 0 jkz E Ee x , 1 H E y x 2 Re j t x x E e 2 cos E0 t kz 2 Re j t y y H e 0 2 E cos t kz 求等相位面 kz C 常数 z Ck/ 常 数 等相位面为平面(平面波) 均匀平面波:在等相位面上场的幅值恒定 电场与磁场同相(in phase ) 行波特性 线极化特性 2.1 波动方程与平面波
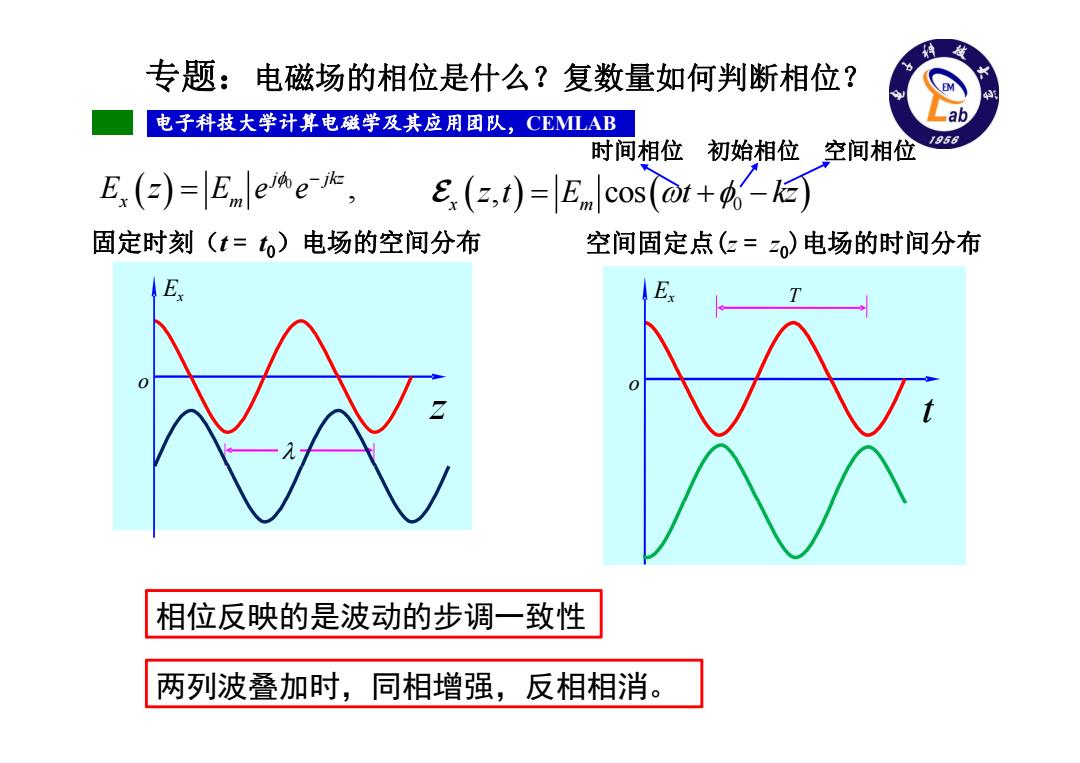
专题:电磁场的相位是什么?复数量如何判断相位? 电子科技大学计算电磁学及其应用团队,CEMLAB 6 时间相位 初始相位 空间相位 E(=)=Eee, E(z,t)=|E,ncos©t+ 固定时刻(t=to)电场的空间分布 空间固定点(2=)电场的时间分布 相位反映的是波动的步调一致性 两列波叠加时,同相增强,反相相消
电子科技大学计算电磁学及其应用团队,CEMLAB 专题:电磁场的相位是什么?复数量如何判断相位? 0 , j jkz E z Eee x m x m z t E t kz , cos 0 o Ex z 固定时刻(t = t0)电场的空间分布 两列波叠加时,同相增强,反相相消。 时间相位 初始相位 空间相位 相位反映的是波动的步调一致性 t T o Ex 空间固定点(z = z 0)电场的时间分布

电子科技大学计算电磁学及其应用团队,CEMLAB ab 1956 复数形式的场如何计算相位? 复数的一般形式Ae Im↑ 皮a+乃则m-会 1+j π 4 例 E(z)=Ee Re 3π -1j 中=- 4 H(=)=e 西 复平面分析方法 E,(z)和H,(z)相位相差多少?
电子科技大学计算电磁学及其应用团队,CEMLAB 复数形式的场如何计算相位? 复平面分析方法 Re Im 4 1 j 3 - 4 -1-j j 复数的一般形式 A e tan b a a jb 则 例 jkz E x m z Ee 0 0 jkz m y jE e H z Ez Hz x y 和 相位相差多少? 或