
第二章静电场 Electrostatic field 1
第二章 静电场 Electrostatic field 1

本章研究的主要问题是:在给定的自由电荷分布 以及周围空间介质和导体分布的情况下,如何求解电 场。 注意两点:①电荷静止,即:=O ②电场不随时间变化,即: Ot 本章求解静电场的方法有:①分离变量法;②镜 像法;③格林函数法。 求解的依据是:唯一性定理。 2
本章研究的主要问题是:在给定的自由电荷分布 以及周围空间介质和导体分布的情况下,如何求解电 场。 注意两点:①电荷静止,即: ②电场不随时间变化,即: 本章求解静电场的方法有:①分离变量法;②镜 像法;③格林函数法。 求解的依据是:唯一性定理。 v 0 0 t E 2

本章主要内容 静电场的标势及其微分方程 唯一性定理 拉普拉斯方程,分离变量法 镜象法 格林函数法 电多极矩 3
本 章 主 要 内 容 静电场的标势及其微分方程 唯一性定理 拉普拉斯方程,分离变量法 镜象法 格林函数法 电多极矩 3

§2.1静电场的标势及其微分方程 Scalar potential and differential equation for electrostatic field
§2.1 静电场的标势及其微分方程 Scalar potential and differential equation for electrostatic field 4

1.静电场的标势和微分方程 静电现象满足以下两个条件:即①电荷静止不 动;②场量不随时间变化。故 j=pv=0; (物理量)=0 8t 把静电条件代入Maxwell's equations中去,即得电场 满足的方程 V×E=0 Y.D=p
1.静电场的标势和微分方程 静电现象满足以下两个条件:即 ①电荷静止不 动;②场量不随时间变化。故 把静电条件代入Maxwell's equations中去,即得电场 满足的方程 0 ; ( ) 0 物理量 t j D E 0 5

这两方程连同介质的电磁性质方程刀=是解决静 电问题的基础 根据电场方程V×E=0(即E的无旋性),可引 入一个标势0。 在电磁学中,已知o()-o(B)=-E:d团因为相 距为d两点的电势差为 do =-E.dl 由于dg= o0 dy*o dxoy 0o dz-o.dl Ox 所以 E=-Vo 6
这两方程连同介质的电磁性质方程 是解决静 电问题的基础。 根据电场方程 (即 的无旋性),可引 入一个标势 。 在电磁学中,已知 因为相 距为 两点的电势差为 由于 所以 D E E 0 A B A B E dl ( ) ( ) dl d E dl dz dl z dy y dx x d E E 6

又因为在均匀各向同性的介质中,D=E则有 V.D=V.(E)=VE.E+8V.E =P 这里Ve=0,故有 Y.D=8V.E-8V.(-Vp)=p 即 V20 三 P E 此方程称为泊松方程(Poisson equation, 若在无源区域内(p=O),上式化为 Vp=0 7
又因为在均匀各向同性的介质中, 则有 这里 ,故有 即 此方程称为泊松方程(Poisson equation). 若在无源区域内( ),上式化为 D E D E E E ( ) 0 D E () 2 0 2 0 7

此方程称为拉普拉斯方程(Laplace equation) 在各种不同条件下求解Poisson equation:或 Laplace equation是处理静电问题的基本途径。 2、静电场的基本问题 如果电荷是连续分布的,则观察点处的标势为 这个式子只反映了电荷激发电场这一面,而没有反 映电场对电荷的作用另一面。 如果空间还有导体存在的活,那么物理机制为
此方程称为拉普拉斯方程(Laplace equation) 在各种不同条件下求解Poisson equation或 Laplace equation是处理静电问题的基本途径。 2、静电场的基本问题 如果电荷是连续分布的,则观察点 处的标势为 这个式子只反映了电荷激发电场这一面,而没有反 映电场对电荷的作用另一面。 如果空间还有导体存在的活,那么物理机制为 x V d r x x ( ) 4 1 ( ) 0 8
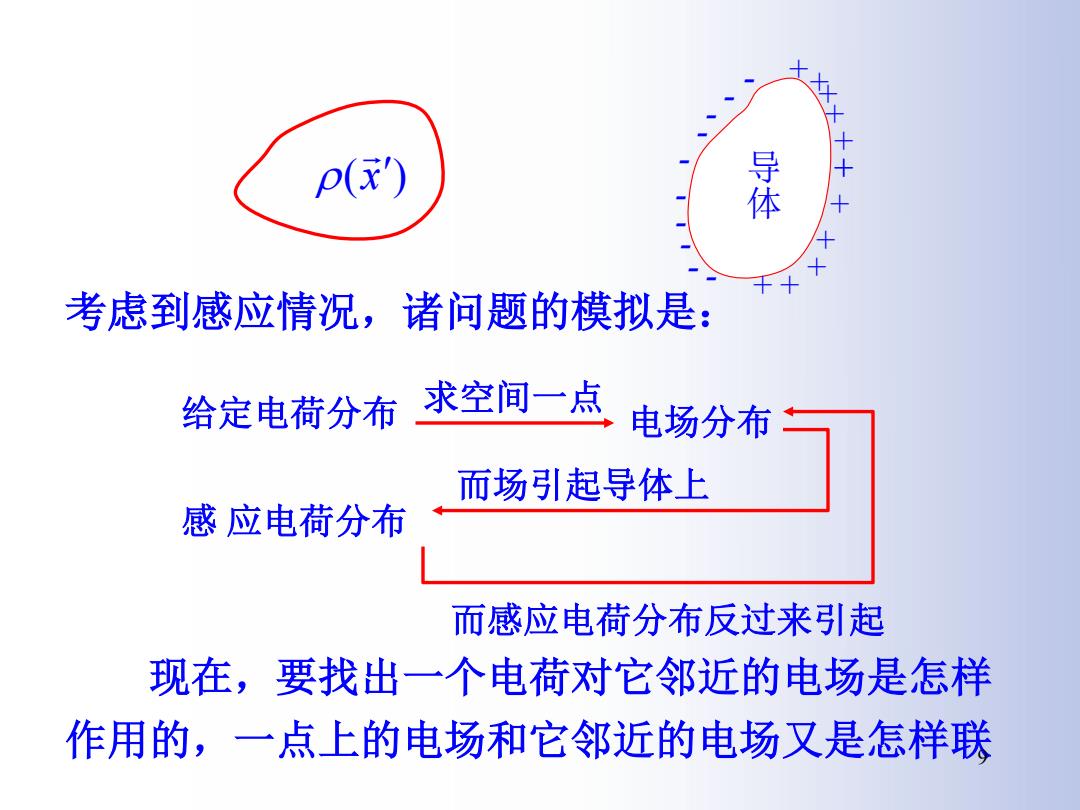
p(') 瀑 考虑到感应情况,诸问题的模拟是: 给定电荷分布 求空间一点 电场分布 而场引起导体上 感应电荷分布 而感应电荷分布反过来引起 现在,要找出一个电荷对它邻近的电场是怎样 作用的,一点上的电场和它邻近的电场又是怎样联
考虑到感应情况,诸问题的模拟是: 现在,要找出一个电荷对它邻近的电场是怎样 作用的,一点上的电场和它邻近的电场又是怎样联 (x ) 导 体 + + + + + + + ++ + - + - - - - - - - - - 给定电荷分布 求空间一点 电场分布 而场引起导体上 感 应电荷分布 而感应电荷分布反过来引起 9

系的,即要找出电荷和电场相互作用规律的微分形 式,而在导体表面或其他边界上场和电荷的相互作 用关系侧由边值关系和边界条件反映出来,称之为 边值问题。 (1)在介质的分界面上,电场满足的边值关系 为 方×(E2-E)=0 (D,-D)=p 且为电势所满足的边值关系: 10
系的,即要找出电荷和电场相互作用规律的微分形 式,而在导体表面或其他边界上场和电荷的相互作 用关系则由边值关系和边界条件反映出来,称之为 边值问题。 (1)在介质的分界面上,电场满足的边值关系 为 且为电势所满足的边值关系: ( ) ˆ ( ) 0 ˆ 2 1 2 1 n D D n E E 10