
计算电罐学实验室Computational Electromagnetics Laboratory 966 计算电磁学 园书 电子科技大学邵维 2020年4月 1
1 计算电磁学 电子科技大学 邵维 2020年4月 计算电磁学实验室 Computational Electromagnetics Laboratory
计算电磁学 (小班研讨课) 966 目录 课程基础 第8章矩量法基本原理 2
2 计算电磁学(小班研讨课) 目 录 课程基础 第8章 矩量法基本原理
课程基础 966 ▣ 计算机硬件决定了计算电磁学的发展,计算电磁学推动了电磁场工程的发展 一个简单的例子:解析法一近似法 —数值法 同轴线 含金属通孔 微带线 的微带线 Q1:同轴线中的电场分别可由电位函数导出,位函数满足什么方程?如何求解? Q2:微带线中传播的主模是什么?主模有什么特点?是否能用严格解析法求解? 4
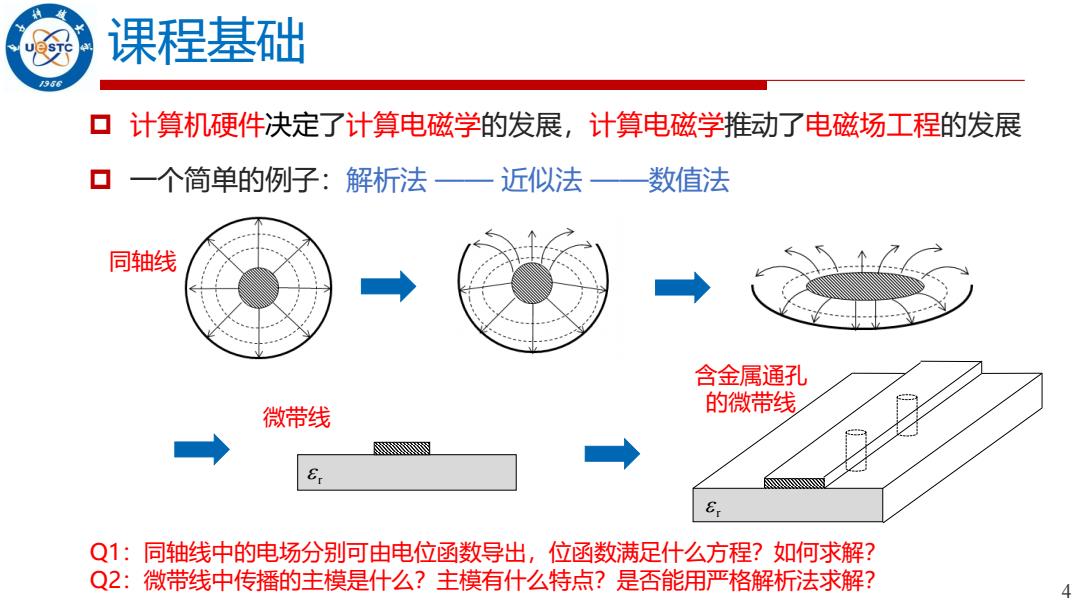
4 课程基础 计算机硬件决定了计算电磁学的发展,计算电磁学推动了电磁场工程的发展 一个简单的例子:解析法 —— 近似法 ——数值法 Q1:同轴线中的电场分别可由电位函数导出,位函数满足什么方程?如何求解? Q2:微带线中传播的主模是什么?主模有什么特点?是否能用严格解析法求解? r 微带线 r 含金属通孔 的微带线 同轴线
课程基础 966 ▣ 数值方法分类 时域 FDTD、FETD Q1:FDTD的优点有哪些? 基于微分方程 Q2:学习FDFD后,你认为它在 频域 FDFD、FEM 数值计算中应用很少的原因 时域 是什么? IETD 基于积分方程 频域 MoM、FMM ▣数值方法和高频近似方法 高频近似方法 数值方法 0.1 10入 100元 10002 物体电尺寸 Q3:数值方法和高频近似方法在实施过程中的显著区分是什么? 5
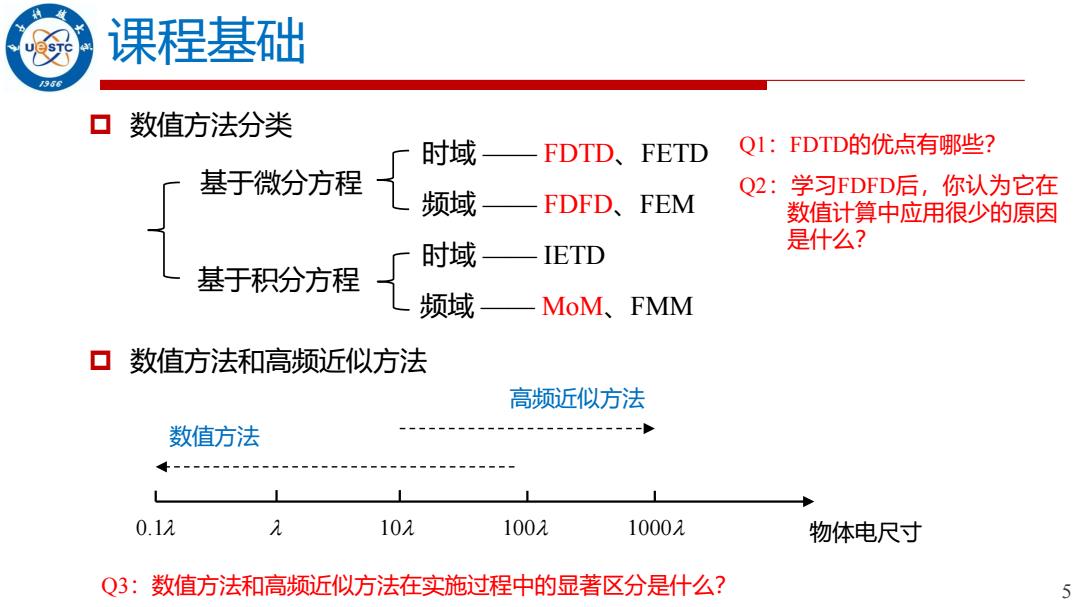
5 课程基础 数值方法分类 基于积分方程 基于微分方程 时域 —— IETD 频域 —— MoM、FMM 时域 —— FDTD、FETD 频域 —— FDFD、FEM 0.1 10 100 1000 物体电尺寸 数值方法 高频近似方法 数值方法和高频近似方法 Q3:数值方法和高频近似方法在实施过程中的显著区分是什么? Q1:FDTD的优点有哪些? Q2:学习FDFD后,你认为它在 数值计算中应用很少的原因 是什么?
课程基础 956 矩量法 (method of moments,MoM) 名称的由来 >数学中,∫xf(x)dr称为函数的n阶矩 矩量法中,用权函数替代x” >电磁学中,即求解积分方程的方法 口MoM和FDTD求解单极天线的不同 ABC 求解E、H 求解1 FDTD MoM 激励 激励 6
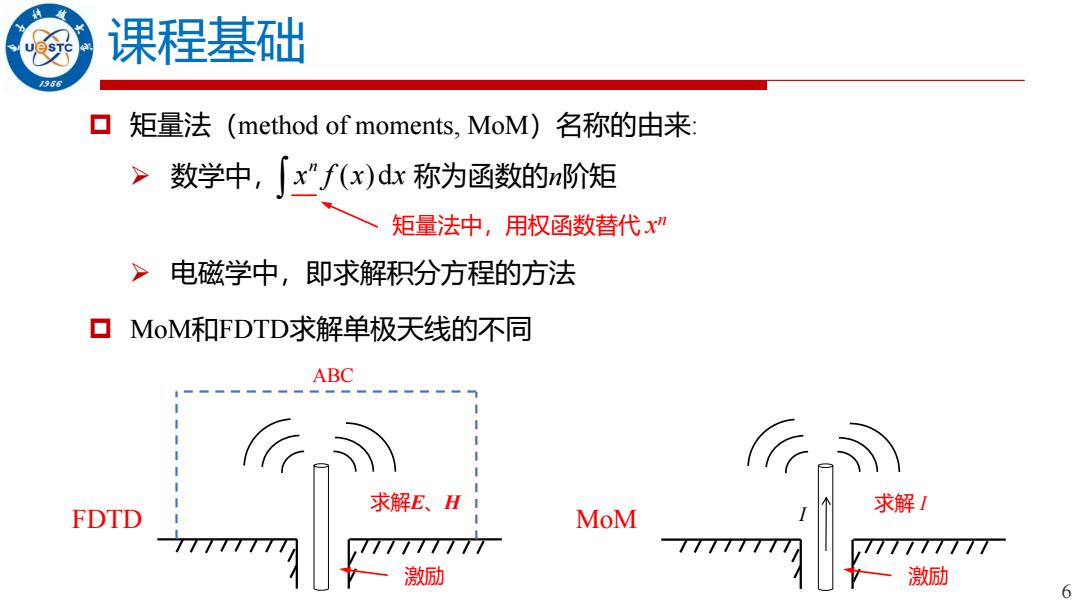
6 课程基础 矩量法(method of moments, MoM)名称的由来: ➢ 数学中, 称为函数的n阶矩 矩量法中,用权函数替代 x n ➢ 电磁学中,即求解积分方程的方法 ( )d n x f x x MoM和FDTD求解单极天线的不同 FDTD 激励 求解E、H MoM 激励 求解 I ABC I
课程基础 966 FDTD、MoM和FEM的比较 FDTD FEM MoM 任意两个未知数 1.通过一系列中间变量间接表述 L.通过格林函数直接表述 的相互作用 2.存在色散误差 2.不存在色散误差 方程性态 差 好 截断边界 需要施加ABC 无需施加ABC 实施难度 易 居中 难 通用性 强 强+ 弱 精度 低 居中 高 Q1:FDTD法中的任意两个未知变量是如何间接表述的? Q2:影响FDTD精度的因素有哪些? MoM:主要用于求解天线辐射和目标散射问题 > 1963年,K.K.Mei(梅冠香),博士论文 >1 968年,R.F.Harrington,专著 7
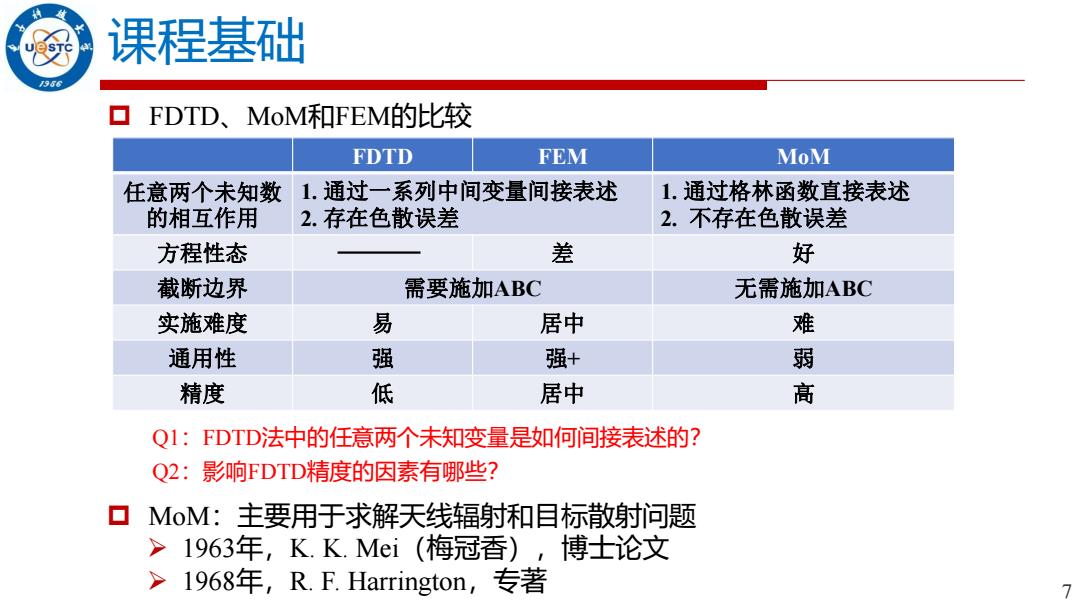
7 课程基础 FDTD FEM MoM 任意两个未知数 的相互作用 1. 通过一系列中间变量间接表述 2. 存在色散误差 1. 通过格林函数直接表述 2. 不存在色散误差 方程性态 差 好 截断边界 需要施加ABC 无需施加ABC 实施难度 易 居中 难 通用性 强 强+ 弱 精度 低 居中 高 FDTD、MoM和FEM的比较 Q1:FDTD法中的任意两个未知变量是如何间接表述的? Q2:影响FDTD精度的因素有哪些? MoM:主要用于求解天线辐射和目标散射问题 ➢ 1963年,K. K. Mei(梅冠香),博士论文 ➢ 1968年,R. F. Harrington,专著

8.1矩量法原理 966 8.1.1矩量法基本概念 >非齐次方程 L(0=8 (1) 其中,L是线性算子,g为已知函数,f为未知函数。电磁场问题中,L是 积分或微分算子,g是激励源或入射场,f是待求的电荷或电流。 Q1:什么是线性算子? Q2:单从方程的形式看,求解方程(1)的困难是什么? >令f展开为N个基函数的组合 f≈∑anf 3) 其中,4是系数,f为基函数。(2)代入(1)中,再利用算子的线性,得
9 8.1 矩量法原理 8.1.1 矩量法基本概念 ➢ 非齐次方程 L(f) = g (1) 其中,L是线性算子,g为已知函数,f 为未知函数。电磁场问题中,L是 积分或微分算子,g是激励源或入射场,f 是待求的电荷或电流。 Q1:什么是线性算子? Q2:单从方程的形式看,求解方程(1)的困难是什么? ➢ 令 f 展开为N个基函数的组合 (2) 其中,an 是系数,fn为基函数。(2)代入(1)中,再利用算子的线性,得 1 N n n n f a f =

8.1矩量法原理 1966 之aL9一e,提福集:内存有限,w为有明 这里,余量 R=g-2a,L(/) 为保证最小,应令余量加权求积后取零值,即取一权函数(检验函数、试 探函数)的集合{w},令 a8-2a1=0m=12N (3) 其中,内积的定义 (fn,fn〉=.f.fd 10
10 这里,余量 为保证R最小,应令余量加权求积后取零值,即取一权函数(检验函数、试 探函数)的集合{w},令 (3) 其中,内积的定义 ( ) 1 N n n n a L f g = N→∞,{ f }是一完备集;内存有限,N为有限值 ( ) 1 N n n n R g a L f = = − ( ) 1 , 0, 1,2,..., N m n n n g a L f m N = − = = , d m n m n V f f f f V = 8.1 矩量法原理

8.1矩量法原理 1966 (3)由n个方程组成的方程组; (3)表示因不能精确满足场方程而导致的误差在平均意义下等于零; (3)意味着余量R为wn取矩的一组平衡式;数学上,∫x”f(x)dx称为函数f 的阶矩,这里用代替x”,故称为矩量法。 由(3)得 立aaL》=o,8 产生的矩阵为N×N,即Za=b,其中 Znm=(om,L(fn)》 每一个基函数通过格林函数和其他所有 基函数发生作用,产生的矩阵为满阵 bm=(0n,g〉 11
11 ➢ (3)由n个方程组成的方程组; ➢ (3)表示因不能精确满足场方程而导致的误差在平均意义下等于零; ➢ (3)意味着余量 R 为 wm取矩的一组平衡式;数学上, 称为函数 f 的n阶矩,这里用代替x n ,故称为矩量法。 ( )d n x f x x 由(3)得 产生的矩阵为N×N,即 Za = b,其中 , ( ) Z L f mn m n = , m m b g = ( ) 1 , , N n m n m n a L f g = = 每一个基函数通过格林函数和其他所有 基函数发生作用,产生的矩阵为满阵 8.1 矩量法原理

8.1矩量法原理 966 8.1.2矩量法中的权函数 一点匹配 如果边界条件是通过物体上一系列离散点而施加上的,等效于 onm(r=δ(r 优点:实施易 一不需计算作用在权函数上的积分。 Q:为什么? A:[f(x)6(x-xo)dx=f(xo) 缺点:精度差一边界条件只在离散点处匹配,解域内其他点存在误差。 12
12 8.1.2 矩量法中的权函数 一 点匹配 如果边界条件是通过物体上一系列离散点而施加上的,等效于 优点:实施易——不需计算作用在权函数上的积分。 Q:为什么? 缺点:精度差——边界条件只在离散点处匹配,解域内其他点存在误差。 m (r r ) = ( ) 0 0 f x x x x f x ( ) ( )d ( ) − − = A: 8.1 矩量法原理