
计算电磁学 (小班研讨课) 966 录 第十章积分方程 目 2
2 计算电磁学(小班研讨课) 目 录 第十章 积分方程

10.4细导线的线积分方程 966 场点 10.4.1细线近似 源点 a a<<L→细线→开放结构→EFIE J(r)=- : J与方位角p无关, 2 2πa 并在两端为零 圆柱坐标系下,磁矢量位A可由表面积分得到 d dl'=ado' IP-P' aor do' 余弦定理 r=Ir-r1=y--z)+l-pT lp-pf=pita-2p-p 该式是(0'-p)的函数,结果轴对称 =p2+a2-2pac0s(p'-p)) 用p'替代(p'-p) 3
3 2a z 2 L 2 L − o r ' r z z − ' ρ − ρ ' 10.4.1 细线近似 10.4 细导线的线积分方程 a << L → 细线 → 开放结构 → EFIE ( ) ( ) ˆ 2 z I z a J r z = J与方位角φ无关, 并在两端为零 圆柱坐标系下,磁矢量位Az可由表面积分得到 ( ) ( ) j 2 2 0 2 ' e , , d 'd ' 2 4 L kr z z L I z A z z r − − = d𝜑’ 𝑎 dl’ d '= d ' l a ( ) 2 2 r z z = − = − + − r r' ' ' ρ ρ ρ − ρ ' ρ ' ρ '− 余弦定理 ( ) 2 2 2 2 2 ' 2 ' 2 cos ' a a a − = + − = + − − ρ ρ ρ ρ a 该式是( '− ) 的函数,结果轴对称 用 ' 替代 ( '− ) 源点 场点
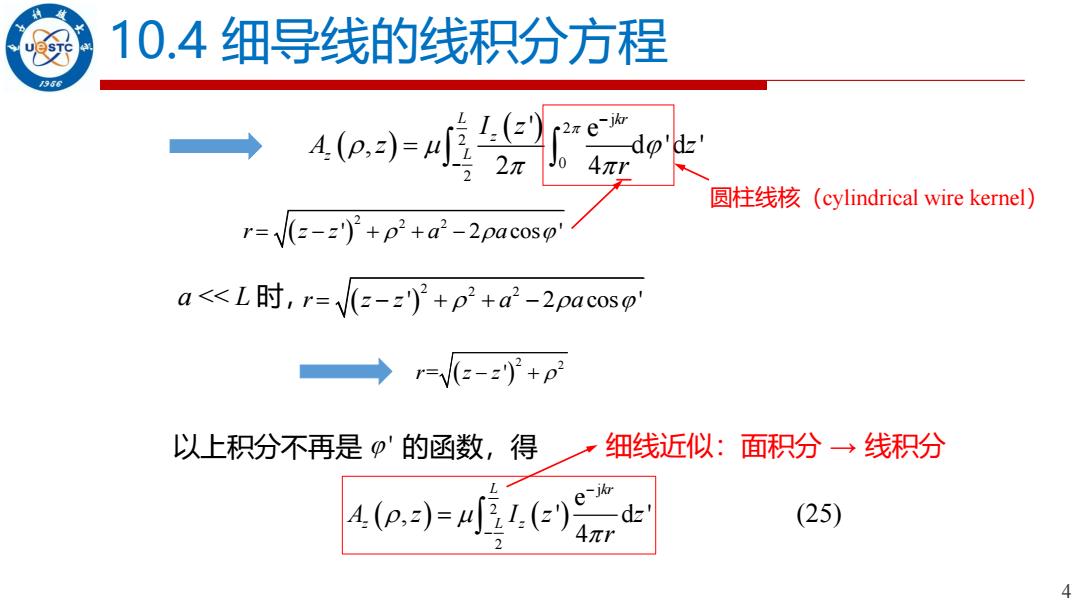
10.4细导线的线积分方程 966 A(p,)= 人空x三 do'dz' 2元 4πr 圆柱线核(cylindrical wire kernel) r=/(=-:)'+p+a-2pacoso" a<L时,r=V(z-z2+p2+a2-2 pacos ◆ r=v(E-=)+e 以上积分不再是'的函数,得 细线近似:面积分→线积分 4(D)=1,(e (25) 4
4 10.4 细导线的线积分方程 ( ) ( ) j 2 2 0 2 ' e , d 'd ' 2 4 L kr z z L I z A z z r − − = ( ) 2 2 2 r z z a a = − + + − ' 2 cos ' 圆柱线核(cylindrical wire kernel) a << L 时, ( ) 2 2 2 r z z a a = − + + − ' 2 cos ' ( ) 2 2 r z z = ' − + 以上积分不再是 ' 的函数,得 ( ) ( ) j 2 2 e , ' d ' 4 L kr A z I z z z z L r − − = (25) 细线近似:面积分 → 线积分

10.4细导线的线积分方程 9656 由式(15)E=-j0A-」V(·A)的标量场形式: @LE E=-joA-jo (26) 未知 未知 未知 通过线表面的切向场边界条件,得到关于入射场E的细线EFIE Ei=- (27) 思考:从(26)推导出(27 ⊙IE 其中,r=-z)2+a。 电流只在线的表面流动,但由于导线很细,表 面电流可等效为位于轴上线电流的作用 注意:这里由p变成了a 5
5 10.4 细导线的线积分方程 通过线表面的切向场边界条件,得到关于入射场 Ei 的细线EFIE 2 i 2 2 j E k A z z z = + (27) ( ) 2 2 其中, r z z a = − + ' 。 电流只在线的表面流动,但由于导线很细,表 面电流可等效为位于z轴上线电流的作用 思考:从(26)推导出(27) 注意:这里由 ρ 变成了a ( ) j j 由式(15) E A A = − − 的标量场形式: 2 s 2 j j E A A z z z z = − − 未知 未知 未知 (26)
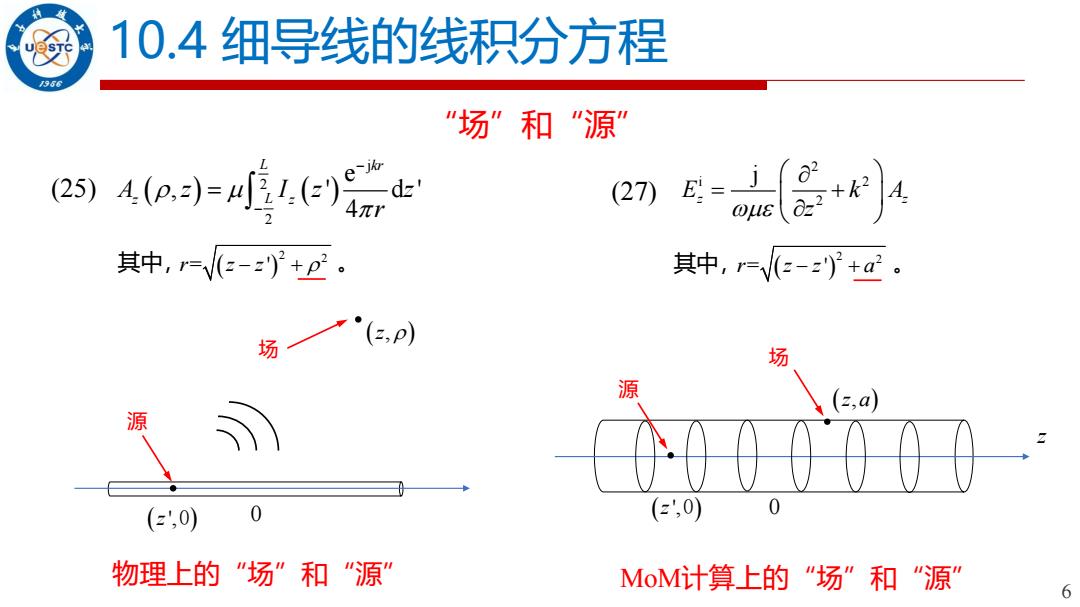
10.4细导线的线积分方程 966 “场”和“源 25)Ao=j值L(e)rd止 (27) E:=-J6 其中,=-+p2。 其中,=e-+a2。 场 (a,p) 场 源 (z,a 源 (',0) 0 (z',0) 物理上的“场”和“源” MoM计算上的"场”和“源" 6
6 10.4 细导线的线积分方程 “场”和“源” ( ) ( ) j 2 2 e , ' d ' 4 L kr A z I z z z z L r − − = (25) ( ) 2 2 其中, r z z = ' − + 。 (27) 2 i 2 2 j E k A z z z = + ( ) 2 2 其中, r z z a = ' − + 。 0 z (z',0) 源 (z, ) 场 物理上的“场”和“源” MoM计算上的“场”和“源” 源 (z',0) 场 0 (z a, )

10.4细导线的线积分方程 1966 两个著名的求解细线的基本方程 当微分算子在积分符号外,可得到Hallen积分方程 (28) 当微分算子在积分符号内,可得到Pocklington积分方程 e dz (29) 4πr Q:从方程形式上看,哪一个方程MoM求解更困难?为什么? 7
7 10.4 细导线的线积分方程 当微分算子在积分符号外,可得到Hallen积分方程 ( ) ( ) 2 j i 2 2 2 2 j e ' d ' 4 L kr E z k I z z z z L z r − − = + 两个著名的求解细线的基本方程 当微分算子在积分符号内,可得到Pocklington积分方程 ( ) ( ) 2 j i 2 2 2 2 j e ' d ' 4 L kr E z I z k z z z L z r − − = + (28) (29) Q:从方程形式上看,哪一个方程MoM求解更困难?为什么?
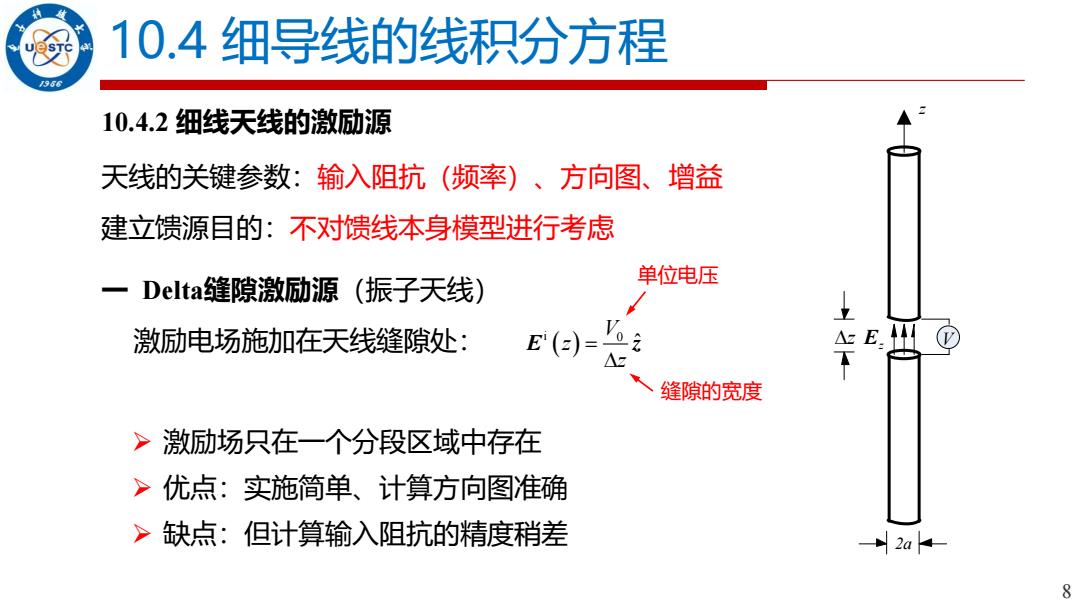
10.4细导线的线积分方程 1966 10.4.2细线天线的激励源 天线的关键参数:输入阻抗(频率)、方向图、增益 建立馈源目的:不对馈线本身模型进行考虑 Delta:缝隙激励源(振子天线) 单位电压 激励电场施加在天线缝隙处: 2 E(e)= △zE △z 缝隙的宽度 >激励场只在一个分段区域中存在 >优点:实施简单、计算方向图准确 >缺点:但计算输入阻抗的精度稍差 2a 8
8 10.4 细导线的线积分方程 10.4.2 细线天线的激励源 一 Delta缝隙激励源(振子天线) z 2a E z z V 天线的关键参数:输入阻抗(频率)、方向图、增益 建立馈源目的:不对馈线本身模型进行考虑 激励电场施加在天线缝隙处: ( ) i 0 ˆ V z z = E z 单位电压 缝隙的宽度 ➢ 激励场只在一个分段区域中存在 ➢ 优点:实施简单、计算方向图准确 ➢ 缺点:但计算输入阻抗的精度稍差

10.4细导线的线积分方程 966 二磁流环激励源 (单极子天线) ↑: 2a 2a 口径面TEM波: E(p)-2pln(b/a 由镜像原理,用磁流环替代地平面和口径面, 得到等效磁流密度: M(p)=-2ixE(p) -1 pin(bla. a≤p≤b -2b 同轴馈电 磁流环 E(p) EP Q: 为什么将“同轴馈电模式” 镜像原理 转换为“磁流环模式”? 等效原理 边界条件 0→∞ -E(p)· M.=-nx(E(p)-(-E(P)))
9 10.4 细导线的线积分方程 二 磁流环激励源(单极子天线) z 2a 2b E z 2a M 同轴馈电 磁流环 口径面TEM波: ( ) ( ) 1 ˆ 2 ln / b a E = ρ 由镜像原理,用磁流环替代地平面和口径面, 得到等效磁流密度: ( ) ( ) ( ) 2 ˆ 1 ˆ, ln / a b b a = − − = M n E φ Q:为什么将“同轴馈电模式” 转换为“磁流环模式”? σ→∞ E ( ) M n E E s = − − − ( ( ) ( ( ))) E ( ) -E ( ) 镜像原理 n 边界条件 𝑴s

10.4细导线的线积分方程 966 磁流产生一个沿向的电场。对于磁流环中心(p=0),电场为 E()= 2In(b/a) 22+a2 V22+b 上式得到的向电场可作为一个激励场源。 300 250 150 电场沿方向快速衰减 100 50 8.7 -0.05 0 0.05 0.1 Position(m) 10
10 10.4 细导线的线积分方程 磁流产生一个沿z向的电场。对于磁流环中心( = 0 ),电场为 ( ) ( ) 2 2 2 2 j j i 2 2 2 2 1 e e 2ln / k z a k z b E z z b a z a z b − + − + = − + + 上式得到的z向电场可作为一个激励场源。 电场沿z方向快速衰减

10.3表面积分方程 966 三平面波激励源 对细导线,入射电场E的切向分量表示为 En(r)=i(r).E(r) 单位切向矢量 入射电场E的入射角度为0,幅度为归一化,有 k Eam(r)=sin0eika 入射角0 =Sin geikcose k在z上的投影 细导线上只有分量的电流,没有分量的电流,所以极化的入射波不 会在天线上产生感应电流 11
11 10.3 表面积分方程 三 平面波激励源 z i E k 对细导线,入射电场 Ei 的切向分量表示为 ( ) ( ) ( ) i tan E r t r E r = ˆ 单位切向矢量 入射角 入射电场Ei的入射角度为θ,幅度为归一化,有 ( ) j tan j cos sin e sin e kz E = = k z r 细导线上只有z分量的电流,没有φ分量的电流,所以φ极化的入射波不 会在天线上产生感应电流 k 在 z 上的投影