电子科技大学：《计算电磁学 Computational Electronmagentics》课程教学资源（课件讲稿，有限差分法）第2章 有限差分法 2.3 特征值问题（时谐场）的差分计算

计算电磁学（小班研讨课) 966 第2章有限差分法 目录 2.3特征值问题（时谐场)的差分计算 课堂研讨-综合设计（1)-（16) 2

2 计算电磁学（小班研讨课） 目 录 第2章 有限差分法 2.3 特征值问题（时谐场）的差分计算 课堂研讨-综合设计（1）-（16）

计算电磁学 956 第2章有限差分法

3 第2章 有限差分法 计算电磁学

2.3特征值问题（时谐场)的差分计算 966 规则导波系统 直角坐标系下，设导波沿z向传播，传播因子为p(j@t-jz) 1 横向场分量可由纵向场分量表示 J08 .-jB 1 OE. oH. H,=- +jB E=一 OH. -iB E+Jou >k.为截止波数，k2=k2-B2=o2e-B2 4

4 2.3 特征值问题（时谐场）的差分计算  规则导波系统  直角坐标系下，设导波沿z向传播，传播因子为  横向场分量可由纵向场分量表示  为截止波数， 2 c j j z z x E H H k y x               1 2 c j j z z y E H H k x y                1 2 c j j z z x E H E k x y                1 2 c j j z z y E H E k y x                1

2.3特征值问题（时谐场）的差分计算 规则导波系统 纵向场分量满足亥姆霍兹方程：7H2+H2=0 VE2+E2=0 对TE波，E2=0 对TM波，H,=0 金属边界条件 oH. ◆ 对TE波， On 边界=0 (2) x ◆对打M波， E 边界 =0 差分格式：拉普拉斯算子的差分格式 5

5 2.3 特征值问题（时谐场）的差分计算  规则导波系统  纵向场分量满足亥姆霍兹方程：  对TE波，  对TM波，  金属边界条件  对TE波， (?)  对TM波，  差分格式：拉普拉斯算子的差分格式  0   边界 n Hz E z 边界  0 y x

2.3特征值问题（时谐场)的差分计算 数值算例 ◆例1矩形金属波导中的截止波长和场分布 > TE波(Hz)、TM波(Ez) √ 以单标记相应的纵向场分量 在波导内（即场域D)φ满足亥姆霍兹方程 ☑2 +k0=0 少 差分格式 √ 内点g+p2+m+p-40+(kh)=0 波导壁（边界条件） TE波： a =0;0=03； 3 b on c p2+29+p4-4p。+(kh)2p,=0 4 ■ TM波：p,=0 h 网格粗细（△x、△y?） 边界C 6

6 2.3 特征值问题（时谐场）的差分计算  数值算例  例1 矩形金属波导中的截止波长和场分布  TE波（Hz）、TM波（Ez）  以  标记相应的纵向场分量  在波导内（即场域D） 满足亥姆霍兹方程  差分格式  内点  波导壁（边界条件）  TE波： ； ；  TM波：  网格粗细（x、y？） 2 2 2 2 2 =0 c k x y            2 1 2 3 4 0 c 0             4 0 k h 0 n C      1 3    2 2 3 4 c 2 4 0 b b           k h 0 b  2 3 3 0 1 2 4 b 4 h h 1 边界C

2.3特征值问题（时谐场)的差分计算 966 数值算例 例1矩形金属波导中的截止波长和场分布 > 差分方程组：[K][]=(kh)[可（矩阵特征值问题） [K):系数矩阵；[】：以网格节点上待求场量？，为分量的列向量（特征向量） √ 特征值：(kh)2=(2π时久)，入=2π/k为截止波长 >连续场中的偏微分方程特征值问题→离散系统中的代数矩阵特征值问题 >矩阵特征值问题求解：迭代法、正交相似变换法（借助Matlab提供的特征值求解工具） >一系列特征值和与这些特征值对应的特征向量 特征向量（模式纵向场分量分布）←，特征值（对应模式的截止波长） 横向场与纵向场的关系给出： 模式的色散特性曲线：B2=o2e-k >伪解：（1)数值解误差： fe (2)亥姆霍兹方程未涉及麦克斯韦散度方程（排除：考察场是否满足麦克斯韦散度方程） 7

7 2.3 特征值问题（时谐场）的差分计算  数值算例  例1 矩形金属波导中的截止波长和场分布  差分方程组： （矩阵特征值问题）  [K]：系数矩阵；[]：以网格节点上待求场量 为分量的列向量（特征向量）  特征值： ， 为截止波长  连续场中的偏微分方程特征值问题离散系统中的代数矩阵特征值问题  矩阵特征值问题求解：迭代法、正交相似变换法（借助Matlab提供的特征值求解工具）  一系列特征值和与这些特征值对应的特征向量 特征向量（模式纵向场分量分布） 特征值（对应模式的截止波长） 横向场与纵向场的关系给出； 模式的色散特性曲线：  伪解：（1）数值解误差； （2）亥姆霍兹方程未涉及麦克斯韦散度方程（排除：考察场是否满足麦克斯韦散度方程） i  fc f

2.3特征值问题（时谐场）的差分计算 数值算例 ◆ 例2方同轴线中高次模的截止波长 >主模为TEM模 >高阶模：TE模 H)、TM模(E,) >确定主模单模工作带宽：需知第一个高阶模的截止频率 8

8 2.3 特征值问题（时谐场）的差分计算  数值算例  例2 方同轴线中高次模的截止波长  主模为TEM模  高阶模：TE模（ ）、TM模（ ）  确定主模单模工作带宽：需知第一个高阶模的截止频率 x y b a

课堂研讨-综合设计（1)-（16) 956 综合设计（1)-（4)（课堂研讨） 用有限差分法求下图所示四种传输线主模(TEM模，Ez=0,Hz=0)的特性阻抗Z0、横截面的电磁场分布。 画出横截面的电磁场分布图、Z0随几何参数b的变化曲线，用多项式拟合给出Z0随ab的变化关系，设仍 的取值范围为0.3~0.7。 (1)写出该电磁场边值问题的偏微分方程形式及边界条件： (2)写出由电磁场解求特性阻抗的方法及公式： (3)离散化场域。给出网格划分的详细图示及文字说明（包括节点编号、网格步长等）； (4)给出从偏微分方程边值问题到差分代数方程组的详细推导过程（包括边界条件的引入过程）： (5)给出程序框图；编程计算； (6)研究网格粗细对结果的影响；写出综合设计报告。 (1) (2) (3) (4) 9

9 课堂研讨-综合设计（1）-（16）  综合设计（1）-（4）（课堂研讨） 用有限差分法求下图所示四种传输线主模（TEM模，Ez=0，Hz=0）的特性阻抗Z0、横截面的电磁场分布。 画出横截面的电磁场分布图、Z0随几何参数 a/b 的变化曲线，用多项式拟合给出Z0随 a/b 的变化关系，设 a/b 的取值范围为0.3~0.7。 （1）写出该电磁场边值问题的偏微分方程形式及边界条件; （2）写出由电磁场解求特性阻抗的方法及公式; （3）离散化场域。给出网格划分的详细图示及文字说明（包括节点编号、网格步长等）; （4）给出从偏微分方程边值问题到差分代数方程组的详细推导过程（包括边界条件的引入过程）; （5）给出程序框图；编程计算； （6）研究网格粗细对结果的影响；写出综合设计报告。 (1) (2) (3) (4)

课堂研讨-综合设计（1)-（16) 966 综合设计（5)-（8)（课堂研讨） 用有限差分法求如图所示(1)金属矩形波导、（2)单脊金属加载矩形波导、（3)双脊金属加载矩形波 导1、(4)双脊金属加载矩形波导Ⅱ的基模及第一个高阶模的色散特性曲线。设=10mm,b-5mm,c=1mm, (=1.5mm,D=3mm (1)写出该电磁场边值问题的偏微分方程形试（亥姆霍兹方程）及边界条件： (2)离散化场域。给出网格划分的详细图示及文字说明（包括节点编号、网格步长等）； (3)给出从偏微分方程边值问题到差分代数方程组的详细推导过程（包括边界条件的引入过程）： (4)给出程序框图；编程计算； (5)研究网格粗细对结果的影响；写出综合设计报告。 N dD- (5) (6) (7) (8) 10

10 课堂研讨-综合设计（1）-（16）  综合设计（5）-（8）（课堂研讨） 用有限差分法求如图所示（1）金属矩形波导、（2）单脊金属加载矩形波导、（3）双脊金属加载矩形波 导I、（4）双脊金属加载矩形波导II 的基模及第一个高阶模的色散特性曲线。设a=10mm, b=5mm, c=1mm, d=1.5mm, D=3mm （1）写出该电磁场边值问题的偏微分方程形式（亥姆霍兹方程）及边界条件; （2）离散化场域。给出网格划分的详细图示及文字说明（包括节点编号、网格步长等）; （3）给出从偏微分方程边值问题到差分代数方程组的详细推导过程（包括边界条件的引入过程）; （4）给出程序框图；编程计算； （5）研究网格粗细对结果的影响；写出综合设计报告。 (5) (6) (7) (8)

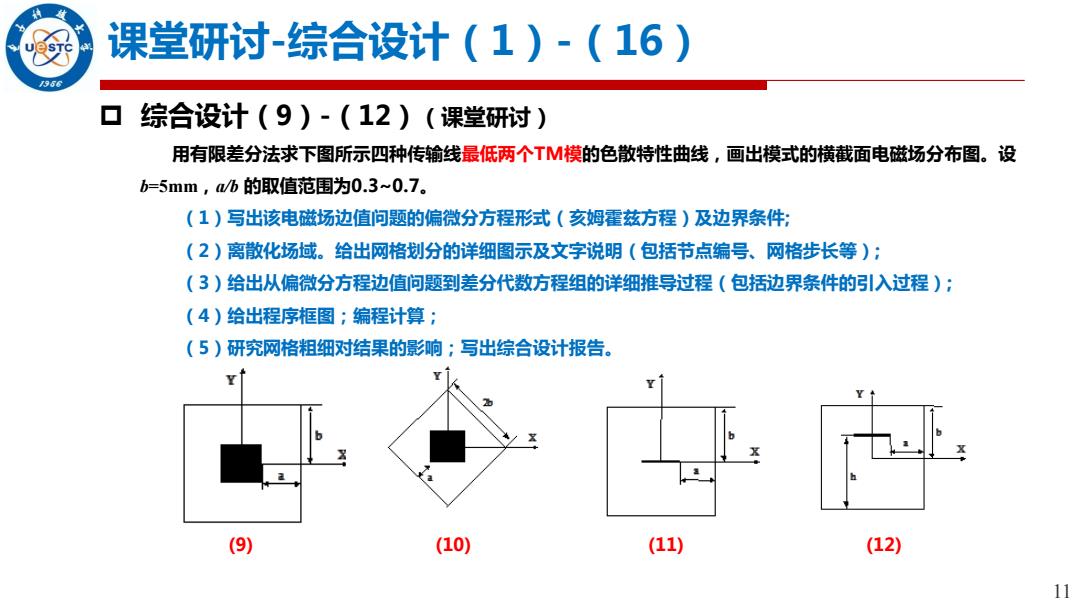
课堂研讨-综合设计（1)-（16) 956 综合设计（9)-（12)（课堂研讨） 用有限差分法求下图所示四种传输线最低两个TM模的色散特性曲线，画出模式的横截面电磁场分布图。设 b=5mm,a/b的取值范围为0.3~0.7。 (1)写出该电磁场边值问题的偏微分方程形式（亥姆霍兹方程）及边界条件： (2)离散化场域。给出网格划分的详细图示及文字说明（包括节点编号、网格步长等）； (3)给出从偏微分方程边值问题到差分代数方程组的详细推导过程（包括边界条件的引入过程）： (4)给出程序框图；编程计算； (5)研究网格粗细对结果的影响；写出综合设计报告。 (9) (10) (11) (12) 11

11 课堂研讨-综合设计（1）-（16）  综合设计（9）-（12）（课堂研讨） 用有限差分法求下图所示四种传输线最低两个TM模的色散特性曲线，画出模式的横截面电磁场分布图。设 b=5mm，a/b 的取值范围为0.3~0.7。 （1）写出该电磁场边值问题的偏微分方程形式（亥姆霍兹方程）及边界条件; （2）离散化场域。给出网格划分的详细图示及文字说明（包括节点编号、网格步长等）; （3）给出从偏微分方程边值问题到差分代数方程组的详细推导过程（包括边界条件的引入过程）; （4）给出程序框图；编程计算； （5）研究网格粗细对结果的影响；写出综合设计报告。 (9) (10) (11) (12)