计算电磁学 (小班研讨课) 966 目录 第十章积分方程 2
2 计算电磁学(小班研讨课) 目 录 第十章 积分方程

10.2磁矢量位和远场近似 10.2.1磁矢量位 >为什么要引入磁矢量位? 观察(8)式: E(r)--jouJG(r.r)J(r)+VV-J(r) dr 已知电流源J,求解电场E,容易 Q:求解困难体现在哪两个方面? 已知电场E,求解电流源J,困难 矩量法 比如,金属散射问题中: ① 已知入射电场E,求解感应电流J,困难 已知感应电流J,求解散射电场E,容易 2 ② 引入磁矢量位有助于简化计算! 金属散射问题
3 10.2 磁矢量位和远场近似 10.2.1 磁矢量位 ➢ 为什么要引入磁矢量位? ( ) ( ) ( ) ( ) 2 1 j , ' ' ' ' ' d ' V G k = − + 观察 E r r r J r J r r (8)式: 已知电流源J,求解电场E,容易 已知电场E,求解电流源J,困难 金属散射问题 比如,金属散射问题中: ① 已知入射电场E0,求解感应电流J,困难 ② 已知感应电流J,求解散射电场E,容易 J J0 E0 ① ② E 矩量法 引入磁矢量位有助于简化计算! Q:求解困难体现在哪两个方面?

10.2磁矢量位和远场近似以 956 在一个媒质为各向同性、无源空间,假设H无散,又H=0,引入磁矢量位A H=LVxA (14) 代入到方程1-1),有 V×E=-joV×A, 矢量的旋度为零,为保守场,等同静电场 Vx(E+j@A)=0 利用矢量恒等式V×(-V)=0,得 电标量位 E=-joA-Vo. (15) 对式(14)两边取旋度,有 矢量恒等式 V×H=V×V×A=V(7·A)-V2A 4
4 10.2 磁矢量位和远场近似 在一个媒质为各向同性、无源空间,假设H无散, = H 0 ,引入磁矢量位A 1 H A = 代入到方程(1-1),有 = − E A j + = (E A j 0 ) 矢量的旋度为零,为保守场,等同静电场 利用矢量恒等式 − = ( e ) 0 ,得 电标量位 e E A = − − j (14) (15) ( ) 2 = = − H A A A 对式(14)两边取旋度,有 矢量恒等式
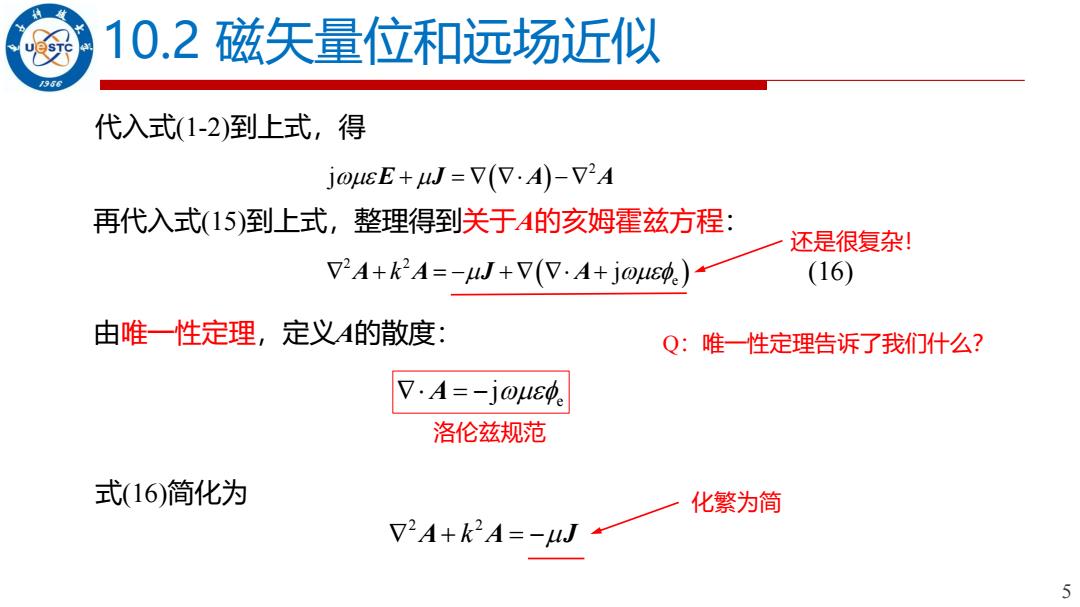
10.2磁矢量位和远场近似 956 代入式1-2)到上式,得 jousE+W=V(7·A-VA 再代入式(15)到上式,整理得到关于A的亥姆霍兹方程: 还是很复杂! V2A+k2A=-WJ+7(7·A+j0u84) (16) 由唯一性定理,定义A的散度: Q:唯一性定理告诉了我们什么? 7·A=-j0ue0 洛伦兹规范 式(16)简化为 化繁为简 V2A+k2A=-uJ 5
5 10.2 磁矢量位和远场近似 代入式(1-2)到上式,得 ( ) 2 j E J A A + = − 再代入式(15)到上式,整理得到关于A的亥姆霍兹方程: ( ) 2 2 e + = − + + A A J A k j 还是很复杂! 由唯一性定理,定义A的散度: Q:唯一性定理告诉了我们什么? e = − A j 洛伦兹规范 式(16)简化为 2 2 + = − A A J k (16) 化繁为简

10.2磁矢量位和远场近似 966 三维情况下,由已知的J和G可以求解A: eik-rj )ufG()( dr (17) (15) E=-j0A---V(V.A) (18) ous 二维情况: A(p)=-j∫J(p)(kp-p >课后阅读 “洛伦兹规范”是哪位学者提出来的?(阅读材料:J.V.Bladel,.“Lorenz or Lorentz?”IEEE Antennas Propag.Magazine,vol.33,pp.69,1991.) 荷兰物理学家H.A.Lorentz 丹麦物理学家L.Lorenz 6
6 10.2 磁矢量位和远场近似 三维情况下,由已知的 J 和 G 可以求解 A: ( ) ( ) ( ) ( ) j ' e , ' ' d ' ' d ' 4 ' k V V G − − = = − r r A r r r J r r J r r r r (15) ( ) j j E A A = − − (17) 二维情况: ( ) ( ) ( ) ( ) 2 0 j ' ' d ' 4 S H k = − − A ρ J ρ ρ ρ ρ ➢ 课后阅读 “洛伦兹规范”是哪位学者提出来的?(阅读材料:J. V. Bladel, “Lorenz or Lorentz?” IEEE Antennas Propag. Magazine, vol. 33, pp. 69, 1991.) 荷兰物理学家 H. A. Lorentz 丹麦物理学家 L. Lorenz ? (18)
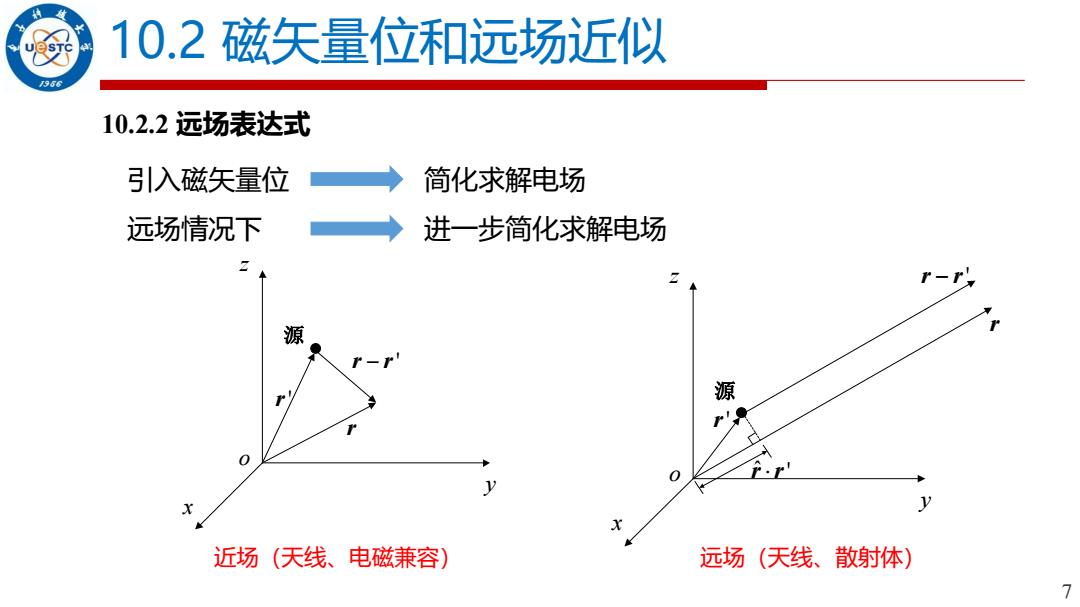
10.2磁矢量位和远场近似 966 10.2.2远场表达式 引入磁矢量位 简化求解电场 远场情况下 进一步简化求解电场 r-r 源 源 0 、之 近场(天线、电磁兼容) 远场(天线、散射体) 7
7 10.2.2 远场表达式 10.2 磁矢量位和远场近似 引入磁矢量位 简化求解电场 远场情况下 进一步简化求解电场 x y z r r ˆ ' r' 源 o r r − ' r x y z r' 源 o r r − ' r 近场(天线、电磁兼容) 远场(天线、散射体)
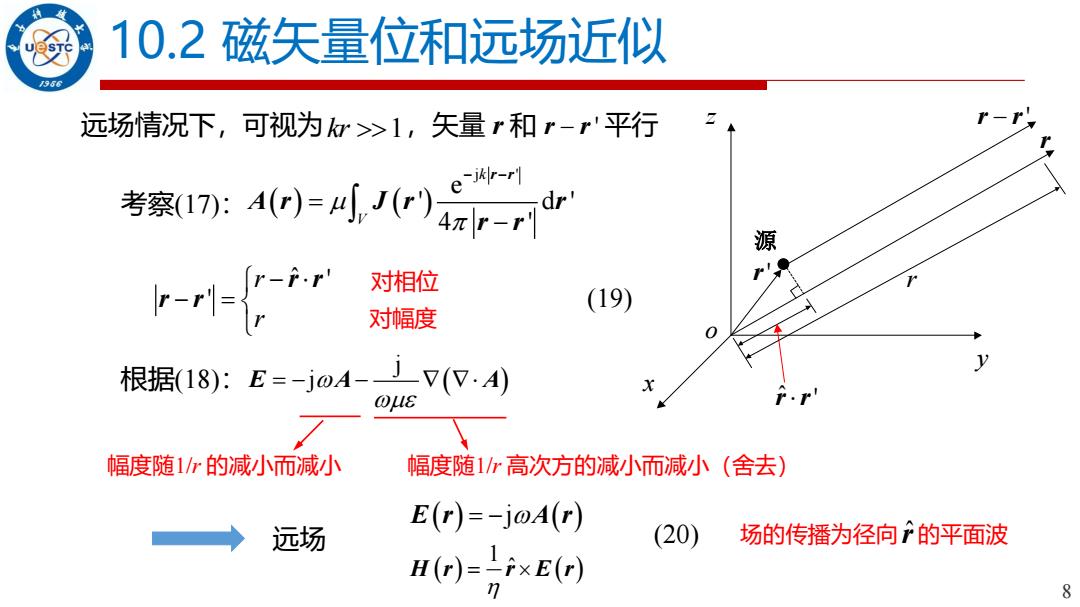
10.2磁矢量位和远场近似 960 远场情况下,可视为>1,矢量r和r-r'平行 r-以 考暴40-小 源 r- r-f.r' 对相位 (19) 对幅度 0 根据(18):E=-joA-」V(V.A) y ous 幅度随1r的减小而减小 幅度随1高次方的减小而减小(舍去) E(r)=-joA(r) 远场 (20) 场的传播为径向P的平面波 H(r)=-ixE(r) 7 P
8 10.2 磁矢量位和远场近似 x y z r r ˆ ' r' 源 o r r − ' r r 远场情况下,可视为 kr 1 ,矢量 r 和 r r − ' 平行 ˆ ' ' r r − − = r r r r 对相位 ( ) ( ) j ' e ' d ' 4 ' k V − − = − r r A r J r r r r 对幅度 考察(17): (19) 根据(18): ( ) j j E A A = − − 幅度随1/r 的减小而减小 幅度随1/r 高次方的减小而减小(舍去) 远场 E r A r ( ) = −j ( ) ( ) ( ) 1 ˆ H r r E r = (20) 场的传播为径向 r ˆ的平面波

10.2磁矢量位和远场近似以 966 > 三维情况,由(19)和(20),得 an-e 和'无关,可置于积分符号外 归一化 雷达散射截面(RCS) 的定义:D=4πr2 4r2E >二维情况,E(p)=-joA(p)=-4J(p)(p-p 利用Hankel函数的大宗量近似(P→oo) 9
9 10.2 磁矢量位和远场近似 ➢ 三维情况,由(19)和(20),得 ( ) ( ) j j ' ˆ j e ' e d ' 4 kr k V r − = − r r E r J r r 和 r ’无关,可置于积分符号外 雷达散射截面(RCS)的定义: 2 s 2 2 2 s 3D 2 i = = 4 4 r r E E E 归一化 ➢ 二维情况, ( ) ( ) ( ) ( ) ( ) 2 0 j = ' ' d ' 4 S H k = − − − E ρ A ρ J ρ ρ ρ ρ 利用Hankel函数的大宗量近似( → ) ( ) ( ) 2 2 j j j en k H k n k −

10.2磁矢量位和远场近似以 966 和-p叶招D 对相位 对幅度 H(k)= 2jepe帅 ( 远场 和p'无关,可置于积分符号外 二维雷达散射截面(RCS)的定义:oD=2πr E a2xrlEri 10
10 10.2 磁矢量位和远场近似 ˆ ' ' − − = ρ ρ 和 ρ ρ 对相位 对幅度 ( ) ( ) 2 j j ' ˆ 0 2 j e e k k H k k − ρ ρ 远场 ( ) ( ) j j ' ˆ j e ' e d ' 8 k k S k − ρ ρ E ρ J ρ ρ 和 ρ ’无关,可置于积分符号外 二维雷达散射截面(RCS)的定义: 2 s 2 s 2D 2 i = = 2 2 r r E E E 归一化
10.3表面积分方程 1966 10.3.1理想导体散射场的等效原理 等效原理的理论基础:惠更斯原理 —一波前的每一点是次级球面波的源 △ 平面波 球面波 惠更斯原理说明波的传播 惠更斯原理说明折射现象 11
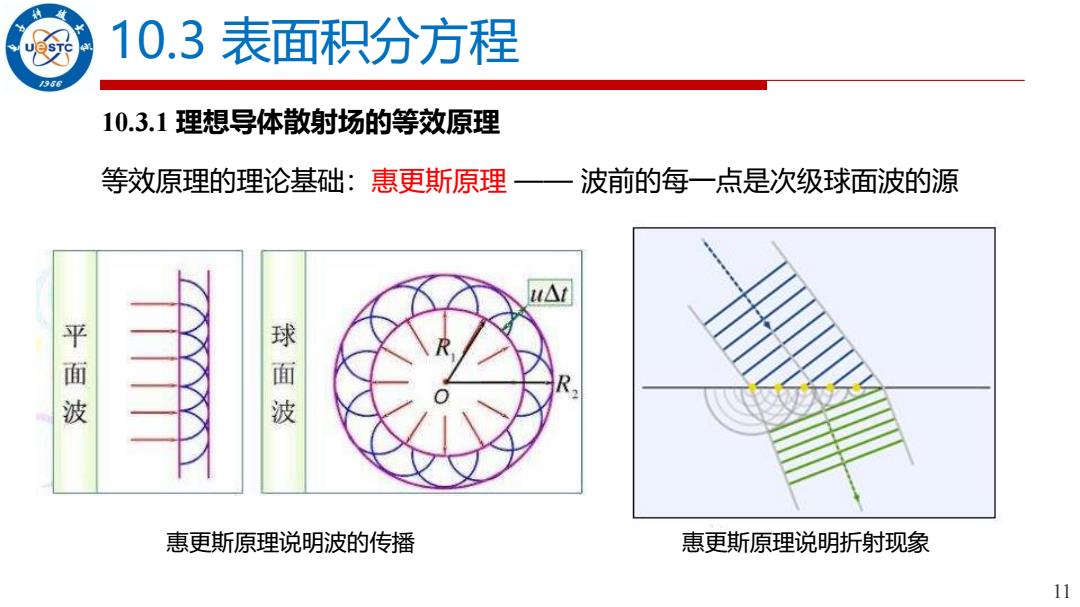
11 10.3.1 理想导体散射场的等效原理 10.3 表面积分方程 等效原理的理论基础:惠更斯原理 —— 波前的每一点是次级球面波的源 惠更斯原理说明波的传播 惠更斯原理说明折射现象