计算电磁学(小班研讨课) 956 第3章频域有限差分法 3.1FDFD基本原理 目 录 3.2吸收边界条件 3.3总场/散射场体系和近远场变换 3.4数值算例(1) 2
2 计算电磁学(小班研讨课) 目 录 第3章 频域有限差分法 3.1 FDFD基本原理 3.2 吸收边界条件 3.3 总场/散射场体系和近远场变换 3.4 数值算例(1)

计算电磁学 第3章频域有限差分法 3
3 第3章 频域有限差分法 计算电磁学

3.1FDFD基本原理 966 频域麦克斯韦方程组的旋度方程 VxE=-jouH-pH VxH=josE+oE >分量式 -jouH,= _{ 2+pH3.3) joE, aA2_, ay (3.6) >2-ja,= aE, E:+pHy Hx (3.4) j0c耳= 0H:-oE, 31) >-jouH,= E,-+p :aw 3.5) josE,= HyOH:-oE: ax ay (3.8) 4
4 3.1 FDFD基本原理 频域麦克斯韦方程组的旋度方程 分量式 (3.3) (3.6) (3.4) (3.7) (3.5) (3.8)
3.1FDFD基本原理 966 Yee的差分网格 (位+1j+1) (+1J+1,+1) 〉离散化场域 网格节点与一组相应的整数标号一一对应 (i,j,k)=(iAx,jAy,kAz) (+1,) 该点的任一函数F(仪,y,z)的值可以表示为 Fi,j,k)=Fi△x,jAy,k△z) FDFD差分格式: Ex (包j+1,+1) >用中心差分将方程中的微分算子→差分形式 郎u四.+-2 +0((Ax 点) 包J+1,) Ox △x ◆ E和H的六个场分量放置方式:每个磁场分量由四个电场分量所环绕 每个电场分量由四个磁场分量所环绕
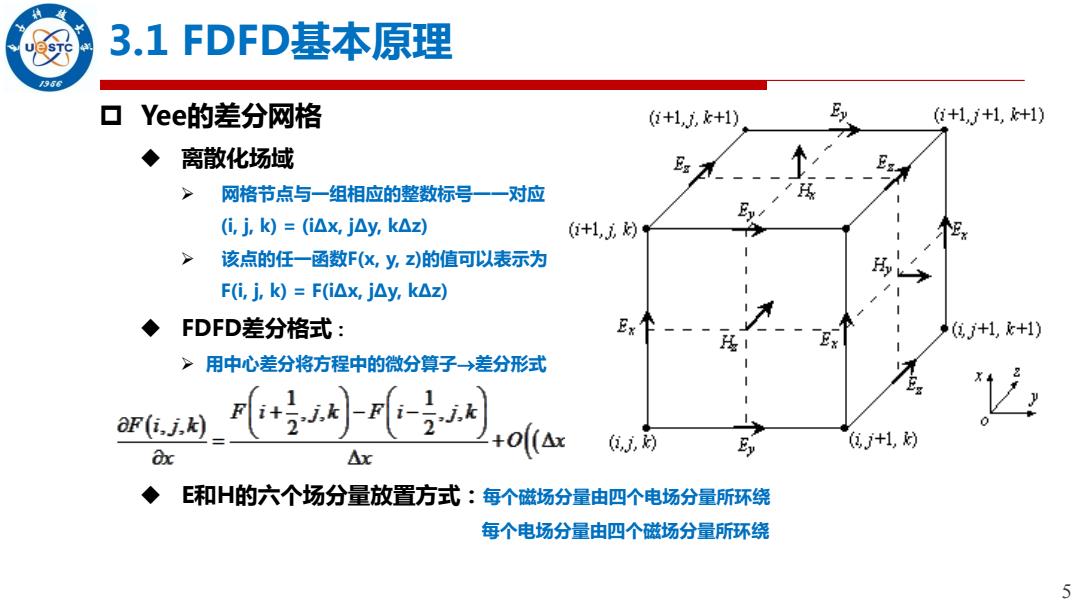
5 3.1 FDFD基本原理 Yee的差分网格 离散化场域 网格节点与一组相应的整数标号一一对应 (i, j, k) = (iΔx, jΔy, kΔz) 该点的任一函数F(x, y, z)的值可以表示为 F(i, j, k) = F(iΔx, jΔy, kΔz) FDFD差分格式: 用中心差分将方程中的微分算子差分形式 E和H的六个场分量放置方式:每个磁场分量由四个电场分量所环绕 每个电场分量由四个磁场分量所环绕

3.1FDFD基本原理 (3.3)式:Hx(i,j+1/2,k+1/2) [-u++)P++(u++ (3.10) E*k+引E+)U++gU+ △y △z ◆(3.4)试:Hy(i+1/2,j,k+1/2) +k+P+ik+,(+k+ +吃k+刊++k+(+ 6
6 3.1 FDFD基本原理 (3.3)式: Hx(i, j+1/2, k+1/2) (3.10) (3.4)式: Hy(i+1/2, j, k+1/2) (3.11)

3.1FDFD基本原理 ◆ (3.5)式:Hz(i+1/2,j+1/2,k) [(+2+(++++刘 (3.12) +w+号U+号++1-+ △C △y ◆(3.6)式:Ex(i+1/2,j,k) i+a+小s+吃内 (3.13) a++-a.+,++g+到 y 7
7 3.1 FDFD基本原理 (3.5)式: Hz(i+1/2, j+1/2, k) ( 3.12 ) (3.6)式: Ex(i+1/2, j, k) (3.13)

3.1FDFD基本原理 (3.7)式:Ey(i,j+1/2,k+1/2) i+号++刘s+ (3.14) ++引++++ △z ◆(3.8)式:Ez(i+1/2,j,k) iuk++ouk+s(u+ (3.15) a+k+引g+时aur时+)u到 △x y (3.10)-(3.15)式:差分方程组;系数矩阵是大型稀疏矩阵 8
8 3.1 FDFD基本原理 (3.7)式: Ey(i, j+1/2, k+1/2) (3.14) (3.8)式: Ez(i+1/2, j, k) (3.15) (3.10)-(3.15)式:差分方程组;系数矩阵是大型稀疏矩阵
3.1FDFD基本原理 966 介质交界面上的差分方程 耳,6+吃k+ >介质无耗,电场分量Ez落在交界面 VxH=josE E.Q.J.k+ HGj5k+) ∫7×H-ds-joeB.ds Ea 应用斯托克斯定理,重。Hl=j询eBdS 用,-+》 面积分 [.-dsw.k+}贤4如+a8k+}y 环职分夷县a以(u-+引++分+日U++A-,-+》A 差分方程 Jo5a5 ))Ax a+号+af-+ 9
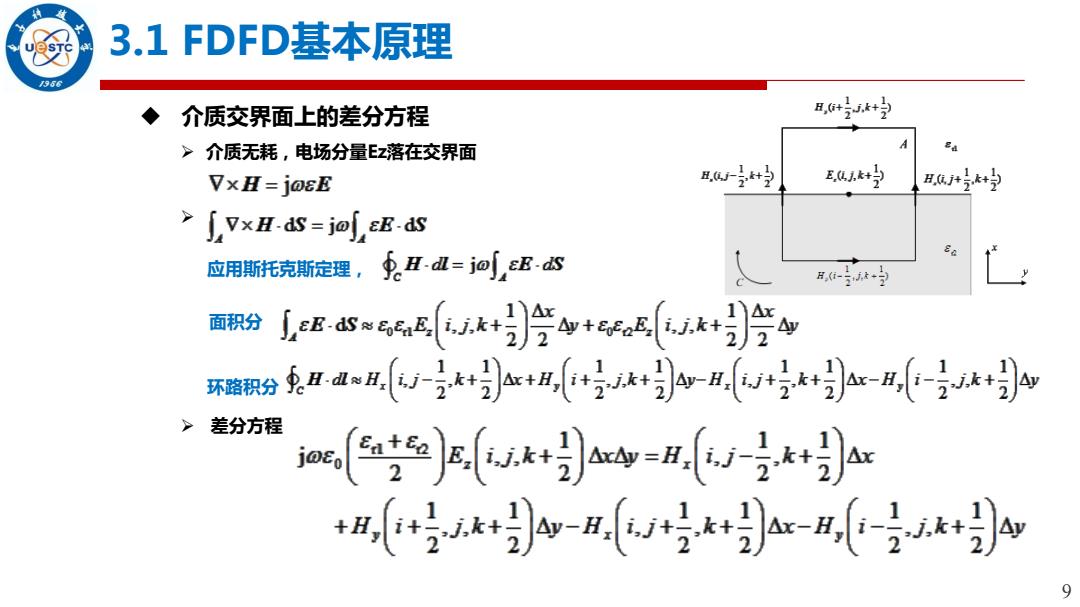
9 3.1 FDFD基本原理 介质交界面上的差分方程 介质无耗,电场分量Ez落在交界面 应用斯托克斯定理, 面积分 环路积分 差分方程

3.1FDFD基本原理 数值色散 >在频域有限差分网格中,数值波模的传播速度将随频率改变,这种改变由非物理因素引起 √人为的各向异性 √数值低通滤波效应 √虚假的折射现象 >数值色散方程(仅考虑无耗、均匀媒质空间) ma(+5四03四ssu* ..共6个FDTD方程 10
10 3.1 FDFD基本原理 数值色散 在频域有限差分网格中,数值波模的传播速度将随频率改变,这种改变由非物理因素引起 人为的各向异性 数值低通滤波效应 虚假的折射现象 数值色散方程(仅考虑无耗、均匀媒质空间) ……共6个FDTD方程
3.1FDFD基本原理 966 数值色散 >单色平面波解: 6j,对=Vep[jk△x+k+kzj] sin k Ax kAy sin OgE,=Hy 2-H; 2 △ 2 2 [B] =0 k△x sin- sin ouH,=E. 2 一E 2 耳 Ay △x 2 2 .…共6个方程 >齐次方程组有非零解的条件 2 dctB(k.k.k.Ax.Ay.Az.0.c.u)= k△x k△y sin k,△z sin sin FDTD的数值色散关系→O孔= 2 2 2 y △z 解析色散关系®'弘=+房+好 2 >△x、△y、△z均趋于零时,数值色散关系→解析色散关系 11
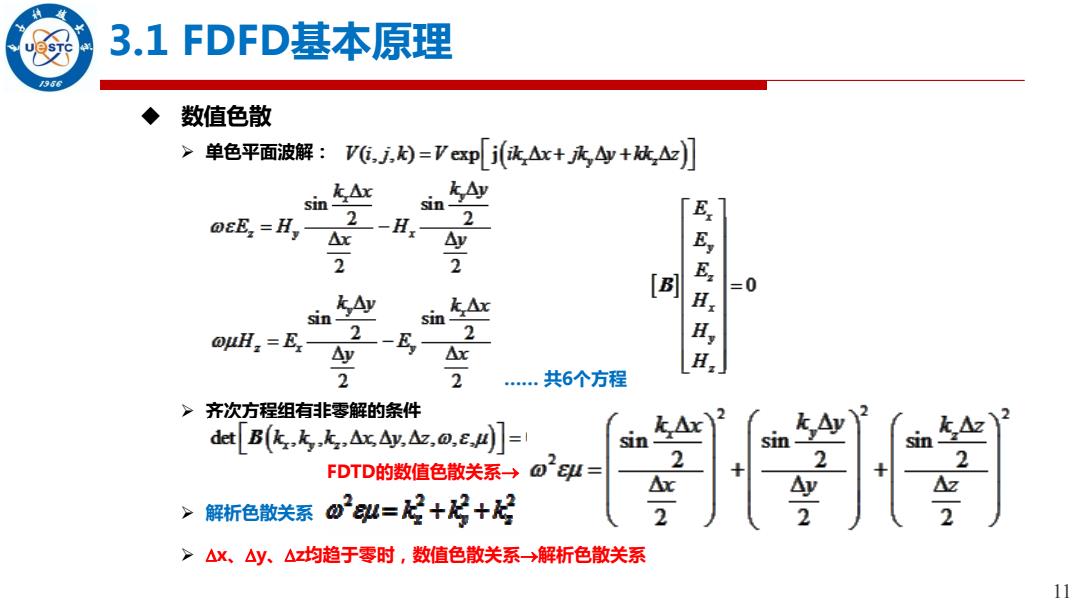
11 3.1 FDFD基本原理 数值色散 单色平面波解: …… 共6个方程 齐次方程组有非零解的条件 FDTD的数值色散关系 解析色散关系 x、y、z均趋于零时,数值色散关系解析色散关系