
第五章: 电磁波的辐射 Electromagnetic Wave Radiation
第五章 电磁波的辐射 Electromagnetic Wave Radiation 1

本章所研究的问题是电磁波的辐射。方 法和稳恒场情况一样,当考虑由电荷、电 流分布激发电磁场的问题时,引入势的概 念来描述电磁场比较方便。 本章首先把势的概念推广到一般变化电 磁场情况,然后通过势来解辐射问题。 2
本章所研究的问题是电磁波的辐射。方 法和稳恒场情况一样,当考虑由电荷、电 流分布激发电磁场的问题时,引入势的概 念来描述电磁场比较方便。 本章首先把势的概念推广到一般变化电 磁场情况,然后通过势来解辐射问题。 2

本章主要闭容 电磁场的矢势和标势 推迟势 电偶极辐射 电磁波的干涉和衍射 电磁场的动量 3
本章主要内容 电磁场的矢势和标势 推迟势 电偶极辐射 电磁波的干涉和衍射 电磁场的动量 3

§5.1电磁场的矢势和标势 Vector and Scalar Potential of Electromagnetic 4
§5. 1 电磁场的矢势和标势 Vector and Scalar Potential of Electromagnetic 4

1、用势A,p描述电磁场 为简单起见,讨论真空中的电磁场: V.D-P VxE=- aB 8t D=6E,B=4,月 V.B=0 V×i=j+ 5
1、用势 描述电磁场 为简单起见,讨论真空中的电磁场: 0 t D H j B t B E D A, , . D 0 E B 0 H 5

针对磁场 V.B=0 引入 B=VxA A的物理意义可由下式看出: fA=j∬B杰 即在任一时刻,矢量A沿任一闭合回路L的线积 分等于该时刻通过以L为边线的曲面S的磁通量。 6
针对磁场 引入 的物理意义可由下式看出: 即在任一时刻,矢量 沿任一闭合回路L的线积 分等于该时刻通过以L为边线的曲面S的磁通量。 B 0 B A L S A dl B ds A A 6

对于电场E不能像静电场那样直接引入电势。由 Faraday电磁感应定律可得: ×E=- ×=-Vx B 4 8t 十 8t E+ A -V→ 是标势不 8t 是静电势 7
对于电场 不能像静电场那样直接引入电势。由 Faraday电磁感应定律可得: E t A A t t B E ( ) 0 t A E t A E 是标势不 是静电势 7
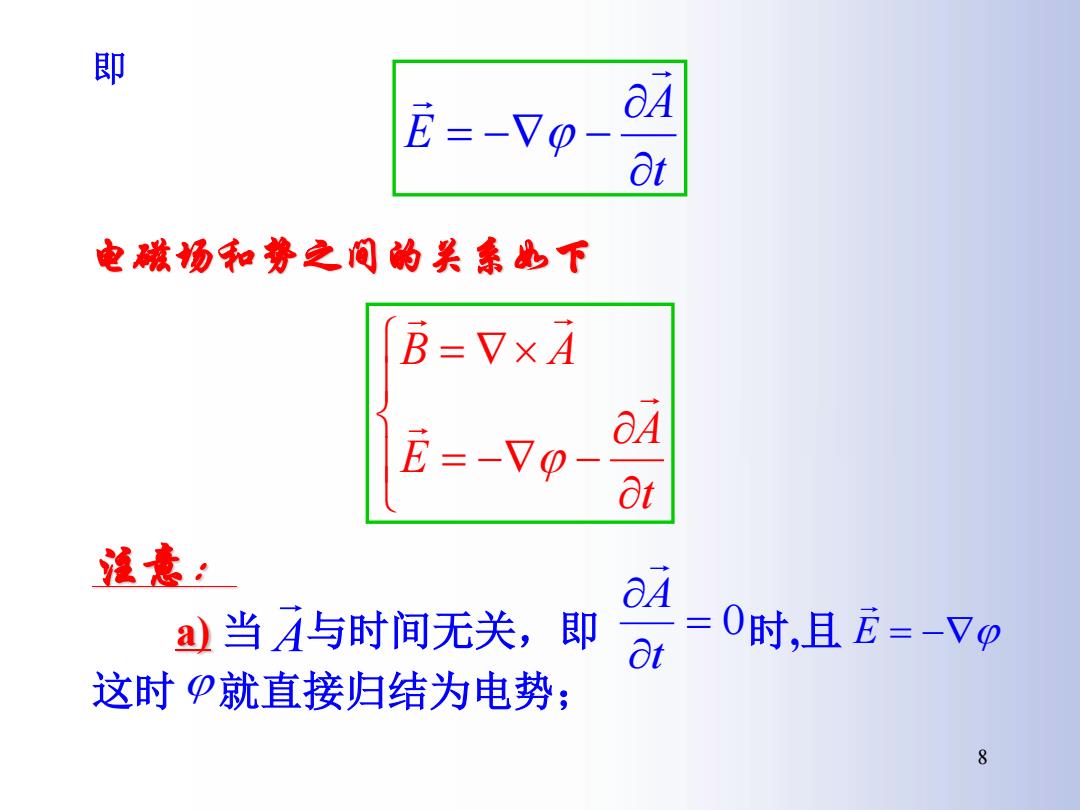
即 6=-Vp- at 电嫩场和势之间的吴素匹下 B=V×A E=-V0- 84 Ot 滋意: 84 a当A与时间无关,即 =0时,且E=-Vp 这时P就直接归结为电势; 8
即 t A E 电磁场和势之间的关系如下 t A E B A 注意: a) 当 与时间无关,即 时,且 这时 就直接归结为电势; A 0 t A E 8

绝对不要把E=-V0 o4 b) 中的标势 8t 与电势o(E=-Vp)混为一谈。因为在非稳恒情 况下,龙不再是保守力场,不存在势能的概念, 这就是说现在的p,在数值上不等于把单位正电 荷从空间一点移到无穷远处电场力所做的功。为 了区别于静电场的电势,把这里的p 称为标势 (Scalar potential)。 c在时变场中,飞 磁场和电场是相互作用着的 整体,必须把矢势A和标势P作为一个整体来描 述电磁场。 9
b) 绝对不要把 中的标势 与电势 混为一谈。因为在非稳恒情 况下, 不再是保守力场,不存在势能的概念, 这就是说现在的 ,在数值上不等于把单位正电 荷从空间一点移到无穷远处电场力所做的功。为 了区别于静电场的电势,把这里的 称为标势 (Scalar potential)。 c) 在时变场中,磁场和电场是相互作用着的 整体,必须把矢势 和标势 作为一个整体来描 述电磁场。 t A E (E ) E A 9

2、规范变换和规范不变性 虽然E和B,以及A和0是描述电磁场的两 种等价的方式,但由于E、B和A、P之间是微分 方程的关系,所以它们之间的关系不是一一对应 的,这是因为矢势A可以加上一个任意标量函数 的梯度,结果不影响B,而这个任意标量函数 的梯度对E要发生影响,但将 E=-V0 8t 中的与此融合也作相应的变换,则仍可使E保 持不变。 10
2、规范变换和规范不变性 虽然 和 ,以及 和 是描述电磁场的两 种等价的方式,但由于 、 和 、 之间是微分 方程的关系,所以它们之间的关系不是一一对应 的,这是因为矢势 可以加上一个任意标量函数 的梯度,结果不影响 ,而这个任意标量函数 的梯度对 要发生影响,但将 中的 与此融合也作相应的变换,则仍可使 保 持不变。 E B A E B A A B E t A E E 10