计算电磁学 (小班研讨课) 966 第8章矩量法基本原理 目录 2
2 计算电磁学(小班研讨课) 目 录 第8章 矩量法基本原理

8.2静电场中的矩量法 8.2.1一维平行板电容器 两板间的电荷密度:p=6(1+4x2) 求解电容器两板间的电位分布。 (1)解析解 解:在区间x∈[0,1]上,电位分布0满足泊松方程 股会+4) 其中,边界条件为0(0)=0(1)=0 可对泊松方程进行两次积分,并代入边界条件,可得 o)-ix-3x-jx 3
3 8.2 静电场中的矩量法 8.2.1 一维平行板电容器 0 1 x ( ) 2 0 两板间的电荷密度: = +1 4x (1)解析解 解:在区间x∈[0, 1]上,电位分布φ 满足泊松方程 ( ) 2 2 2 0 d 1 4 d x x = − = − + 其中,边界条件为φ(0) = φ(1) = 0 可对泊松方程进行两次积分,并代入边界条件,可得 ( ) 5 1 1 2 4 6 2 3 x x x x = − − 求解电容器两板间的电位分布

8.2静电场中的矩量法 956 (2)数值解 (MoM) 在区间x∈[0,1]上,电位分布0满足泊松方程 将用已知的全域基函数展开:p=之,0.=立a,(-x") 代入到泊松方程中,可得 Q1:为什么选择这样的基函数? 立a-r)-0+) Q2:方程是否可解?为什么? = 权函数采用点匹配法,在区间x∈[0,1]上选择N个离散点满足方程,即将该区间等 分为N+1个小区域,匹配点的位置为,xm=m/(N+1),m=1,2,,N,则 -x)=n+x.=n+》 1+4.=1+4 4
4 8.2 静电场中的矩量法 (2)数值解(MoM) 在区间x∈[0, 1]上,电位分布φ 满足泊松方程 将φ用已知的全域基函数展开: ( ) 1 1 1 N N n n n n n n a a x x + = = = = − 代入到泊松方程中,可得 Q1:为什么选择这样的基函数? ( ) ( ) 2 1 2 2 1 d 1 4 d N n n n a x x x x + = − = − + Q2:方程是否可解?为什么? 权函数采用点匹配法,在区间x∈[0, 1]上选择N个离散点满足方程,即将该区间等 分为N+1个小区域,匹配点的位置为, x m N m = + ( 1) ,m = 1, 2, …, N,则 ( ) ( ) ( ) 1 2 1 1 2 d 1 1 d 1 m n n n x x m x x n n x n n x N − + − = − = + = + + 2 2 1 4 1 4 m 1 x x m x = N + = + +

8.2静电场中的矩量法 当W=1时,解得a1=1。代入方程,得 0≈419=x-x2 当N=2时,有 ]. 解得a1=1/18,a2=2/3,代入方程得 *a9+a明- -1-2x 1818 3 22/3 3/4 5/4 当N=3时,有 23 3 42 2 。 解得a1=1/2,a2=0,a3=1/3,则 2 9/227/4a, 13/4 5 1 0≈419+a202+a03=5X1 数值解和解析解一致! 6
5 8.2 静电场中的矩量法 当N = 1时,解得 a1 = 1。代入方程,得 2 1 1 = − a x x 当N = 2时,有 。 1 2 2 2 13 9 2 4 25 9 a a = 解得a1 = 1/18, a2 = 2/3,代入方程得 2 3 1 1 2 2 13 1 2 18 18 3 + = − − a a x x x 1 2 3 2 2 3 3 4 5 4 2 3 3 2 2 9 2 27 4 13 4 a a a = 当N = 3时,有 。解得a1 = 1/2, a2 = 0, a3 = 1/3,则 2 4 1 1 2 2 3 3 5 1 1 6 2 3 + + = − − a a a x x x 数值解和解析解一致!
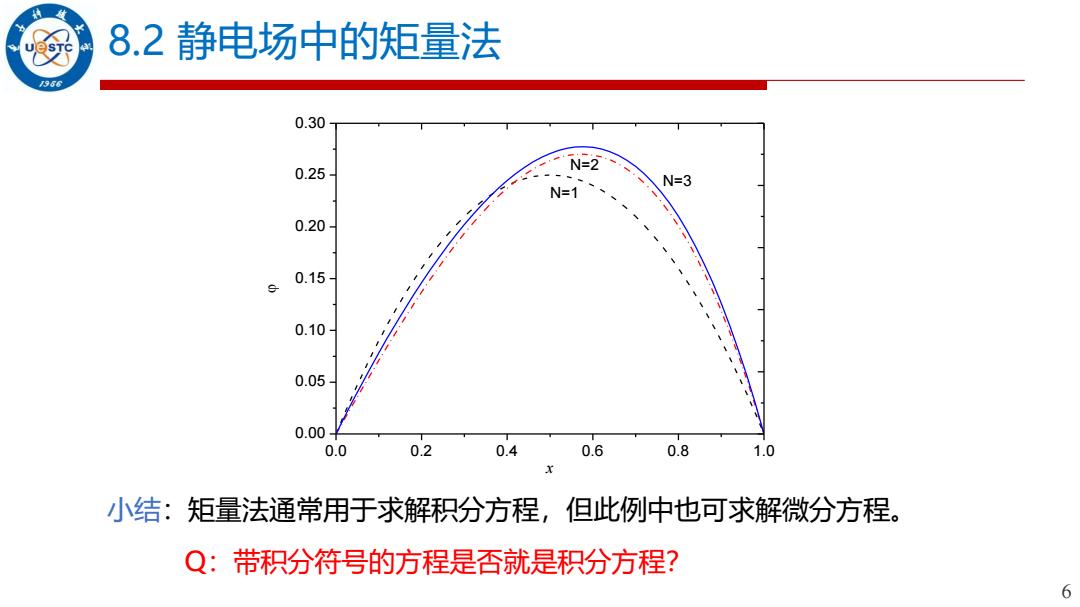
8.2静电场中的矩量法 966 0.30 N=2 0.25 N=3 N=1 0.20 0.15 0.10 0.05 0.00 0.0 0.2 0.4 0.6 0.8 1.0 小结:矩量法通常用于求解积分方程, 但此例中也可求解微分方程。 Q:带积分符号的方程是否就是积分方程? 6
6 8.2 静电场中的矩量法 0.0 0.2 0.4 0.6 0.8 1.0 0.00 0.05 0.10 0.15 0.20 0.25 0.30 N=3 N=2 N=1 x 小结:矩量法通常用于求解积分方程,但此例中也可求解微分方程。 Q:带积分符号的方程是否就是积分方程?

8.2静电场中的矩量法 8.2.2一维带电细导线 2a 当a<L时,求解导线上的电荷密度分布 预备知识:电荷密度g.(r)在r处产生的电位 源点 格林(Green)函数 场点 0-, qe(r')dr G(r,r')= (5) 4πr-r 当已知电位,求解未知的电荷密度,则用数值算法。 解:导线上的电位可用下列一维积分表示 ao-2 (6) 其中,r-r1=Vx-x')2+(y-y)2 Q:为什么一维积分还涉及y? 7
7 8.2 静电场中的矩量法 8.2.2 一维带电细导线 x y 2a L 当a << L时,求解导线上的电荷密度分布 解:导线上的电位可用下列一维积分表示 预备知识:电荷密度qe (r’)在r 处产生的电位 ( ) e ( ) e ' d ' 4 ' V q = − r r r r r 场点 源点 格林(Green)函数 1 ( , ') 4 ' G = − r r r r 当已知电位,求解未知的电荷密度,则用数值算法。 ( ) e ( ) e 0 ' d ' 4 ' L q x x = − r r r (5) (6) ( ) ( ) 2 2 其中,r r − = − + − ' ' ' x x y y Q:为什么一维积分还涉及y?

8.2静电场中的矩量法 96 将导线平均分为W段,每段长△x, Vx-x')2+a2 △x 设每段上的电荷密度q是一个不变量。 XN 将q.(x)用脉冲基函数f,展开 g.(x))=∑af(x) (7) n= 令细导线的电位.()=1V,式(7)代入式(6),并利用脉冲函数定义,得 即:源点和场点都在细线上 字p'= (8) 为避免积分的奇异性,选取源点位于圆柱导体轴线上、」 场点于表面,有 lr-r'=V(x-x)+a 1.物理解释 2.数学解释 8
8 8.2 静电场中的矩量法 x y x 2a 1 x 2 x Nx ( ) 2 2 将导线平均分为 x x a − + ' N段,每段长 , 设每段上的电荷密度qe是一个不变量。 x 将 q x e ( ') 用脉冲基函数 f n展开 e ( ) ( ) 1 ' ' N n n n q x a f x = = (7) 令细导线的电位 e (r) =1V ,式(7)代入式(6),并利用脉冲函数定义,得 ( 1) 1 1 1 d ' 1 4 ' N n x n n x n a x + = = − r r (8) 即:源点和场点都在细线上 为避免积分的奇异性,选取源点位于圆柱导体轴线上、场点于表面,有 ( ) 2 2 r r − = − + ' ' x x a 1.物理解释 2.数学解释

8.2静电场中的矩量法 96 权函数采用点匹配法, 选择N个位于导体表面的独立场点xm,m=1,2,,N, 并位于各分段的中点,可得方程组 dxo-m a NA dx'=4π8 M(x-x)+a -dx'=4π8 (9) Za=b dx'=4π8 其中, 矩阵的元素-心.一+ dx',常向量b的元素bnm=4π6 对称的Toeplitz矩阵,求解参考:G.H.戈卢布《矩阵计算》,科学出版社
9 8.2 静电场中的矩量法 权函数采用点匹配法,选择N个位于导体表面的独立场点xm,m = 1, 2, …, N, 并位于各分段的中点,可得方程组 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 0 1 2 2 2 2 1 1 1 0 1 2 2 2 2 2 2 1 0 1 2 2 2 2 1 1 d ' ... d ' 4 ' ' 1 1 d ' ... d ' 4 ' ' 1 1 d ' ... d ' 4 ' ' x N x N N x x N x N N x x N x N N x N N a x a x x x a x x a a x a x x x a x x a a x a x x x a x x a − − − + + = − + − + + + = − + − + + + = − + − + (9) 其中,矩阵Z的元素 ,常向量b的元素 ( ) ( 1) 2 2 1 d ' ' n x mn n x m z x x x a − = − + 4 m b = Za = b 对称的Toeplitz矩阵,求解参考:G. H. 戈卢布《矩阵计算》,科学出版社
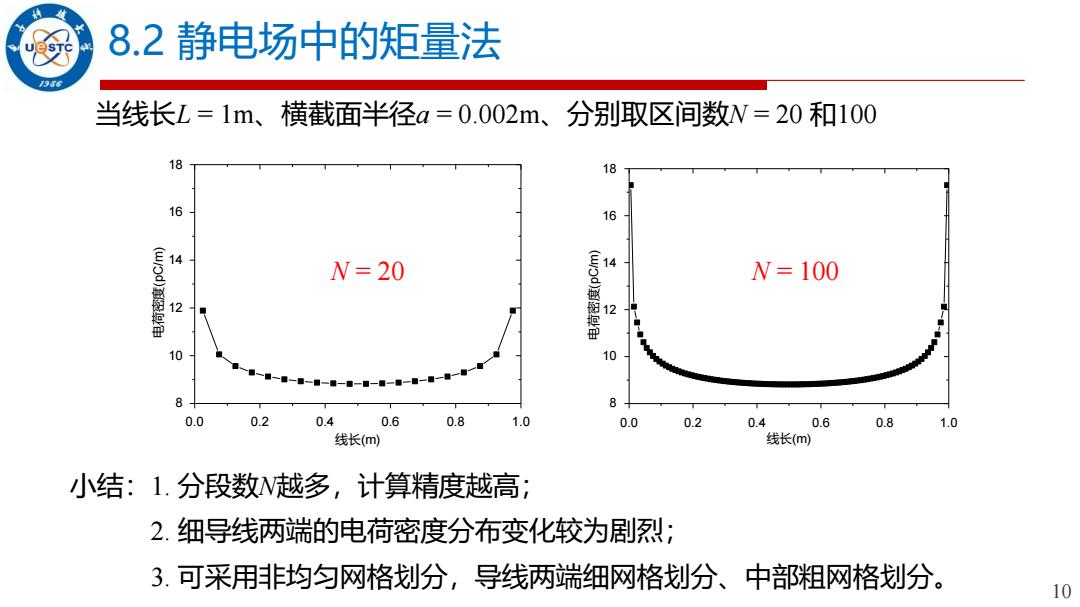
8.2静电场中的矩量法 966 当线长L=1m、横截面半径a=0.002m、 分别取区间数N=20和100 18 18 16 16 4 N=20 14 N=100 12 12 10 10 一■一一 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.40.6 0.8 1.0 线长(m) 线长(m) 小结:1.分段数W越多,计算精度越高; 2.细导线两端的电荷密度分布变化较为剧烈; 3.可采用非均匀网格划分,导线两端细网格划分、中部粗网格划分。 10
10 8.2 静电场中的矩量法 当线长L = 1m、横截面半径a = 0.002m、分别取区间数N = 20 和100 小结:1. 分段数N越多,计算精度越高; 2. 细导线两端的电荷密度分布变化较为剧烈; 3. 可采用非均匀网格划分,导线两端细网格划分、中部粗网格划分。 0.0 0.2 0.4 0.6 0.8 1.0 8 10 12 14 16 18 电荷密度(pC/m) 线长(m) N = 20 0.0 0.2 0.4 0.6 0.8 1.0 8 10 12 14 16 18 电荷密度(pC/m) 线长(m) N = 100
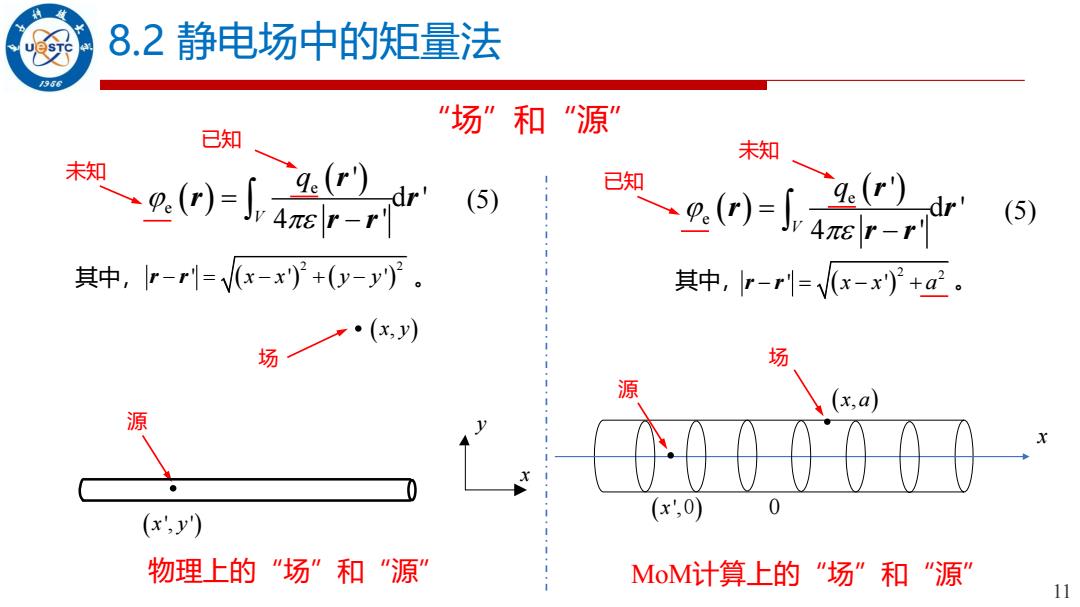
8.2静电场中的矩量法 966 "场”和"源” 已知 未知 未知 (5) 已知 -2 (5) 其中,r-r1=x-x)+y-。 其中,r-r=x-x+a。 ·(x,y) 场 场 源 (xa) 源 (x',y') (x',0) 物理上的"场”和“源' MoM计算上的"场”和"源” 11
11 “场”和“源” 其中, 。 其中, 。 x ( x y ', ') 源 场 MoM计算上的“场”和“源” 源 ( x ',0) 场 0 ( x a, ) 8.2 静电场中的矩量法 ( ) e ( ) e ' d ' 4 ' V q = − r r r r r x y ( ) ( ) 2 2 r r − = − + − ' ' ' x x y y( x y, ) 未知 物理上的“场”和“源” 已知 (5) ( ) 2 2 r r − = − + ' ' x x a ( ) e ( ) e ' d ' 4 ' V q = − r r r r r 已知 未知 (5)