计算电磁学(小班研讨课) 第6章时域有限差分法 6.1激励源技术 目录 6.2集总参数电路元件的模拟 6.3数字信号处理技术 6.4应用举例(0) 2
2 计算电磁学(小班研讨课) 目 录 第6章 时域有限差分法 III 6.1 激励源技术 6.2 集总参数电路元件的模拟 6.3 数字信号处理技术 6.4 应用举例(I)

计算电磁学 966 第6章时域有限差分法川 应用 3
3 第6章 时域有限差分法 III ——应用 计算电磁学

6.1激励源技术 966 强迫激励源 强迫激励源:在FDTD网格中,直接对特定的电磁场分量强行赋予所需的时空变化 >考虑一个一维网格例子,x为传播方向,电场只有Ez分量,点激励源位于x=。△x处 连续正弦波源 E()=Esin(2πfn△t)(在n=0时开通, 位于网格点1、处) 高斯脉冲 ()-e 1=n△1;T=ndecay△ n-n ndecay 有效脉冲宽度:6T(以to为中心) 傅立叶变换: G(f)e-rrr 有效频谱范围: DC-fu:fe=12D;(e4≈8%) 4
4 6.1 激励源技术 强迫激励源 强迫激励源:在FDTD网格中,直接对特定的电磁场分量强行赋予所需的时空变化 考虑一个一维网格例子,x为传播方向,电场只有Ez分量,点激励源位于x= x 处 连续正弦波源 (在n=0时开通,位于网格点 处) 高斯脉冲 有效脉冲宽度:6T(以t0为中心) 傅立叶变换: 有效频谱范围: DC~fmax; fmax=1/(2T) ; ( ) s 0 0 sin 2 n E i E f n t z s i 2 2 0 0 decay decay ; s 0 0 n n t t t n t T n t n n T E i E e E e z 2 2 2 ( ) ~ T f G f e 2 / 4 e 8% s i

6.1激励源技术 强迫激励源 调制高斯脉冲 如果想使直流分量为零,有效频谱中心位于不,可以采用调制高斯脉冲 8(t)→G(f) g(t)cos(2zfu)<>j[G(f+f)+G(f-f)] EW=ee sin[2元f(n-n,)M] 5
5 6.1 激励源技术 强迫激励源 调制高斯脉冲 如果想使直流分量为零,有效频谱中心位于f0,可以采用调制高斯脉冲 g t G f 0 0 0 1 cos 2 2 g t f t G f f G f f 2 0 decay s 0 0 0 sin 2 n n n n E i E e f n n t z

6.1激励源技术 966 强迫激励源 sin(Qt /2) >抽样函数 g(t)= 2t/2 傅里叶变换: cUn-(+--) 2π 在 调制抽样函数 当研究具有一定工作频带的电磁结构(如单模工作波导)时,上述频谱限带信号最合适 刚:工作带宽为是,中心频率为人。,可取E亿,)=E。 sin[2(t-T)/2 cos(2πft) 2π 2(t-T)/2 6
6 6.1 激励源技术 强迫激励源 抽样函数 傅里叶变换: 在 通带内的频谱均匀分布的信号 取主峰前后 2T 范围内的波形,例如,取 考虑到FDTD执行时间从0开始,将时域波形平移T 调制抽样函数 当研究具有一定工作频带的电磁结构(如单模工作波导)时,上述频谱限带信号最合适 例:工作带宽为 ,中心频率为 ,可取 g t t t ( ) sin / / 2 2 G( f ) U f U f 2 4 4 4 4 f 2 40 2 T g t t T t T ( ) sin / / 2 2 2 c f s 0 c sin / 2 cos 2 / 2 n z t T E i E f t t T
6.1激励源技术 966 FDTD时间步进终止条件 >激励源产生数值波→波与被研究结构相互作用(传播与散射) →瞬态过程消失→FDTD时间步进终止 >时间有限脉冲激励(高斯、调制高斯、抽样、调制抽样) 仿真区 瞬态过程消失:波已离开仿真区域→FDTD时间步进终止 >连续正弦波源激励 瞬态过程消失:正弦稳态场已建立→FDTD时间步进终止 >稳态源激励下场达到稳定所需的时间 ■结构的复杂程度及其性质 ■对多数结构,电磁波至少要在其内部传播两个来回 ■对高Q谐振结构,场达到稳定所需的时间则更长 ■表6-1(通过数值实验获得的使场达到稳定所需的时间) 7
7 6.1 激励源技术 FDTD时间步进终止条件 激励源产生数值波波与被研究结构相互作用(传播与散射) 瞬态过程消失FDTD时间步进终止 时间有限脉冲激励(高斯、调制高斯、抽样、调制抽样) 瞬态过程消失:波已离开仿真区域FDTD时间步进终止 连续正弦波源激励 瞬态过程消失:正弦稳态场已建立FDTD时间步进终止 稳态源激励下场达到稳定所需的时间 结构的复杂程度及其性质 对多数结构,电磁波至少要在其内部传播两个来回 对高Q谐振结构,场达到稳定所需的时间则更长 表6-1(通过数值实验获得的使场达到稳定所需的时间)
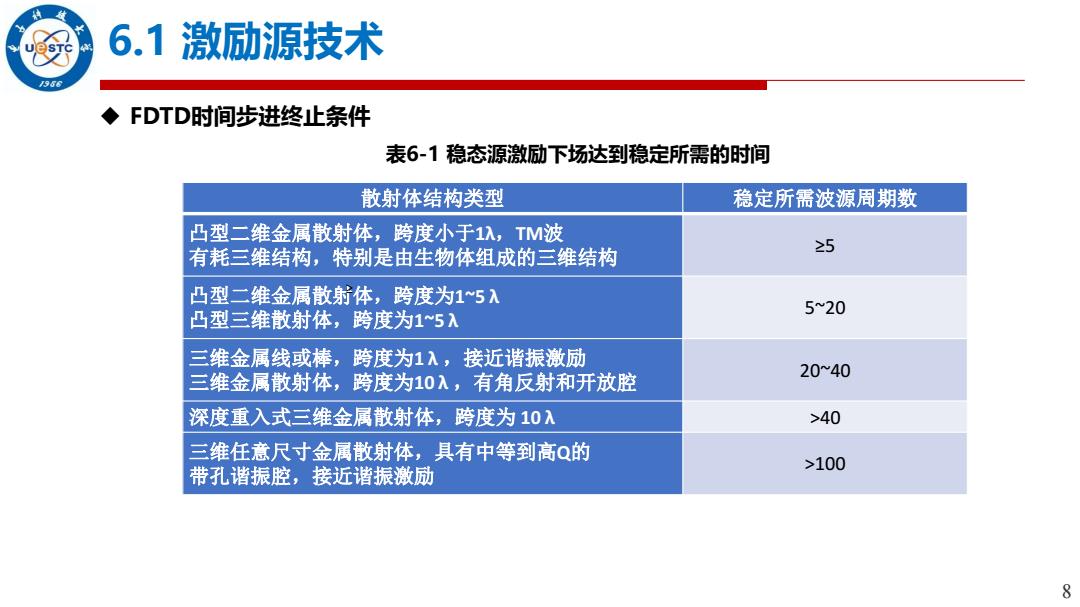
6.1激励源技术 956 FDTD时间步进终止条件 表6-1稳态源激励下场达到稳定所需的时间 散射体结构类型 稳定所需波源周期数 凸型二维金属散射体,跨度小于1入,TM波 有耗三维结构,特别是由生物体组成的三维结构 25 凸型二维金属散射体,跨度为15入 5~20 凸型三维散射体,跨度为15入 三维金属线或棒,跨度为1入, 接近谐振激励 三维金属散射体,跨度为10入,有角反射和开放腔 20~40 深度重入式三维金属散射体,跨度为10入 >40 三维任意尺寸金属散射体,具有中等到高Q的 带孔谐振腔,接近谐振激励 >100 8
8 6.1 激励源技术 FDTD时间步进终止条件 表6-1 稳态源激励下场达到稳定所需的时间 散射体结构类型 稳定所需波源周期数 凸型二维金属散射体,跨度小于1λ,TM波 有耗三维结构,特别是由生物体组成的三维结构 ≥5 凸型二维金属散射体,跨度为1~5 λ 凸型三维散射体,跨度为1~5 λ 5~20 三维金属线或棒,跨度为1 λ ,接近谐振激励 三维金属散射体,跨度为10 λ ,有角反射和开放腔 20~40 深度重入式三维金属散射体,跨度为 10 λ >40 三维任意尺寸金属散射体,具有中等到高Q的 带孔谐振腔,接近谐振激励 >100

6.1激励源技术 虚假反射 >当E”(亿,)≈0时,相当于在网格点。加了一个理想导电反射屏,造成虚假反射 M >简单办法:在激励脉冲几乎衰减为零、来自结构的反射波到达网格点1。之前,将激励源去掉, 网格点1、场值的刷新换用标准FDTD公式 ■不适合式连续正弦波激励源 ·对于宽脉冲激励源,为了使来自结构的反射波到达网格点1。之前激励脉冲几乎衰减为零,网格点。 到结构的距离(隔离段)必需充分大,这将增加计算机内存占用和计算时间 >办法:将激励源看作有源麦克斯韦方程中的一项J, 正-lvxH-1J题,引入FDTD公试 at 8 ■Ez分量的FDTD差分格式 E")=)+×- n+1/2 () 记等效电场激励源为 E)-0),E)=E)+名(x川.+E) 9
9 6.1 激励源技术 虚假反射 当 时,相当于在网格点 加了一个理想导电反射屏,造成虚假反射 简单办法:在激励脉冲几乎衰减为零、来自结构的反射波到达网格点 之前,将激励源去掉, 网格点 场值的刷新换用标准FDTD公式 不适合式连续正弦波激励源 对于宽脉冲激励源,为了使来自结构的反射波到达网格点 之前激励脉冲几乎衰减为零, 网格点 到结构的距离(隔离段)必需充分大,这将增加计算机内存占用和计算时间 办法II:将激励源看作有源麦克斯韦方程中的一项J, , 引入FDTD公式 Ez分量的FDTD差分格式 记等效电场激励源为 , s ( ) 0 n E i z s i s i s i s i s i 1 1 t E H J源 s 1/2 1 1 2 s s , s n n n n z z z z i t t E i E i J i H 源 1 1 2 , s , s n n z z t E i J i 源 源 s 1/2 1 1 s s , s n n n n z z z z i t E i E i E i H 源

6.1激励源技术 966 >办法:将激励源看作有源麦克斯韦方程中的一项J,引入FDTD公式 ■特性 √不会产生虚假反射。E源()=0时,总场E(,)自动退化为标准无源FDTD公式, 不会引入理想导电反射屏 √按总场公式进行,源只是其中单独的一项,当反射波到达时,源是否已消失,不会影响 总场E(,)的正常数值仿真,无需设置隔离段 √等效激励源E()并不等于x=i,△x处的电场值E((,)它只是激励起E(,)的源 √由于这种激励以FDTD公式为载体,它不能放置在仿真区的边界,在那里FDTD公式所 需的域外信息无法得到 ■氵 激励源:电压激励源→电场公式;电流环激励源→磁场公式 10
10 6.1 激励源技术 办法II:将激励源看作有源麦克斯韦方程中的一项J, 引入FDTD公式 特性 不会产生虚假反射。 时,总场 自动退化为标准无源FDTD公式, 不会引入理想导电反射屏 按总场公式进行,源只是其中单独的一项,当反射波到达时,源是否已消失,不会影响 总场 的正常数值仿真,无需设置隔离段 等效激励源 并不等于 处的电场值 ,它只是激励起 的源 由于这种激励以FDTD公式为载体,它不能放置在仿真区的边界,在那里FDTD公式所 需的域外信息无法得到 激励源:电压激励源电场公式 ; 电流环激励源磁场公式 1 , s 0 n E i z 源 1 s n E i z 1 s n E i z 1 , s n E i z 源 s x i x 1 s n E i z 1 s n E i z

6.1激励源技术 时空完整表述的激励源 >源的时间变化(上述例子) >源的空间分布 ■ 波导问题:根据所需模拟的传播模式的时空分布,取某一波导横截面为激励源平面,对位于 该面上的电场切向分量赋予相应的时空变化 ■E0换成相应模式的横截面场分布函数 ■高斯脉冲激励;导波系统的传输方向沿z轴: 模式的横截面场分布为Eo.am(x,) Ejk)-E,Ge=EnL { 强迫激励源加在z=k△二处: ■E。.(化,y)解析已知:数值取样模拟出所需入射波,不会激发起不希望存在的模式 ■E。m(x,y)未知? 11
11 6.1 激励源技术 时空完整表述的激励源 源的时间变化(上述例子) 源的空间分布 波导问题:根据所需模拟的传播模式的时空分布,取某一波导横截面为激励源平面,对位于 该面上的电场切向分量赋予相应的时空变化 E0换成相应模式的横截面场分布函数 高斯脉冲激励;导波系统的传输方向沿 z 轴; 模式的横截面场分布为 ; 强迫激励源加在 处; 解析已知:数值取样模拟出所需入射波,不会激发起不希望存在的模式 未知 ? 0, tan E ( , ) x y s z k z 2 2 0 0 tan s 0, tan 0, tan E E E , , ( , ) ( , ) decay n n t t n n T i j k i j e i j e 0, tan E ( , ) x y 0, tan E ( , ) x y