例 95 目录 第十四章人工神经网络模型 2
2 目 录 第十四章 人工神经网络模型

966 人类的经验: apri A盖系aR B:banao C:banana apricot 微风、晚霞、星星→明天是好天气 apple banana 课堂学习、课后作业、考前复习 →考试取得好成绩 色泽青绿、根蒂蜷缩、敲声浊响 一→正熟的好瓜 3
3 人类的经验: 微风、晚霞、星星 → 明天是好天气 课堂学习、课后作业、考前复习 → 考试取得好成绩 色泽青绿、根蒂蜷缩、敲声浊响 → 正熟的好瓜
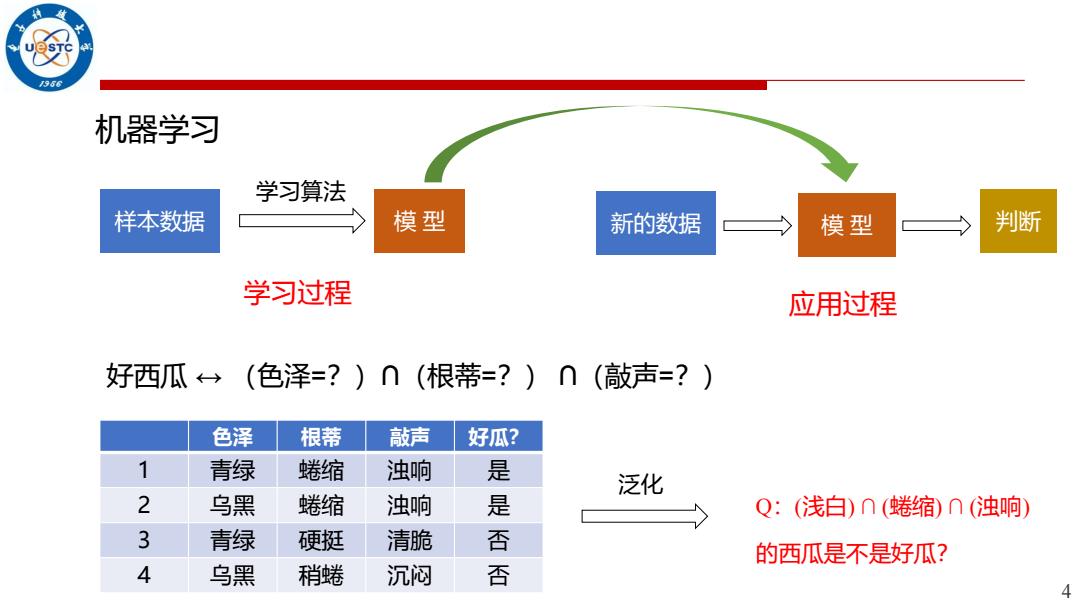
机器学习 学习算法 样本数据 模型 新的数据 模型 判断 学习过程 应用过程 好西瓜←(色泽=?)∩(根蒂=?)∩(敲声=?) 色泽 根蒂 敲声 好瓜? 1 青绿 蜷缩 浊响 是 泛化 2 乌黑 蜷缩 浊响 是 Q:(浅白)∩(蜷缩)∩(浊响) 3 青绿 硬挺 清脆 否 的西瓜是不是好瓜? 4 乌黑 稍蜷 沉闷 否 4
4 机器学习 学习过程 应用过程 样本数据 模 型 学习算法 新的数据 模 型 判断 色泽 根蒂 敲声 好瓜? 1 青绿 蜷缩 浊响 是 2 乌黑 蜷缩 浊响 是 3 青绿 硬挺 清脆 否 4 乌黑 稍蜷 沉闷 否 好西瓜 ↔ (色泽=?)∩(根蒂=?) ∩(敲声=?) 泛化 Q:(浅白) ∩ (蜷缩) ∩ (浊响) 的西瓜是不是好瓜?

斑 966 nature 深度学习 神经网络 机器学习 人工智能 At last-a computer program that can beat a champion Go player ALL SYSTEMS GO WHEN GENI 2016年1月 《Nature)》 2016年3月,Google公司的AlphaG0 以4:1击败围棋世界冠军李世石 5
5 尺度问题 人工智能 机器学习 神经网络 深度学习 2016年1月 《Nature》 2016年3月, Google公司的AlphaGo 以4:1击败围棋世界冠军李世石
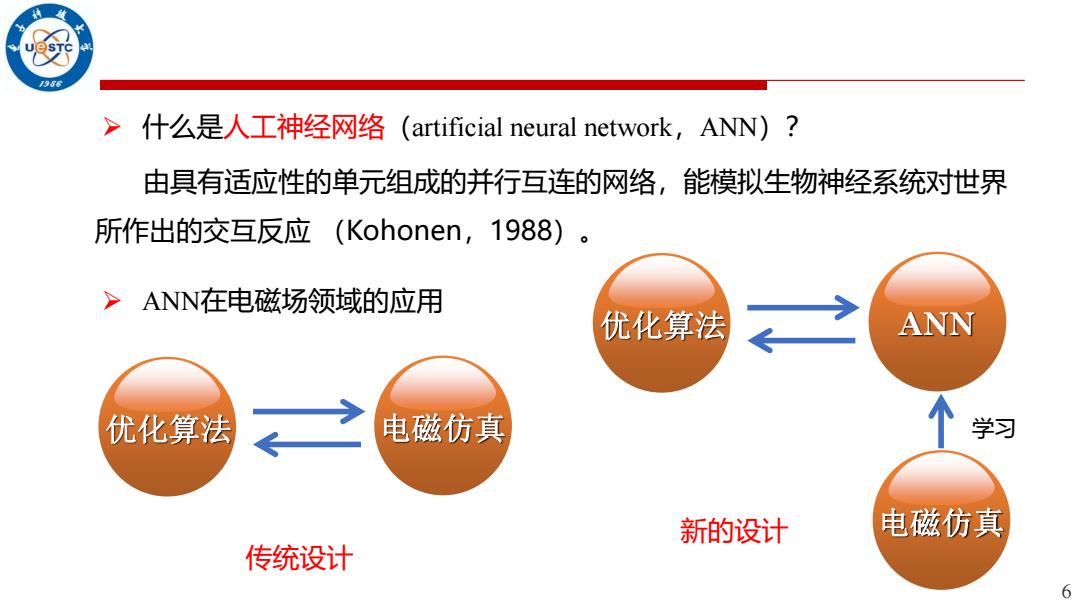
966 >什么是人工神经网络(artificial neural network,ANN)? 由具有适应性的单元组成的并行互连的网络,能模拟生物神经系统对世界 所作出的交互反应(Kohonen,1988) >ANN在电磁场领域的应用 优化算法 ANN 优化算法 电磁仿真 个 学习 新的设计 电磁仿真 传统设计 6
6 ➢ 什么是人工神经网络(artificial neural network,ANN)? 由具有适应性的单元组成的并行互连的网络,能模拟生物神经系统对世界 所作出的交互反应 (Kohonen,1988)。 优化算法 电磁仿真 传统设计 优化算法 ANN 新的设计 电磁仿真 学习 ➢ ANN在电磁场领域的应用
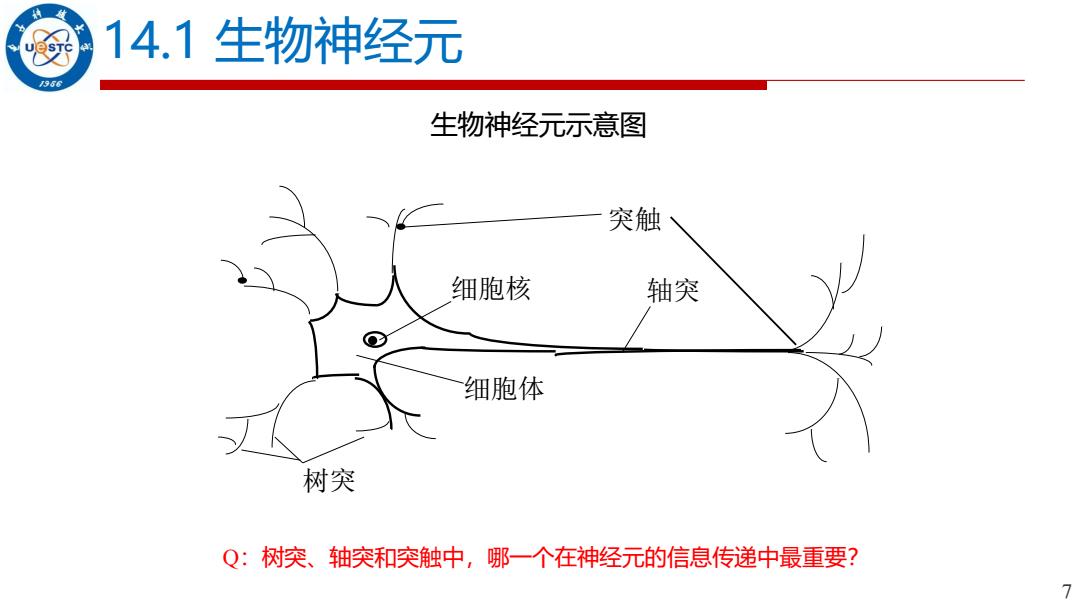
14.1生物神经元 966 生物神经元示意图 突触 细胞核 轴突 细胞体 树突 Q:树突、轴突和突触中,哪一个在神经元的信息传递中最重要? 7
7 14.1 生物神经元 细胞核 细胞体 树突 突触 轴突 生物神经元示意图 Q:树突、轴突和突触中,哪一个在神经元的信息传递中最重要?
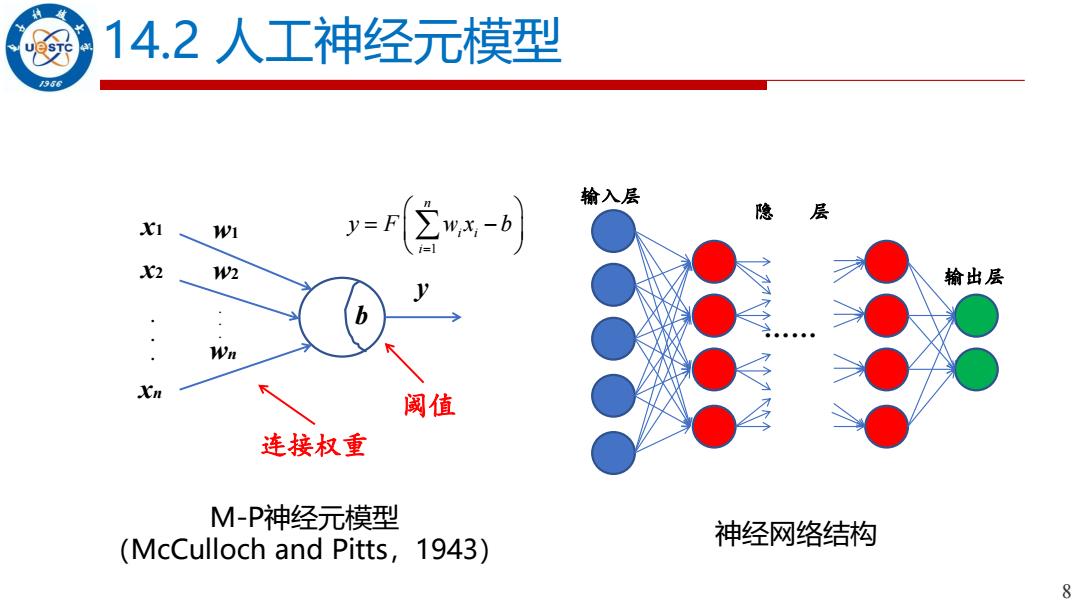
14.2人工神经元模型 1966 输入层 y-Fb 隐 层 W1 X2 W2 输出层 Wn Xn 阈值 连接权重 M-P神经元模型 (McCulloch and Pitts,1943) 神经网络结构 8
8 14.2 人工神经元模型 …… 输出层 隐 层 输入层 x1 x2 xn . . . . . . w1 w2 wn y b 连接权重 阈值 M-P神经元模型 (McCulloch and Pitts,1943) 神经网络结构 1 n i i i y F w x b = = −
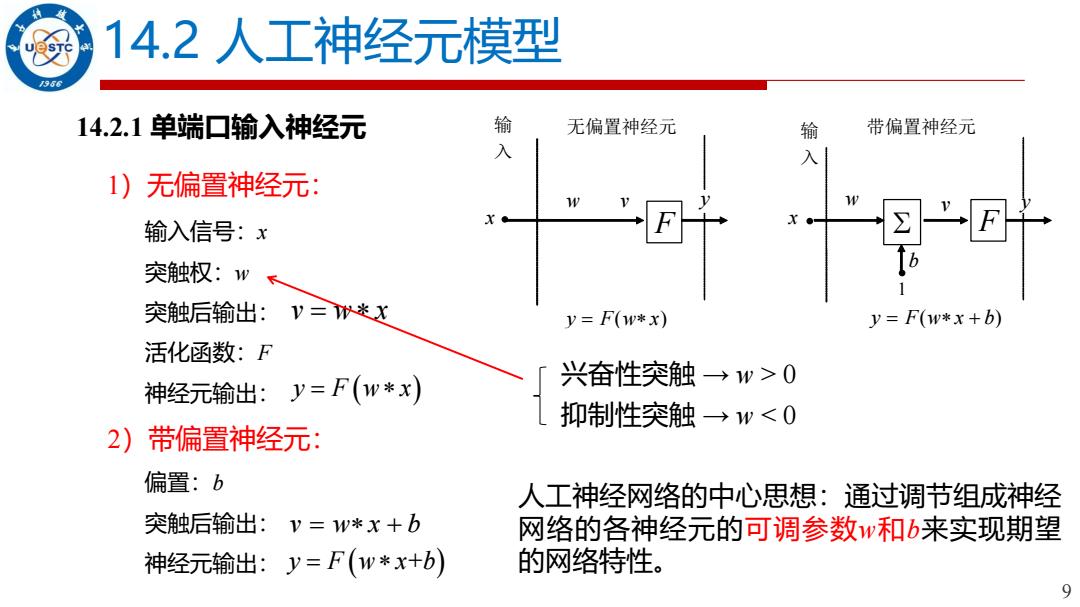
14.2人工神经元模型 14.2.1单端口输入神经元 输 无偏置神经元 输 带偏置神经元 入 1)无偏置神经元: 输入信号:x 突触权:w← w 突触后输出:v三迷x v=F(w*x) =F(1w*x+b) 活化函数:F 神经元输出:y=F(w*x) 兴奋性突触→w>0 抑制性突触 →w<0 2)带偏置神经元: 偏置:b 人工神经网络的中心思想:通过调节组成神经 突触后输出:v=1w*x+b 网络的各神经元的可调参数w和b来实现期望 神经元输出:y=F(w*x+b) 的网络特性。 9
9 14.2 人工神经元模型 14.2.1 单端口输入神经元 F w v 输 入 无偏置神经元 y y = F(w x) F w v 输 入 带偏置神经元 y y = F(w x + b) b x x (a) (b) 1 输入信号:x 突触权:w 突触后输出: 活化函数:F 神经元输出: v w x = 1)无偏置神经元: y F w x = ( ) 2)带偏置神经元: 偏置:b 突触后输出: 神经元输出: v = w x + b y F w x b = ( + ) 兴奋性突触 → w > 0 抑制性突触 → w < 0 人工神经网络的中心思想:通过调节组成神经 网络的各神经元的可调参数w和b来实现期望 的网络特性

14.2人工神经元模型 966 14.2.2活化函数(激活函数,activation function) 活化函数F(v)定义了神经元的输出,它是神经元内部活化位的函数。 1)门限活化函数 1 如果v≥0 如果v<0 0 -b/w 0 Matlab中,门限活化函数名为hardlim y=hardlim(v) y=hardlim(wx+b) 10
10 14.2 人工神经元模型 14.2.2 活化函数(激活函数,activation function) 活化函数F(v)定义了神经元的输出,它是神经元内部活化位v的函数。 1)门限活化函数 F v v v ( ) = 1 0 0 0 如果 如果 y v + 1 − 1 0 + 1 − 1 0 y x − b / w Matlab中,门限活化函数名为 y = hardlim(v) y = hardlim(w* x+b) hardlim
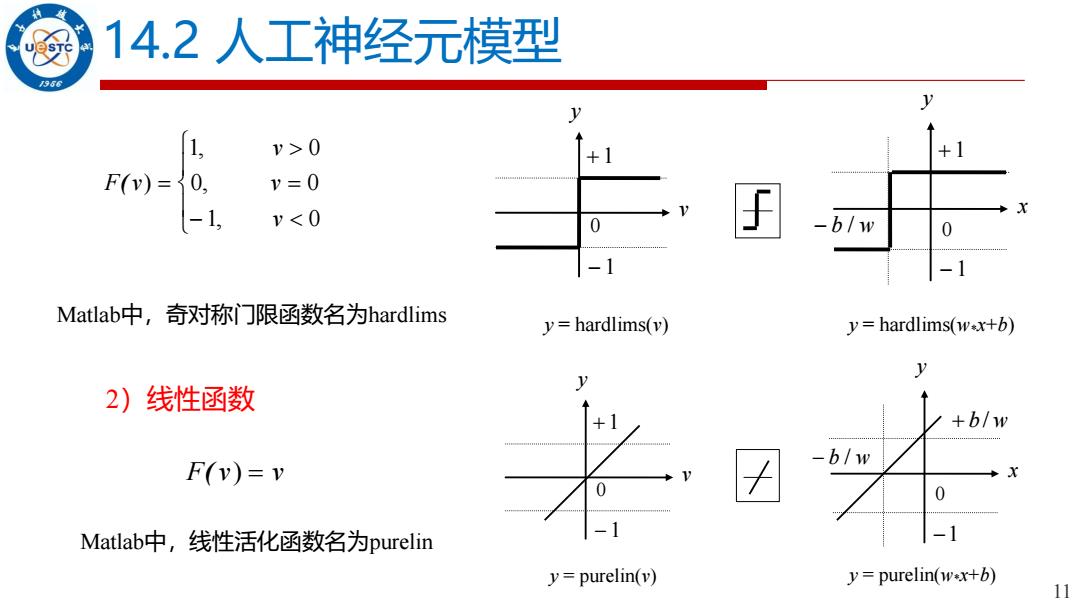
14.2人工神经元模型 966 y 1, v>0 +1 F(v)= v=0 -1 v<0 /w Matlab中,奇对称门限函数名为hardlims y=hardlims(v) y=hardlims(w*x+b) y 2)线性函数 +b/w -b/w F(v)=v Matlab中,线性活化函数名为purelin -1 y=purelin(v) y=purelin(wx+b) 11
11 14.2 人工神经元模型 y v + 1 − 1 0 + 1 − 1 0 y x − b / w y = hardlims(v) y = hardlims(w* x+b) F v v v v ( ) , , , = = − 1 0 0 0 1 0 Matlab中,奇对称门限函数名为hardlims 2)线性函数 F( v) = v Matlab中,线性活化函数名为purelin − b / w y v + 1 − 1 0 + b / w −1 0 y x y = purelin(v) y = purelin(w* x+b)