计算电磁学(小班研讨课) 966 第4章时域有限差分法I 4.1FDTD基本原理 4.2解的稳定性条件 目录 4.3非均匀网格 4.4共形网格 4.5半解析数值模型 4.6良导体中的差分格式 2
2 计算电磁学(小班研讨课) 目 录 第4章 时域有限差分法 I 4.1 FDTD基本原理 4.2 解的稳定性条件 4.3 非均匀网格 4.4 共形网格 4.5 半解析数值模型 4.6 良导体中的差分格式

计算电磁学 966 第4章时域有限差分法I 差分格式及解的稳定性 3
3 第4章 时域有限差分法 I ——差分格式及解的稳定性 计算电磁学
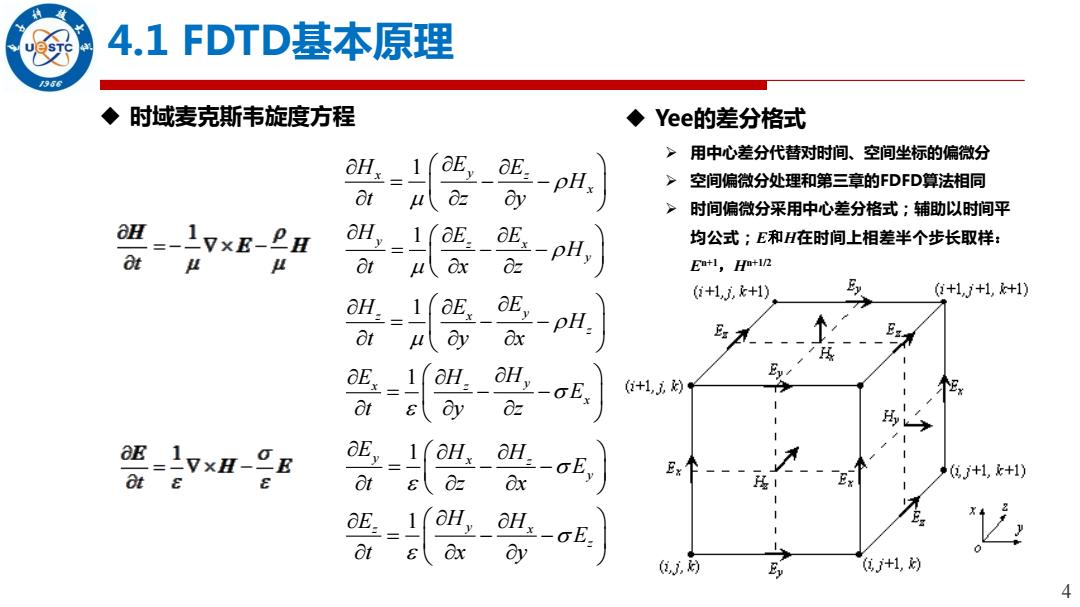
4.1FDTD基本原理 956 ◆时域麦克斯韦旋度方程 ◆Yee的差分格式 OH,1(E, > 用中心差分代替对时间、空间坐标的偏微分 OE. 空间偏微分处理和第三章的FDFD算法相同 8t uz 8y -pH: 时间偏微分采用中心差分格式;辅助以时间平 =-1vxB-PH OH,1(E. aE, 均公式:E和H在时间上相差半个步长取样: 4 u at u Ox 8z -pHy En+l,Ha+in2 (+1,,k+1) E (+1j+1,+1) OH.1(E, E, 8t u by Ox -pH. E:7 盟 H _-oE: +1,) ot dy 02 E,1(OH.OH. Ex Ot s Oz Ox g+1,k+1) Ot Ox 0H.-cE. Cy (,) +1, 4
4 4.1 FDTD基本原理 时域麦克斯韦旋度方程 z 1 x y z H E E H t y x x 1 y z x H E E H t z y y 1 z x y H E E H t x z x 1 z y x E H H E t y z y 1 x z y E H H E t z x z 1 y x z E H H E t x y Yee的差分格式 用中心差分代替对时间、空间坐标的偏微分 空间偏微分处理和第三章的FDFD算法相同 时间偏微分采用中心差分格式;辅助以时间平 均公式;E和H在时间上相差半个步长取样: En+1,Hn+1/2

4.1FDTD基本原理 ◆Yee的差分格式 >Hx展开点(n△t,ix,G+1/2)△y.(k+1/2)△z)→(4.10) ++-c4++rc △ >Hy展开点(nAt,(i+1/2)△x,jy,(k+1/2)△z)→(4.11) …且外 △x >Hz展开点(nAt,(i+1/2)△x,0+1/2)Ay,k△z)→(4.12) cfc5o-eu 5
5 4.1 FDTD基本原理 Yee的差分格式 Hx展开点(nt, ix, (j+1/2)y, (k+1/2)z)(4.10) Hy展开点(nt, (i+1/2)x, jy, (k+1/2)z)(4.11) Hz展开点(nt, (i+1/2)x, (j+1/2)y,kz)(4.12) 1 1 2 2 ,1 ,2 1 1 1 1 , , 1 , , , , , 1, 1 1 1 1 2 2 2 2 , , , , +C 2 2 2 2 n n n n y y z z n n x Hx x Hx E i j k E i j k E i j k E i j k H i j k C H i j k z y 1 1 2 2 ,1 ,2 1 1 1 1 1, , , , , , , , 1 1 1 1 1 2 2 2 2 , , , , 2 2 2 2 n n n n z z x x n n y Hy y Hy E i j k E i j k E i j k E i j k H i j k C H i j k C x z 1 1 2 2 ,1 ,2 1 1 1 1 , 1, , , , , 1, , 1 1 1 1 2 2 2 2 , , , , 2 2 2 2 n n n n x x y y n n z Hz z Hz E i j k E i j k E i j k E i j k H i j k C H i j k C y x

4.1FDTD基本原理 ◆Yee的差分格式 Ex展开点((n+1/2)At(i+1/2)△x,jy,k)→(4.13) f-c小a >y展开点(n+1At,iax0+1/2)△y.k△z)→(4.14) 小时L“ro封 >Ez展开点((n+1/2)△t,ix,j4y.(k+1/2)△z)→(4.15) ea听ua生 6
6 4.1 FDTD基本原理 Yee的差分格式 Ex展开点((n+1/2)t, (i+1/2)x, jy, kz) (4.13) Ey展开点((n+1/)t, ix, (j+1/2)y, kz) (4.14) Ez展开点((n+1/2)t, ix, jy,(k+1/2)z) (4.15) 1 1 1 1 2 2 2 2 1 ,1 ,2 1 1 1 1 1 1 1 1 , , , , , , , , 1 1 2 2 2 2 2 2 2 2 , , , , + 2 2 n n n n z z y y n n x Ex x Ex H i j k H i j k H i j k H i j k E i j k C E i j k C y z 1 1 1 1 2 2 2 2 1 ,1 ,2 1 1 1 1 1 1 1 1 , , , , , , , , 1 1 2 2 2 2 2 2 2 2 , , , , + 2 2 n n n n x x z z n n y Ey y Ey H i j k H i j k H i j k H i j k E i j k C E i j k C z x 1 1 1 1 2 2 2 2 1 ,1 ,2 1 1 1 1 1 1 1 1 , , , , , , , , 1 1 2 2 2 2 2 2 2 2 , , , , + 2 2 n n n n y y x x n n z Ez z Ez H i j k H i j k H i j k H i j k E i j k C E i j k C x y
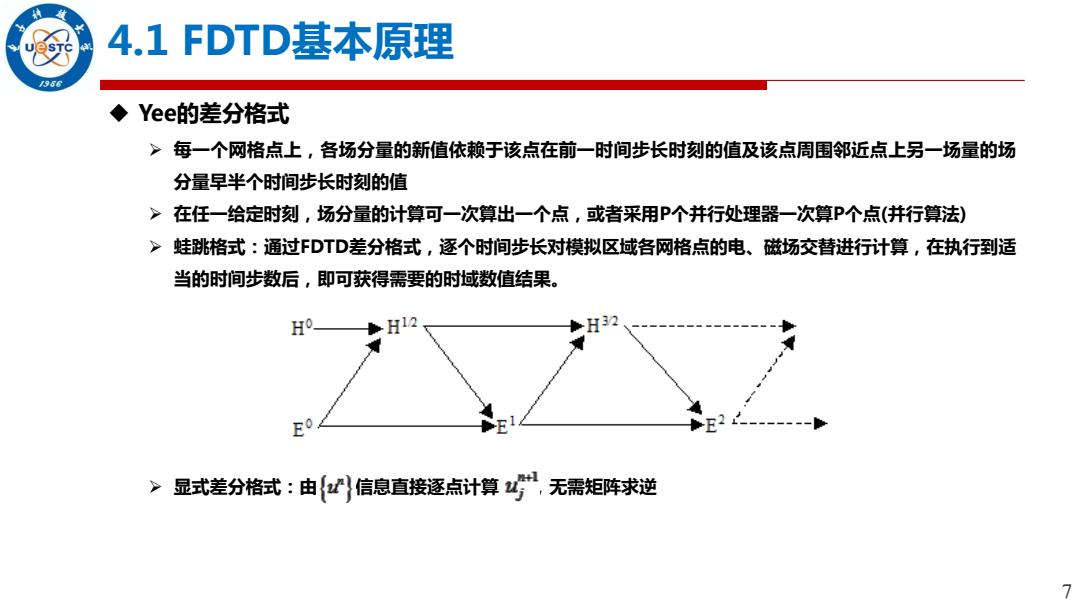
4.1FDTD基本原理 ◆ Yee的差分格式 >每一个网格点上,各场分量的新值依赖于该点在前一时间步长时刻的值及该点周围邻近点上另一场量的场 分量早半个时间步长时刻的值 >在任一给定时刻,场分量的计算可一次算出一个点,或者采用P个并行处理器一次算P个点(并行算法) >蛙跳格式:通过FDTD差分格式,逐个时间步长对模拟区域各网格点的电、磁场交替进行计算,在执行到适 当的时间步数后,即可获得需要的时域数值结果。 HO. H12 30 >显式差分格式:由{信息直接逐点计算,无需矩阵求逆 7
7 4.1 FDTD基本原理 Yee的差分格式 每一个网格点上,各场分量的新值依赖于该点在前一时间步长时刻的值及该点周围邻近点上另一场量的场 分量早半个时间步长时刻的值 在任一给定时刻,场分量的计算可一次算出一个点,或者采用P个并行处理器一次算P个点(并行算法) 蛙跳格式:通过FDTD差分格式,逐个时间步长对模拟区域各网格点的电、磁场交替进行计算,在执行到适 当的时间步数后,即可获得需要的时域数值结果。 显式差分格式:由 信息直接逐点计算 ,无需矩阵求逆

4.1FDTD基本原理 956 环路积分解释 >积分形式的时域麦克斯韦方程:安培定律和法拉第定律 H 6+k+ 安培定律 E 环路C (,j,k+ ■场量在环路每一边中点的值等于场量在该边的平均值 H 右边=(一+A+H(+分k+4 -++》-,-+}y气e i-,k+ ■E,k+ 等于Ez在小面元S1的平均值:时间中点取在(n+1/2)△t 东边=+引别 fa-生- 2k+ 2k+2 8
8 4.1 FDTD基本原理 环路积分解释 积分形式的时域麦克斯韦方程:安培定律和法拉第定律 安培定律: 场量在环路每一边中点的值等于场量在该边的平均值 等于Ez在小面元S1的平均值; 时间中点取在(n+1/2)t 1 1 1 1 S C d d t D S H l 环路 E i j k z , , 1 2 0 1 1 1 , , , , 2 2 n n z z x y E i j k E i j k t 左边 1 1 1 1 2 2 2 2 1 0 1 1 1 1 1 1 1 1 , , , , , , , , 1 1 2 2 2 2 2 2 2 2 , , , , 2 2 n n n n yyxx n n z z H i j k H i j k H i j k H i j k t E i j k E i j k x y 1 1 1 1 , , , , 2 2 2 2 1 1 1 1 , , , , 2 2 2 2 x y x y H i j k x H i j k y H i j k x H i j k y 右边 H x 1 1 ( , , ) 2 2 i j k H x 1 1 ( , , ) 2 2 i j k H y H y 1 1 ( , , ) 2 2 i j k 1 1 ( , , ) 2 2 i j k x y z E y E y 1 ( , , ) 2 i j k 1 ( , , 1) 2 i j k E z 1 ( , , ) 2 i j k E z 1 ( , 1, ) 2 i j k C1 1 S

4.1FDTD基本原理 966 环路积分解释 +1+ >积分形式的时域麦克斯韦方程:安培定律和法拉第定律 E 法拉第定律: (i+ 环路C E ■场量在环路每一边中点的值等于场量在该边的平均值 H 右边=-+2-E(+l1+2Ay 5,j+1k +++E(*小 H++人等于Hz在小面元S2的平均值;时间中点取在nAt 另一条获得差分格式的途径 可将环路路径选取来与弯曲表 左边:(++小(++ 面、槽缝等结构共形相配 tic -E;
9 4.1 FDTD基本原理 环路积分解释 积分形式的时域麦克斯韦方程:安培定律和法拉第定律 法拉第定律: 场量在环路每一边中点的值等于场量在该边的平均值 等于Hz在小面元S2的平均值; 时间中点取在 nt 2 2 2 2 S C d d t B S E l 环路 1 1 , , 1, , 2 2 1 1 , 1, , , 2 2 x y x y E i j k x E i j k y E i j k x E i j k y 右边 1 1 , , 2 2 H i j k z 1 1 0 2 2 1 1 1 1 , , , , 2 2 2 2 n n z z x y H i j k H i j k t 左边 1 1 2 2 0 1 1 1 1 , 1, , , , , 1, , 1 1 1 1 2 2 2 2 , , , , 2 2 2 2 n n n n x x y y n n z z E i j k E i j k E i j k E i j k t H i j k H i j k y x E x 1 ( , , ) 2 i j k E x 1 1 ( , 1, ) 2 2 i j k H y H y 1 ( , , ) 2 i j k 1 ( 1, , ) 2 i j k x y E y z E y 1 1 ( , 1, ) 2 2 i j k H z 1 1 ( , , ) 2 2 i j k H z C2 1 ( , 1, ) 2 i j k 1 3 ( , , ) 2 2 i j k 2 S 另一条获得差分格式的途径 可将环路路径选取来与弯曲表 面、槽缝等结构共形相配

4.2解的稳定性条件 956 ◆不稳定性表现:随着时间步数的增加,计算结果将无限制地增加 ◆稳定性条件:△t和X、△y和△z必须满足一定的关系 ◆稳定性条件推导思路 >任何波都能展开为平面波谱的迭加 >考察算法对一平面波是否稳定 >把有限差分算式分解为时间本征值问题和空间本征值问题 >将平面波本征模带入空间本征值方程→本征值入 >入应在由时间本征值方程确定的稳定区间 10
10 4.2 解的稳定性条件 不稳定性表现:随着时间步数的增加,计算结果将无限制地增加 稳定性条件:t和x、y和z必须满足一定的关系 稳定性条件推导思路 任何波都能展开为平面波谱的迭加 考察算法对一平面波是否稳定 把有限差分算式分解为时间本征值问题和空间本征值问题 将平面波本征模带入空间本征值方程本征值 应在由时间本征值方程确定的稳定区间

4.2解的稳定性条件 ◆稳定性条件推导 △x △y 好*.**u.*w+ △i △y >方程左边可构成各相应场分量的时间本征值方程;方程右边可构成同本征值的空间本征值方程 吃-v 左边(时间微分)= =V”=右边(空间微分) △t 时间本征值问题空间本征值问题 11
11 4.2 解的稳定性条件 稳定性条件推导 方程左边可构成各相应场分量的时间本征值方程; 方程右边可构成同本征值的空间本征值方程 左边(时间微分)= =右边(空间微分) 时间本征值问题 空间本征值问题 1 1 1 1 1 2 2 2 2 1 1 1 1 1 1 1 1 1 1 , , , , , , , , , , , , 2 2 2 2 2 2 2 2 2 2 1 n n n n n n E i j k E i j k H i j k H i j k H i j k H i j k z z y y x x t x y 1 1 2 2 1 1 1 1 1 1 1 1 , , , , 1, , , , , 1, , , 2 2 2 2 2 2 2 2 1 n n n n n n H i j k H i j k E i j k E i j k E i j k E i j k z z y y x x t x y 1 1 2 2 n n V V n V t