计算电磁学 (小班研讨课) 966 第九章空域差分-时域矩量法 目 录 2
2 计算电磁学(小班研讨课) 目 录 第九章 空域差分-时域矩量法
966 I传统FDTD法 >数值色散 结构特点、电磁特性等 网格大小 时间稳定性条件 > 网格大小 时间步长 Q1:什么是多尺度结构?为什么FDTD 计算多尺度问题的困难很大? 口无条件稳定ADI-FDTD、LOD-FDTD等 Q2:计算同一种问题,ADI-FDTD的计 算速度是否一定比FDTD快? >理论上无条件稳定(时间步长取很大) > 数值色散误差影响,时间步长取值受到限制 ▣ 空域差分-时域矩量法(space-domain finite-difference and time-.domain moment,.SDFD-TDM) >差分方法处理空间域,按矩量法过程处理时间域 >不同的基函数和检验过程处理时间变量,可以得到不同的计算格式 3
3 传统FDTD法 ➢ 数值色散、结构特点、电磁特性等 网格大小 ➢ 网格大小 时间步长 无条件稳定ADI-FDTD、LOD-FDTD等 ➢ 理论上无条件稳定(时间步长取很大) ➢ 数值色散误差影响,时间步长取值受到限制 空域差分-时域矩量法(space-domain finite-difference and time-domain moment, SDFD-TDM) ➢ 差分方法处理空间域,按矩量法过程处理时间域 ➢ 不同的基函数和检验过程处理时间变量,可以得到不同的计算格式 时间稳定性条件 Q1:什么是多尺度结构?为什么FDTD 计算多尺度问题的困难很大? Q2:计算同一种问题,ADI-FDTD的计 算速度是否一定比FDTD快?

9.1空域差分-时域矩量法 966 9.1空域差分-时域矩量法 9.1.1空域差分-时域矩量法的基本原理 有源区域,媒质参数不随时间变化且各向同性,时域Maxwel差分方程 E,(r,t)1 8t &(r) aH.(.n_oH.(D-()E.(.)-J.(. ay 02 (1) OH,(r,t)1 E,(r,t)E.(r,t) Ot (r) 0z 用已知的基函数g,()和h,(1)分别对电场、磁场进行展开 Ec,0=∑E(r)g.( n=( 求解对象 Hr,0=∑b@ (2) Q:这两个展开式中有什么特点?
4 9.1 空域差分-时域矩量法 9.1 空域差分-时域矩量法 9.1.1 空域差分-时域矩量法的基本原理 有源区域,媒质参数不随时间变化且各向同性,时域Maxwell差分方程 ( , ) 1 ( , ) ( , ) ( ) ( , ) ( , ) ( ) x z y x x E t H t H t E t J t t y z = − − − r r r r r r r 用已知的基函数gn (t)和hn (t)分别对电场、磁场进行展开 ( , ) 1 ( , ) ( , ) ( ) x y z H t E t E t t z y = − r r r r , , , , 0 ( , ) ( ) ( ) n x y z x y z n n E t E g t = r r = , , , , 0 ( , ) ( ) ( ) n x y z x y z n n H t H h t = r r = 求解对象 Q:这两个展开式中有什么特点? (1) (2)

9.1空域差分-时域矩量法 1966 (2)代入(1),得 ∑E31 aH"(r)_oH"(r) n= (r)0 (r)mo 2号 (3) n= 在方程(3)的两边同时乘以权函数w,m(),并在区间t∈(-o,o)上对t积分,可得 Q:引入权函数求 内积的目的? 22o&0r.0地Je0地 20a-名d留 E"(r) L.m..0 时域解析处理
5 9.1 空域差分-时域矩量法 0 0 0 ( ) 1 ( ) 1 ( ) ( ) ( ) ( ) ( ) ( ) ( , ) ( ) ( ) ( ) n n n n n z y x n x n x n n n g t H H E h t E g t J t t y z = = = = − − − r r r r r r r r r (2)代入(1),得 0 0 ( ) 1 ( ) ( ) ( ) ( ) ( ) n n n n y z x n n n h t E E H g t t z y = = = − r r r r (3) 在方程(3)的两边同时乘以权函数wm (t),并在区间t∈(-∞, ∞)上对 t 积分,可得 ( ) ( ) ( ) ( ) 0 0 0 ( ) 1 ( ) ( ) ( ) d ( ) d ( ) ( ) 1 ( ) ( ) d ( , ) d ( ) ( ) n n n n z y x m n m n n n x n m x m n g t H H E w t t h t w t t t y z E g t w t t J t w t t + + − − = = + + − − = = − − − r r r r r r r r r ( ) ( ) 0 0 ( ) 1 ( ) ( ) ( ) d ( ) d ( ) n n n n y z x m n m n n h t E E H w t t g t w t t t z y + + − − = = = − r r r r (4) 时域解析处理 Q:引入权函数求 内积的目的?

9.1空域差分-时域矩量法 1966 从空域差分-时域矩量法体系推导FDTD法 选取分域三角基函数T,(t)展开时域电磁场分量 E-(r,)=∑E(r)T(t) (5) H(r,)=∑H-(r)T(0 (t-1)/(tn-t),tEt) 其中,Tn()=n+1-t)(nH-tn)t∈[n,ti] 0, 其他 (5)代入(4),且采用点匹配法作为权函数 电场方程:0=-(a+引 磁场方程: wn(t)=6(t-m△t) 6
6 9.1 空域差分-时域矩量法 从空域差分-时域矩量法体系推导FDTD法 选取分域三角基函数Tn (t)展开时域电磁场分量 , , , , ( ) ( ) ( ) n x y z x y z n n E ,t = E T t r r , , , , ( ) ( ) ( ) n x y z x y z n n H ,t = H T t r r 1 1 1 1 1 1 ( ) /( ), [ , ) ( ) ( ) /( ), [ , ] 0, n n n n n n n n n n n t t t t t t t T t t t t t t t t − − − + + + − − = − − 其他 (5) 其中, (5)代入(4),且采用点匹配法作为权函数 电场方程: 磁场方程: 1 ( ) 2 w t t m t m = − + ( ) ( ) w t t m t m = −

9.1空域差分-时域矩量法 9656 E(r)-E(r)_1 OH.(r) OH""(r) o(r △t E(r Cy 0z E(r e( H)-H) 1 OE"(r)E"(r) Yee氏网格和中心差分处理 △t u(r)dz 8y 标准FDTD步进公式 E 小结:FDTD法是SDFD-TDM法的一种特殊情况,可以从时域选取分域三角基 函数和点匹配法得到。 7
7 9.1 空域差分-时域矩量法 1 1 1 2 2 1 1 2 2 ( ) ( ) 1 ( ) ( ) 1 ( ) ( ) ( ) ( ) ( ) ( ) m m m m m m x x z y x x E E H H E J t y z + + + + + − = − − − r r r r r r r r r r 1 1 2 2 ( ) ( ) 1 ( ) ( ) ( ) m m m m x x y z H H E E t z y + − − = − r r r r r 小结:FDTD法是SDFD-TDM法的一种特殊情况,可以从时域选取分域三角基 函数和点匹配法得到。 Yee氏网格和中心差分处理 标准FDTD步进公式 E H

9.1空域差分-时域矩量法 956 9.1.2基于分域三角基函数和Galerkin法的SDFD-TDM法 简单、无耗媒质中TE波有E、E,和H,三个场分量存在。电磁场分量的时间变化 用分域三角基函数T(t)展开 {E,E,H.(,)}=∑{E,E,H(r)T 代入二维TE波的Maxwellf微分方程中,得 证.0.1aa0r,0- J(r,t) 1=1 ()石 y a(r) 立o020)- E(r) (6) 2() 8
8 9.1.2 基于分域三角基函数和Galerkin法的SDFD-TDM法 9.1 空域差分-时域矩量法 简单、无耗媒质中TEz波有Ex、Ey和Hz三个场分量存在。电磁场分量的时间变化 用分域三角基函数Tn (t)展开 1 , , ( , ) , , ( ) ( ) n n n x y z x y z n n E E H t E E H T t = r r = 代入二维TEz波的Maxwell微分方程中,得 ( ) ( ) ( ) ( ) ( ) 1 1 ( ) 1 ( , ) n n n z x x n n n T t H J t E T t t y = = = − r r r r r ( ) ( ) ( ) ( ) ( ) 1 1 ( ) 1 , n n n z y y n n n T t H J t E T t t x = = − = − r r r r ( ) ( ) ( ) ( ) ( ) ( ) 1 1 1 n n n n x y z n n n T t E E H T t t y x = = = − r r r r (6)

9.1空域差分-时域矩量法 为消去含时间变量的T,(),根据Galerkin方法,在方程(6)的两边同时乘以Tm(t), 并在区间1∈[0,o)上对t进行积分,得到 r(T(( (r) 2290a-2z0g.0ag0a (7) E(r)ax OE2(r)_ r.or.0地 整数N代替无穷大o” 9
9 9.1 空域差分-时域矩量法 为消去含时间变量的Tn (t),根据Galerkin方法,在方程(6) 的两边同时乘以Tm (t), 并在区间 t ∈ [0, ∞)上对 t 进行积分,得到 0 0 0 1 1 ( ) 1 1 ( ) ( ) ( )d ( ) ( )d ( , ) ( )d ( ) ( ) n n n z x m n m x m n n T t H E T t t T t T t t J t T t t t y = = = − r r r r r 0 0 0 1 1 ( ) 1 1 ( ) ( ) ( )d ( ) ( )d ( , ) ( )d ( ) ( ) n n n z y m n m y m n n T t H E T t t T t T t t J t T t t t x = = − = − r r r r r 0 0 1 1 ( ) ( ) 1 ( ) ( ) ( )d ( ) ( )d ( ) n n n n x y z m n m n n T t E E H T t t T t T t t t y x = = = − r r r r (7) 整数“N”代替无穷大“∞
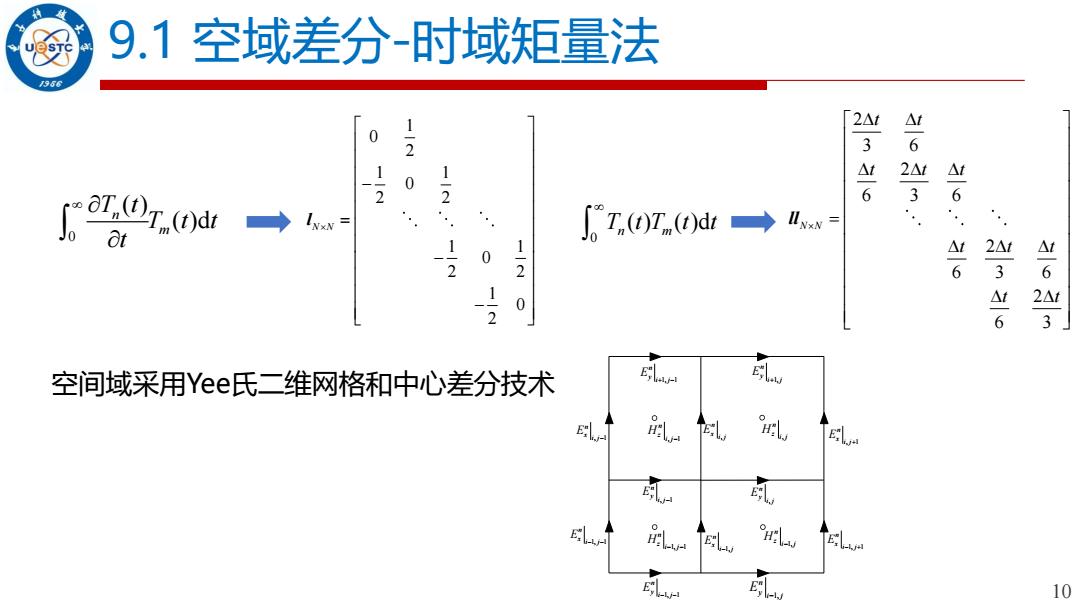
9.1空域差分-时域矩量法 966 1-2 46 1 2 0 1-2 46 6 I,07(0d 0 1-2 g 0 4346 空间域采用Yee氏二维网格和中心差分技术 E 10
10 9.1 空域差分-时域矩量法 0 ( ) ( )d n m T t T t t t 1 0 2 1 1 0 2 2 1 1 0 2 2 1 0 2 N N − = − − l 0 ( ) ( )d T t T t t n m 2 3 6 2 6 3 6 2 6 3 6 2 6 3 N N t t t t t t t t t t = ll 空间域采用Yee氏二维网格和中心差分技术 , n x i j E , n y i j E 1, n x i j E − , 1 n x i j E − , 1 n x i j E + 1, 1 n x i j E − − 1, 1 n x i j E − + 1, n y i j E − , 1 n y i j E − 1, 1 n y i j E − − 1, 1 n y i j E + − 1, n y i j E + , n z i j H 1, n z i j H − 1, 1 n z i j H − − , 1 n z i j H −

9.1空域差分-时域矩量法 956 方程(7)进行差分离散: ...o [l,l+,-H帆l,ug.0u 4[l是y[以,l是[g,吼,l 可以消去磁场分量 Q:矩阵计算中消去磁场分量的优点和缺点? 11
11 9.1 空域差分-时域矩量法 方程(7)进行差分离散: , , , 1 0 1 1 , , 1 1 ( , ) ( )d n n n N N N N x z z x m i j i j i j N N i j j i j N E H H J t T t t y − − − − = ll l r , , 1, 0 1 1 , , 1 1 ( , ) ( )d n n n N N N N y z z y m i j i j i j N N i j i i j N E H H J t T t t x − − + − = ll l r , , 1 , 1, , 1 1 1 , , n n n n n N N N N N N z x x y y i j i j i j i j i j N N N i j j i j i H E E E E y x + + = − − − ll ll l 可以消去磁场分量 Q:矩阵计算中消去磁场分量的优点和缺点?