
第一章物质磁性概述 第一节基本磁学量 第二节磁化状态下磁体中的静磁能量 第三节物质按磁性分类 第四节 磁性材料的磁化曲线和磁滞回线 返回 放映结束
第一节 基本磁学量 第二节 磁化状态下磁体中的静磁能量 第三节 物质按磁性分类 第四节 磁性材料的磁化曲线和磁滞回线 返回 放 映 结 束 第一章 物质磁性概述
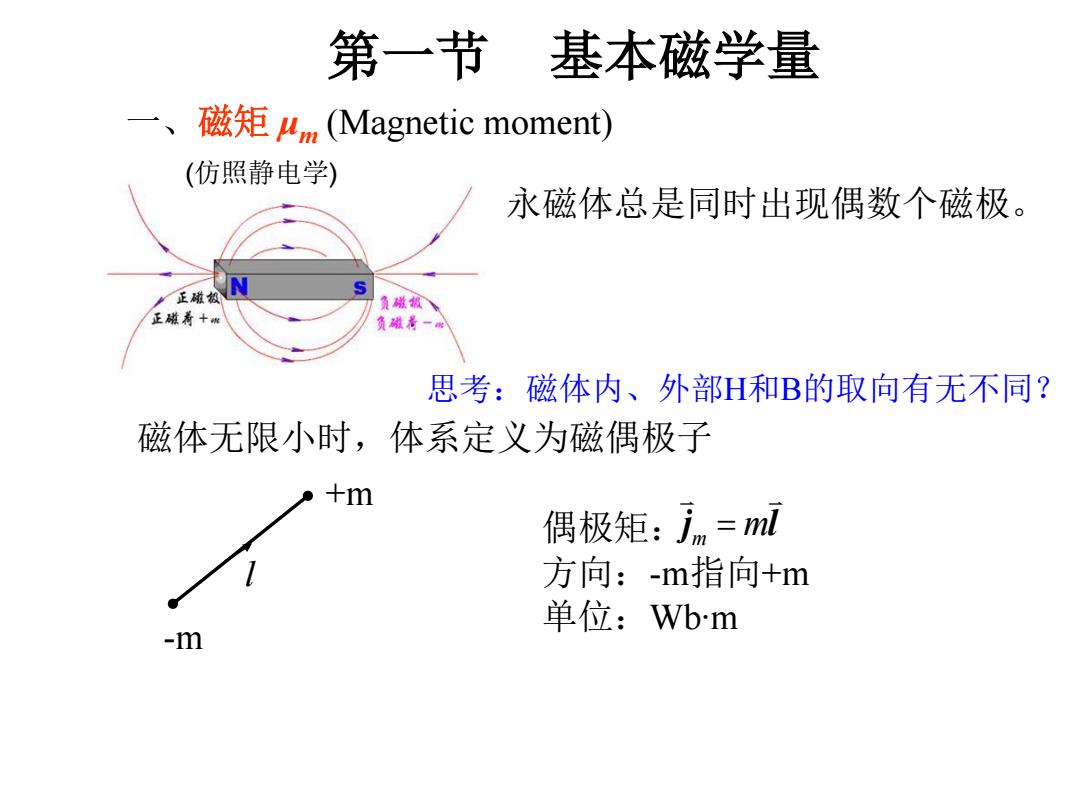
第一节 基本磁学量 一、1 磁矩4m(Magnetic moment) (仿照静电学) 永磁体总是同时出现偶数个磁极。 正嫩极 负磁敏 正磁着十w 负磁考一四 思考:磁体内、外部H和B的取向有无不同? 磁体无限小时,体系定义为磁偶极子 +m 偶极矩:jm=mld 方向:-m指向+m 单位:Wbm m
一、磁矩 μm (Magnetic moment) 永磁体总是同时出现偶数个磁极。 磁体无限小时,体系定义为磁偶极子 偶极矩: 方向:-m指向+m 单位:Wb∙m j l m m +m -m l 第一节 基本磁学量 思考:磁体内、外部H和B的取向有无不同? (仿照静电学)

用环形电流描述磁偶极子: 面积 磁矩:心m=iA单位:Am2 二者的物理意义: 表征磁偶极子磁性强弱与方向 jm Mom (电流 4。=4π×10-7H.m 电子的轨道运动相当于一个恒定的电流回路,必 有一个磁矩(轨道磁矩),但自旋也会产生磁矩(自 旋磁矩),自旋磁矩是基本粒子的固有磁矩
用环形电流描述磁偶极子: 磁矩: 单位:A ∙m2 二者的物理意义: 表征磁偶极子磁性强弱与方向 μ A m i 7 1 0 4 10 H m - o m μm j 电子的轨道运动相当于一个恒定的电流回路,必 有一个磁矩(轨道磁矩),但自旋也会产生磁矩(自 旋磁矩),自旋磁矩是基本粒子的固有磁矩

磁单极子 1931年,英国物理学家P.A.M狄拉克利用数学公式预言了磁单极子存在于携 带磁场的管(狄拉克弦)的末端。 美国科学家用同步回旋加速器,多次用高能质子与轻原子核碰撞,但依旧无 磁单极子产生的迹象。 美国科学家转而致力于能量更大的天然宇宙射线(1、宇宙射线本身可能含 有磁单极子;2、宇宙射线粒子与高空大气原子、离子、分子等碰撞会产生 磁单极子),未果。 1982年,美国凯布雷拉采用超导量子干涉器件磁强计,进行了151天观察记 录,经周密分析,认为磁单极子穿过了超导线圈,但未能重复观察到。不足 以肯定其存在。 中国、瑞士、日本多国科学家联合小组报告发现了磁单极子存在的间接证据, 在一种铁磁晶体中观察到反常霍尔效应,且认为只有假设存在磁单极子才能 解释这种现象。 2009.09.03,科学杂志。德国亥姆霍兹联合会研究中心D.J.P.Morris等在自 旋冰Dy2T,O,晶体(烧录石晶格)中进行中子散射,对晶体施加一个磁场, 影响弦的对称和方向,从而降低弦网络的密度以促成单极子的分离。结果, 在0.6K到2K温度条件下,这些弦是可见的,并在其两端出现了磁单极子
磁单极子 1931年,英国物理学家P.A.M狄拉克利用数学公式预言了磁单极子存在于携 带磁场的管(狄拉克弦)的末端。 1982年,美国凯布雷拉采用超导量子干涉器件磁强计,进行了151天观察记 录,经周密分析,认为磁单极子穿过了超导线圈,但未能重复观察到。不足 以肯定其存在。 美国科学家用同步回旋加速器,多次用高能质子与轻原子核碰撞,但依旧无 磁单极子产生的迹象。 美国科学家转而致力于能量更大的天然宇宙射线(1、宇宙射线本身可能含 有磁单极子;2、宇宙射线粒子与高空大气原子、离子、分子等碰撞会产生 磁单极子),未果。 中国、瑞士、日本多国科学家联合小组报告发现了磁单极子存在的间接证据, 在一种铁磁晶体中观察到反常霍尔效应,且认为只有假设存在磁单极子才能 解释这种现象。 2009.09.03,科学杂志。德国亥姆霍兹联合会研究中心D.J.P.Morris等在自 旋冰Dy2Ti2O7晶体(烧录石晶格)中进行中子散射,对晶体施加一个磁场, 影响弦的对称和方向,从而降低弦网络的密度以促成单极子的分离。结果, 在0.6K到2K温度条件下,这些弦是可见的,并在其两端出现了磁单极子

二、磁化强度M(magnetization) (描述宏观磁体磁性强弱程度) 单位体积的磁体内,所有磁偶极矩的jm或 磁矩4m的矢量和,分别为: 磁极化强度:了= 10wb-m2) △/ 磁化强度:M=∑(Am Λ/ .jm =Hom .J=4,M 二者物理意义:描述磁体被磁化的方向与强度
二、磁化强度 M (magnetization) (描述宏观磁体磁性强弱程度) 单位体积的磁体内,所有磁偶极矩的 jm或 磁矩μm的矢量和 ,分别为: 磁极化强度: ( ) 2 Wb m V m j J 磁 化 强 度: (A m ) 1 V μm M j J M m 0 μm 0 二者物理意义:描述磁体被磁化的方向与强度

比磁化强度σ:单位质量磁体内具有的磁矩矢量和。 a∑,=k0 6= emu/g(CGS) 1A·m2.kg=lemu/g 三、磁场强度H与磁感应强度B 均为描述空间任意一点的磁场参量(矢量) 1、H:静磁学定义为单位点磁荷在该处所受的磁场 力的大小,方向与正磁荷在该处所受磁场力方向一致。 月=F,F=k.m业元,其中k= m 4W0 specific magnetization H magnetic field B magnetic flux density
比磁化强度σ:单位质量磁体内具有的磁矩矢量和。 三、磁场强度 H 与磁感应强度 B 均为描述空间任意一点的磁场参量(矢量) 1、H :静磁学定义 H为单位点磁荷在该处所受的磁场 力的大小,方向与正磁荷在该处所受磁场力方向一致。 0 3 1 2 4 1 , , r k r m m F k m F H 其中 1A m kg 1emu/g emu/g(CGS) A m kg (SI) / 1 2 -1 2 -1 d Vd M μm σ specific magnetization H magnetic field B magnetic flux density
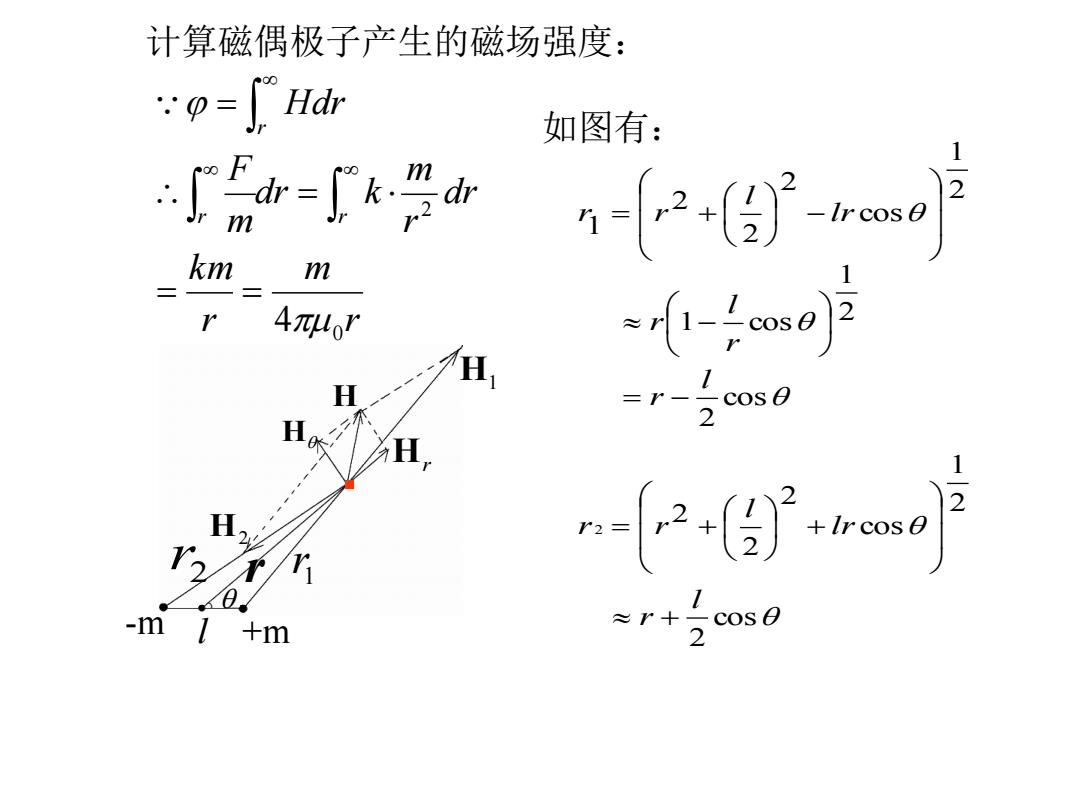
计算磁偶极子产生的磁场强度: Hdr 如图有: 「-e-- m km m r 4πo' smo) H -m +m =r+
计算磁偶极子产生的磁场强度: 如图有: cos 2 2 1 cos 2 2 2 cos 2 2 1 1 cos 2 1 cos 2 2 2 1 2 l r lr l r r l r r l r lr l r r r m r k m dr r m dr k m F Hdr r r r 0 2 4 H H Hr H1 H2 1 r 2 r r -m l +m ·

磁位势: m 0=9+01=445 -m 4π4o'2 m 1 1 m 1 1 AnLo 1 cos0 1cos0 1cos0 r+ 44 1+ 2 2 2r ml cos0 ml cos0 44 2 1- 44r1 jm cos 91f 442 ATuo 3
磁位势: 3 0 2 0 2 2 0 2 2 2 0 0 0 0 1 0 2 1 2 4 1 4 cos cos 4 cos 4 1 cos 4 2 cos 1 1 2 cos 1 1 4 2 cos 1 2 cos 1 4 . 4 4 r r j r m l r r l m l r l r r l m l r l r m r m r m m m j r

-ve- t小a小 派 H沿r方向及使0角增加方向的分量计算: 在球坐标系中:V=, +e a∂ 1a 1∂ ∂r o r 80
3 5 0 3 4 0 3 3 0 3 0 3 4 1 3 4 1 1 1 4 1 4 r r r j r r j r r r H m m m m m m m j r j r j r j r j r H沿r 方向及使θ 角增加方向的分量计算: sin 1 1 r e r e r er 在球坐标系中:
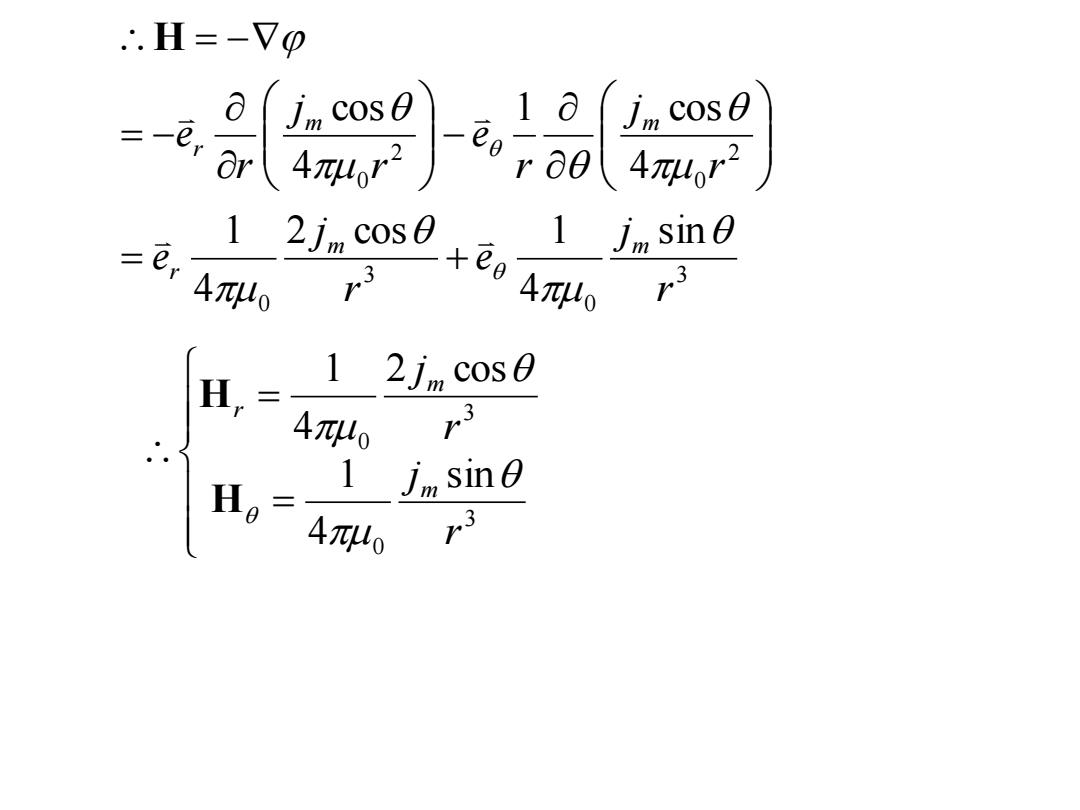
.H=-70 -e8,a】 1 2jm cose 二,4wo 1 jm sine +Ee4πlo H,= 1 2jm cos0 4π4o 1 jm sine Hg=4π40 r3
3 0 3 0 2 0 2 0 sin 4 2 cos 1 4 1 4 1 cos 4 cos r j e r j e r j r e r j r e m m r m m r H 3 0 3 0 sin 4 1 2 cos 4 1 r j r j m m r H H