
导波场论 回顾上次: 位函数法(赫兹磁位函数) 电磁波波型正交性 波的传播特性 波的功率流 本次课程: 凋落波的能量 波导的损耗(难点)
导 波 场 论 回顾上次: 位函数法(赫兹磁位函数) 电磁波波型正交性 波的传播特性 波的功率流 本次课程: 凋落波的能量 波导的损耗(难点)

导波场论 回顾分离变量法一位函数法 利用赫兹磁矢量求解H波(TE波)的电磁场 Vy(g,92)+(k2+Y9,4)=0 由纵 型与H,就有相 边 同的边界条件 界条件 时空分离 纵横分离 变量分离 解织向场分量 向分求 量 量 求解亚、y或K。 = (k2+y2)w(q,92)eo- 由亚求解出电磁场 E,=+joui:×V,Πnmeo H,=-V,w(,92)eo- E波(TH波)电磁场求解 磁赫电矢量(中、E,)
导 波 场 论 回顾 分离变量法——位函数法 利用赫兹磁矢量求解H波(TE波)的电磁场 Ψ与Hz就有相 同的边界条件 由Ψ求解出电磁场 求解Ψ、γ或Kc 边 界 条 件 E波(TH波)电磁场求解——磁赫电矢量 (φ、Ez) 2 2 2 1 2 1 2 ( , ) ( ) ( , ) 0 t q q k q q 2 2 1 2 1 2 ( ) ( , ) ( , ) j t z z j t t z t mz j t z t t H k q q e E j i e H q q e 时 空 分 离 纵 横 分 离 变 量 分 离 求 解 纵 向 场 分 量 由纵 向场 分量 求解 横向 场分 量
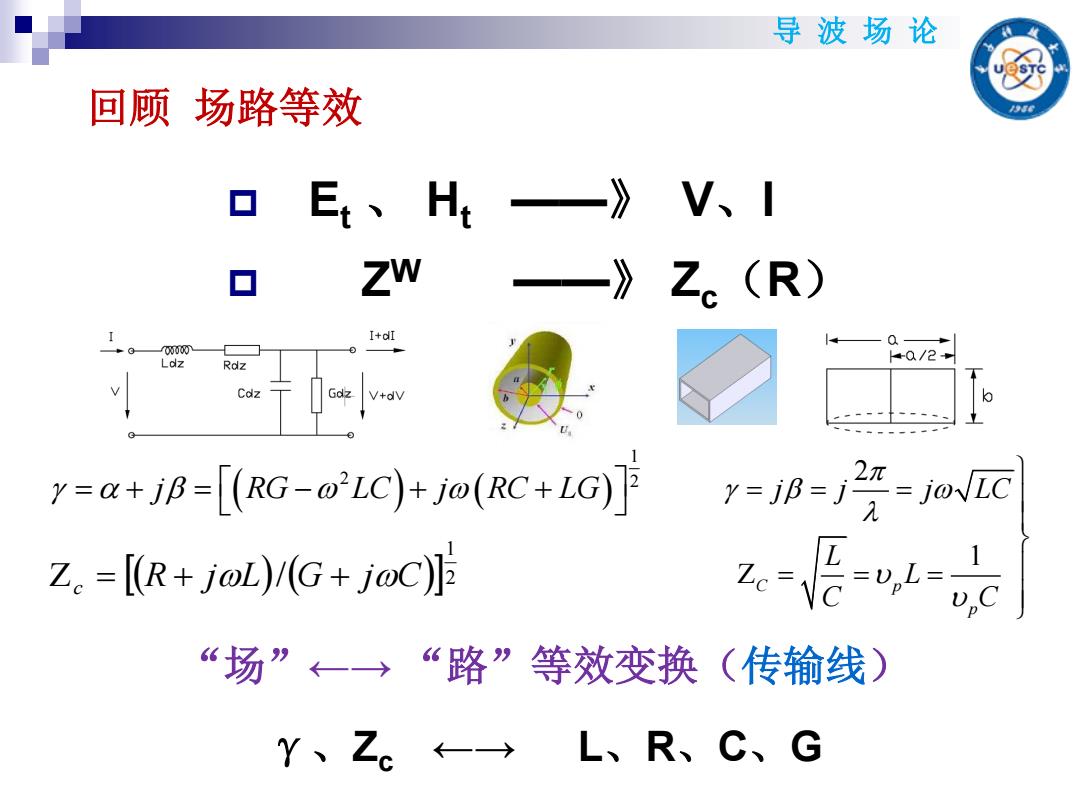
导波场论 回顾场路等效 ▣ Et、Ht 》V、1 ▣ Zw —》Z。(R) I+dI 一00000 +0/2+ Ldz Rdz Coz Gdz V+dV y-q+jB=[(RG-@'LC)+j@(RC+LG)i y=j形=2经=jo风 Z。=[【(R+joL)/G+joC z-== “场”←一→“路”等效变换(传输线) Y、Z- L、R、C、G
导 波 场 论 回顾 场路等效 Et 、 Ht ——》 V、I ZW ——》 Zc(R) “场”←→ “路”等效变换(传输线) γ、Zc ←→ L、R、C、G 1 2 2 j RG LC j RC LG 2 1 c R jL / G jC 2 1 C p p j j j LC L L C C

导波场论 回顾电磁波波型正交性 ∬/×f=0 ∬ff=0 S 1、基于亥姆霍兹方程 V2f+k2f=0 Uf+所=0ff-f=- fvif +kafif =0 →(-∬ff,=j(f,-fvf)→(-)川,w=0 同过程: 叮4可,w=0∬×y,)小×y,=0 ∬瓦×可,y,)可,=0
导 波 场 论 回顾 电磁波波型正交性 0 i j s f f ds 0 i j v f f dv 1、基于亥姆霍兹方程 2 2 2 2 0 0 j t i ci i j i t j cj i j f f k f f f f k f f 2 2 0 t c f k f 2 2 2 2 ( ) j t i i t j j i i j f f f f f f 2 2 2 2 ( ) i j i j i t j j t i v v f f dv f f f f dv 2 2 ( ) 0 i j i j v f f dv i t j 0 v dv ( ) ( ) 0 z i z j v i i dv ( ) 0 z t j t i v i dv 同过程:

导波场论 回顾电磁波波型正交性 川f,×,ds=0 川f所,=0 2、基于麦氏方程 ×E=-j0uF→.(En×H-En×Hn)=0 ∬i-(e×h-en×h,)d=0 →J∫i.·(En×H-Em×Hm)s=0→ ∬(-ex瓦-e×)ds=0 ∬i.(e,×hn)s=0 同过程: ∬-(e,×h)s=0 (e。×h,)d=0 ∬2(e×)
导 波 场 论 回顾 电磁波波型正交性 0 i j s f f ds 0 i j v f f dv 2、基于麦氏方程 E j H ( ) 0 E H E H n m m n z tn tm tm tn ( ) 0 s i E H E H ds ( ) 0 ( ) 0 z n m m n s z n m m n s i e h e h ds i e h e h ds ( ) 0 ( ) 0 z n m s z m n s i e h ds i e h ds 同过程: * * ( ) 0 ( ) z n m s z m n s i e h ds i e h ds

导波场论 回顾电磁波波型正交性 (1)纵场正交 (2)横场正交 储能正交 (3)模式之间正交 (4)功率正交 功率正交 (5)模式函数正交 在无耗导波系统中,一个波型与另一个波型之间的场不构成功率流,波 型之间无功率交叉。波导中所通过的总功率流等于各单独波型功率流的和。 导波系统中不同的TE模式或TM模式,彼此之间不会形成能量流动,或者说 他们所含的电磁能量彼此不会发生耦合
导 波 场 论 回顾 电磁波波型正交性 (1)纵场正交 (2)横场正交 (3)模式之间正交 (4)功率正交 (5)模式函数正交 功率正交 储能正交 在无耗导波系统中,一个波型与另一个波型之间的场不构成功率流,波 型之间无功率交叉。波导中所通过的总功率流等于各单独波型功率流的和。 导波系统中不同的TE模式或TM模式,彼此之间不会形成能量流动,或者说 他们所含的电磁能量彼此不会发生耦合

导波场论 回顾波的传播特性与功率流 ()波的色散关系 Y2=k2-k2 =a-(2y-(64-(2)84 相速: dt (2)导波系统中的电磁储能 f>人化.-形-∬H-I=4叮E-E W=2W,=2W
导 波 场 论 回顾 波的传播特性与功率流 (1)波的色散关系 2 2 2 c k k 2 2 2 2 2 0 2 2 2 ( ) ( ) ( ) r r r r c f f k v C 相速: 0 2 / 1 ( ) r r p c dz c v dt (2)导波系统中的电磁储能 c f f : * * = 4 4 m e v v W W H H dv E E dv 2 2 W W W m e

导波场论 回顾波的传播特性与功率流 (3)功率流 P-qg是川EhP=29发7& P=g 群速=能速 P(瓦) V。(米秒) W(瓦秒米) 2 =V 相速
导 波 场 论 回顾 波的传播特性与功率流 (3)功率流 2 2 1 1 2 z c s P E ds k 2 2 1 1 2 z c s P H ds k P W v 1 g 群速=能速 P(瓦) W(瓦秒/米) Vg(米/秒) 2 p g c v v v 相速
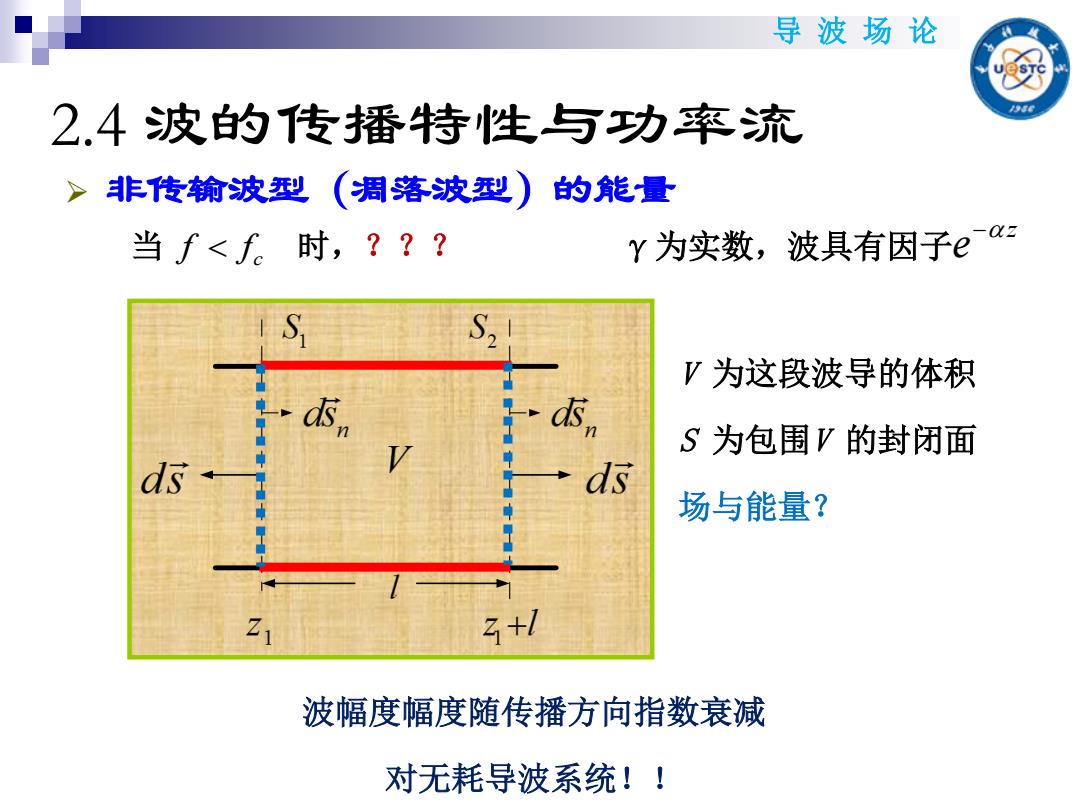
导波场论 2.4波的传播特性与功率流 非传输波型 (凋落波型) 的能量 当f<f。时,??? Y为实数,波具有因子ea S V为这段波导的体积 S为包围V的封闭面 ds ds 场与能量? 3+1 波幅度幅度随传播方向指数衰减 对无耗导波系统!!
导 波 场 论 波幅度幅度随传播方向指数衰减 对无耗导波系统!! 非传输波型(凋落波型)的能量 当 f f c 时,??? 2.4 波的传播特性与功率流 γ为实数,波具有因子 z e V 为这段波导的体积 S 为包围V 的封闭面 场与能量?

导波场论 由能流定理,及已经推导出得波导系统内的能量公式 ∬(E×H)s=-jo旷(H.f-sE.E)d ∬(ExH)-=-2y0m。-W.) Z+ 导波系统侧壁为电壁或磁壁 侧面无能量传输(?),故坡印庭矢量在侧面的积分为0; 有:2j(E×H)ds+2j医x瓦)i=2o。-,)
导 波 场 论 由能流定理,及已经推导出得波导系统内的能量公式 * * * ( ) ( ) s v E H ds j H H E E dv 1 * ( ) 2 ( ) 2 m e s E H ds j W W 1 2 1 1 * * ( ) + ( ) 2 ( ) 2 2 t t z t t z m e s s E H i ds E H i ds j W W 侧面无能量传输(?),故坡印庭矢量在侧面的积分为0; 导波系统侧壁为电壁或磁壁 有: