
导波场论 回顾上次: 纵向场解法举例 位函数法(赫兹电位函数) 本次课程: 位函数法(赫滋磁位函数) 电磁波波型正交性 波的传播特性 波的功率流
导 波 场 论 回顾上次: 纵向场解法举例 位函数法(赫兹电位函数) 本次课程: 位函数法(赫兹磁位函数) 电磁波波型正交性 波的传播特性 波的功率流

导波场论 回顾分离变量法一纵向场解法 以电场为例E(uy)=ReE(uy)e“ 时空分离 E(u,v,z) 纵横分离 E(u,v,z)=Er(u,v,z)+i-E:(u,v,z) 变量分离 E:(w,w,z)=E:(u,)Z(z) 求解纵向场分量 V2Ez+k2Ez =0:Z(Z)=A.e+B.etr= 由纵向场分量 求解横向场分量 ,E:,=VxE k2
导 波 场 论 回顾 分离变量法——纵向场解法 时空分离 . , , ; Re , , j t E u v z t E u v z e . . . E u v z E u v z i E u v z , , = , , , , T z z . E u v z , , . E u v z z , , T z T z 2 2 c c j E E H E k k ; 纵横分离 变量分离 求解纵向场分量 2 2 + Z 0 (z)=A e e z z t c Z E k E Z B ; 以电场为例 . = , z E u v Z z z 由纵向场分量 求解横向场分量

导波场论 回顾分离变量法一纵向场解法 E波(TM) H波(TE) 7E.+(k2+y2)E.=0 VH.+(k2+y2)H.=0 -Y 1 aE. -Y 1aH, Emke g 直角坐标系 Ha=kye og Ed: -Y 1 aE. 圆柱坐标系 -y1aH。 k2+y2e ∂q2 拉梅系数 Ha=kye:092 jos 1 aE. E4 -joa 1 6H. Hoky e2 0g2 k2+y2e20q2 10 :1 aH. -j081a∂E k2+y2 e Oqi
导 波 场 论 回顾 分离变量法——纵向场解法 E波(TM) 1 2 1 2 2 2 2 2 2 1 1 2 2 2 2 2 2 2 2 2 2 1 1 ( ) 0 1 1 1 1 t z z z q z q z q z q E k E E E k e q E E k e q j E H k e q j E H k e q H波(TE) 1 2 1 2 2 2 2 2 2 1 1 2 2 2 2 2 2 2 2 2 2 1 1 ( ) 0 1 1 1 1 t z z z q z q z q z q H k H H H k e q H H k e q j H E k e q j H E k e q 直角坐标系 圆柱坐标系 拉梅系数

导波场论 回顾分离变量法一位函数法 0+9.团0=0 A为失量磁位,p为标量电位 V2A- A-w+r得 o-su or =0 0t2 洛伦茨规范又.A+c9=0 V2A-4 ∂2A =0 8r → 引入赫兹电矢量ZeA=ue OZe 8t n∂2ze V2Ze-ue ap =0 室分离n+1-0 p=-V.Z。 变量分离 0+(k2+y)p=0 E波只有i。=i(q,92)e
导 波 场 论 回顾 分离变量法——位函数法 2 ( ) 0 A t 2 2 2 ( ) A A A t t 2 2 2 2 2 2 0 0 t A A t Ze A t 引入赫兹电矢量Ze A 0 t 洛伦茨规范 2 2 2 0 e e e Z Z t Z 2 2 e e k 0 时空分离 1 2 ( , , ) j t Z q q z e e e 变量分离 1 2 ( , ) z e i q q e z E波只有 2 2 2 ( ) 0 t k A为矢量磁位, φ为标量电位

导波场论 回顾分离变量法一位函数法 利用赫兹电矢量求解E波(TM波)的电磁场 V+(k2+y2)p=0 边 中与E,就有相同的边界条件 界条件 求解中、Y或K。 E.=[k2+y2]eo- 由中求解出电磁场 E,=-N,p·eor- H,=josey,×(ie) 针对TEM波、H波(TE波)电磁场求解问题?
导 波 场 论 回顾 分离变量法——位函数法 2 2 2 ( ) 0 t k 利用赫兹电矢量求解E波(TM波)的电磁场 φ与Ez就有相同的边界条件 2 2 [ ] ( ) j t z z j t z t t j t z t t z E k e E e H j e i e 由φ求解出电磁场 求解φ、γ或Kc 边 界 条 件 针对TEM波、H波(TE波)电磁场求解问题?

导波场论 补充: 齐次亥姆赫兹方程 72E+k2E=0 7b+(k2+y2)p=0 V2H+k2五=0 不同坐标系下如何列方程? 如何求解方程和选择函数? 参考书:《数学物理方法》、《数理方程与特殊函数》 向同学们了解一下:A、学过;B、没有学过
导 波 场 论 补充: 齐次亥姆赫兹方程 2 2 2 2 0 0 k k E E H H 2 2 2 ( ) 0 t k 不同坐标系下如何列方程? 如何求解方程和选择函数? 参考书:《数学物理方法》、《数理方程与特殊函数》 向同学们了解一下:A、学过;B、没有学过

导波场论 >几种坐标的拉普拉斯算符 拉梅系数:位置点不变,不同坐标系描述曲线弧元长度 微量变化 ds=(dr)2+()'+(d)2 8 Oz 4】 + aq .dq ds,=H dq H= Ox dz 对其他维坐标同理有: Ox H,= i=1,2,3 aq, q;
导 波 场 论 几种坐标的拉普拉斯算符 拉梅系数:位置点不变,不同坐标系描述曲线弧元长度 微量变化 2 2 2 1 ds dx dy dz 222 1 111 x y z dq qqq 222 1 111 x y z H qqq 对其他维坐标同理有: 222 1,2,3 i iii x y z H i qqq 1 1 1 ds H dq
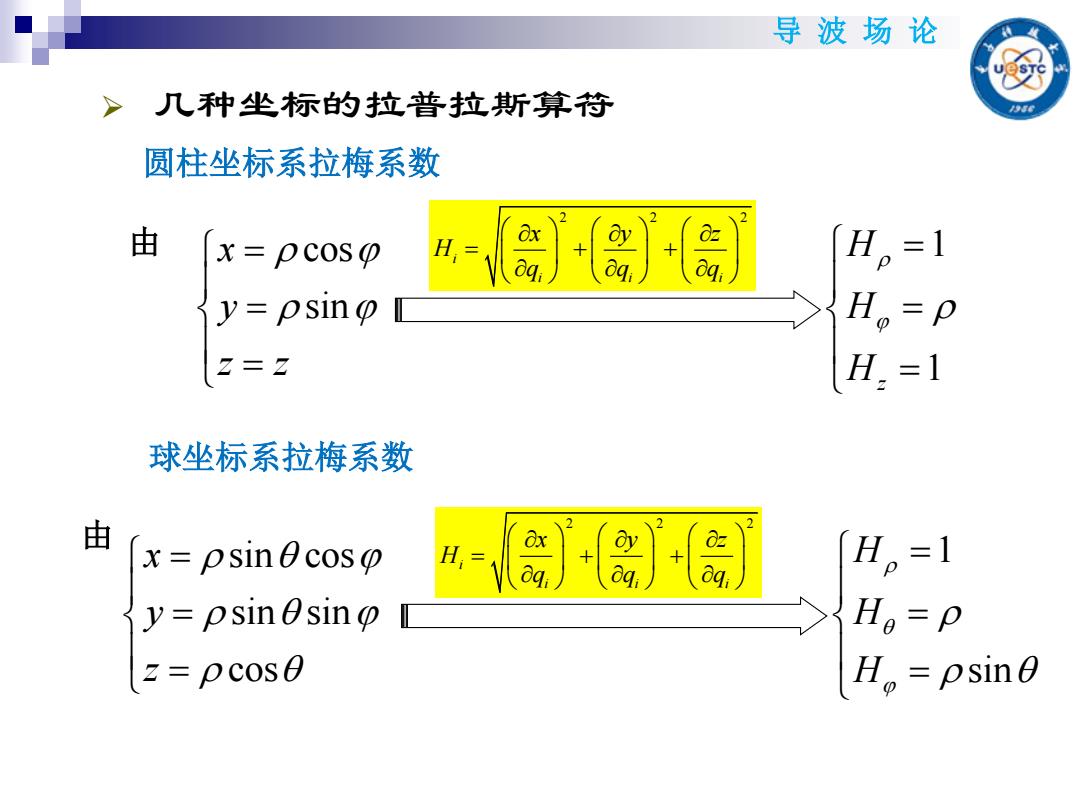
导波场论 几种坐标的拉普拉斯算符 圆柱坐标系拉梅系数 由 x=pcoso 8g, aq, H。=1 y=psino H。=P 2=z H.=1 球坐标系拉梅系数 由 x=psinθcosp H。=1 y=psinesino Ho=P z=pcos0 H。=osin0
导 波 场 论 几种坐标的拉普拉斯算符 圆柱坐标系拉梅系数 cos sin x y z z 由 1 1 z H H H 222 i iii x y z H qqq 球坐标系拉梅系数 sin cos sin sin cos x y z 由 1 sin H H H 222 i iii x y z H qqq

导波场论 > 几种坐标的拉普拉斯算符 梯度,某一函数在该点处的方向导数沿着该方向取得最大 值,梯度的长度是这个最大的变化率,标量函数u在坐标曲 线qi的切向单位矢量ei的投影变化率为: du 1 ou ds,H,oq; →>vw=2}e 台H,q 800 400 300 200 100 0 -20 Ax -15 -10 -5 T X+X△ 0 20 151050-5-10-15-20
导 波 场 论 几种坐标的拉普拉斯算符 梯度,某一函数在该点处的方向导数沿着该方向取得最大 值,梯度的长度是这个最大的变化率,标量函数u在坐标曲 线qi的切向单位矢量ei的投影变化率为: 1 i i i du u ds H q 3 1 1 i i i i u u e H q

导波场论 几种坐标的拉普拉斯算符 散度,表征空间各点矢量场发散的强弱程度,任意气块在 单位时间内其单位体积的变化率,矢量函数A在体积单元dV 向外流出的量 V.4=lim △V→0 △V 项,-品4M △q,△q3Aq: 91+△9192+△q293+△93 AV=」∫∫H,H,H,dq,dq-dq3=[H,H,1H]wAq,Aq△qs >7.A= HH,H aq ,(因片品4)
导 波 场 论 几种坐标的拉普拉斯算符 散度,表征空间各点矢量场发散的强弱程度,任意气块在 单位时间内其单位体积的变化率,矢量函数A在体积单元dV 向外流出的量 1 1 0 lim q n q S V A dS A V 1 1 2 2 3 3 1 2 3 1 3 3 3 2 3 1 3 3 1 2 3 q q q q q q M q q q V H H H dq dq dq H H H q q q 1 1 1 2 3 1 3 3 1 q n q S M A dS Ae H H q q q q 2 3 1 1 3 2 1 2 3 1 2 3 1 2 3 1 A H H A H H A H H A e e e + + H H H q q q