
回顾上次: 波导的激励(探针、环、孔) 了解谐振腔的学习内容 谐振腔的基本特性 模式函数 本次课程: 模式函数及正交性 谐振腔内电磁场的模式函数展开 谐振腔的自由振荡
回顾上次: 波导的激励(探针、环、孔) 了解谐振腔的学习内容 谐振腔的基本特性 模式函数 本次课程: 模式函数及正交性 谐振腔内电磁场的模式函数展开 谐振腔的自由振荡
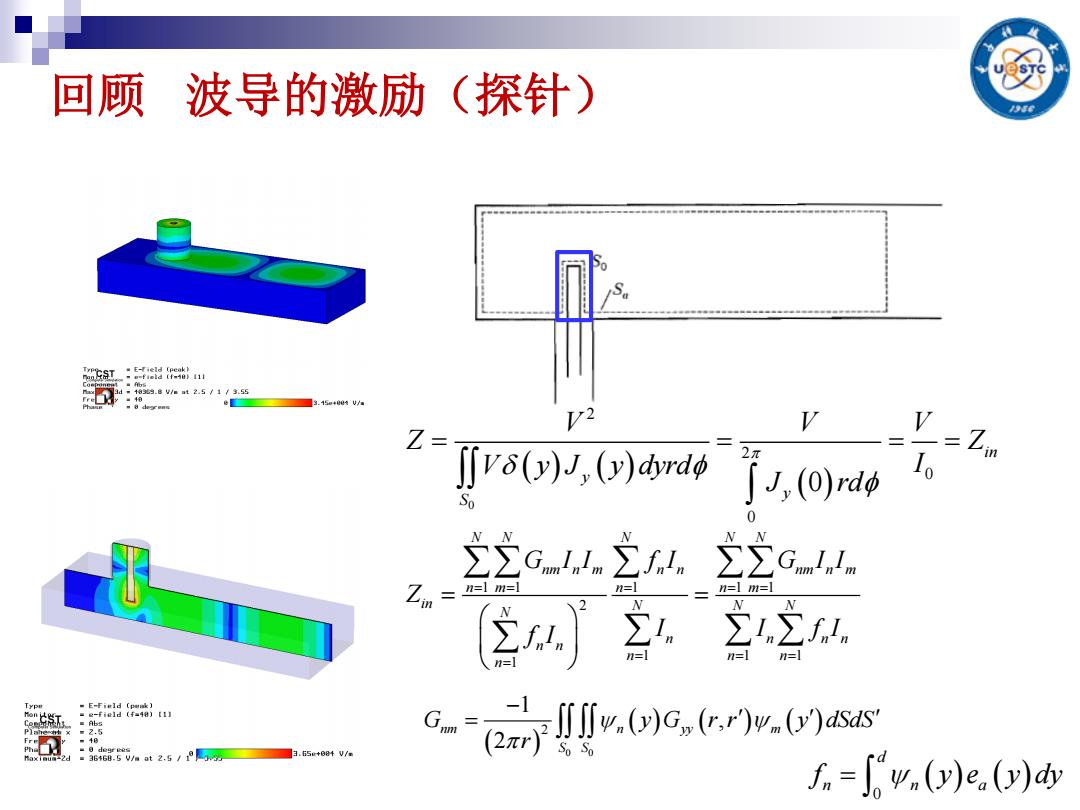
回顾 波导的激励(探针) d▣1839./at2.5/1/3.55 ☐3.15a44V/ V2 V Vδ(y)J,(y))rd J,ord 2π V=Zin Io So 1== ∑∑f1, n= n= mE-Fie1d〔pwk〕 ■e-fie1d(fa48)【1】 ■Abs ■2.5 Fr ▣48 0 degr ges 2 ·3668.5/aat2.5/3☐3.65+e4V/a c.aI.06,n.MS fn=∫04n(y)e(y)
回顾 波导的激励(探针) 0 2 2 0 0 0 in y y S V V V Z Z V y J y dyrd I J rd 1 1 1 1 1 2 1 1 1 1 N N N N N nm n m n n nm n m n m n n m in N N N N n n n n n n n n n n G I I f I G I I Z I I f I f I 0 0 2 1 , 2 nm n yy m S S G y G r r y dSdS r 0 d n n a f y e y dy
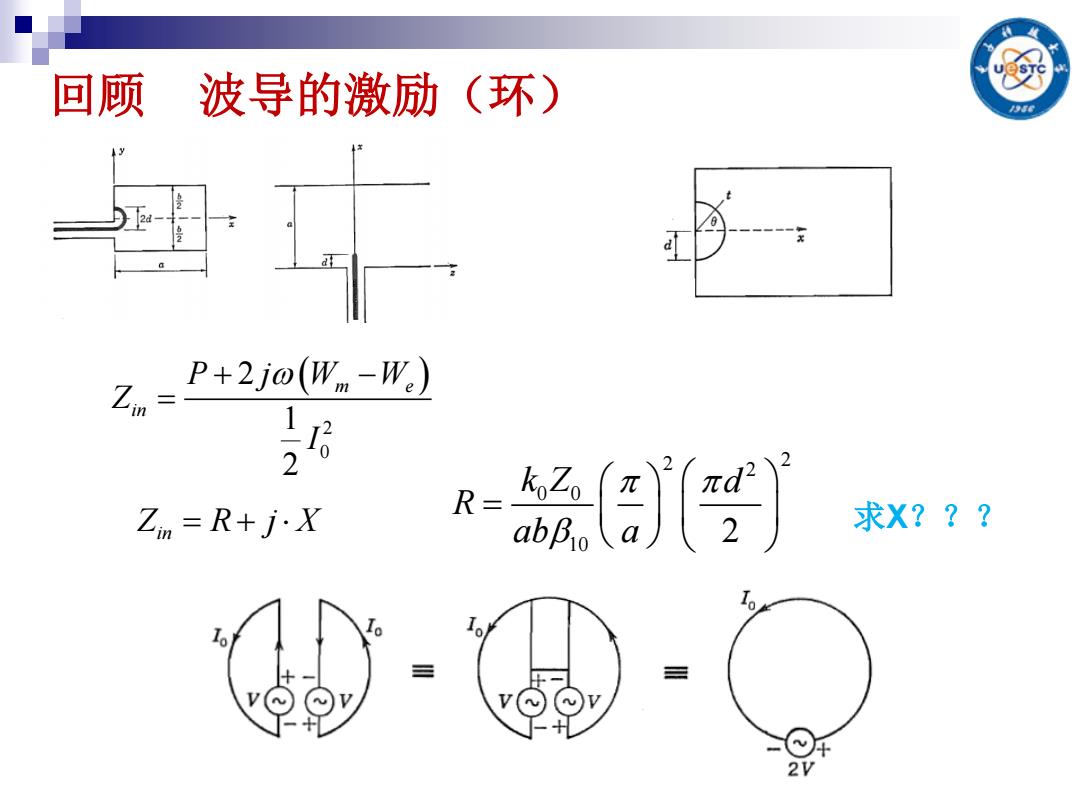
回顾波导的激励(环) P+2j0(Wm-W)) Zm=R+j·X R=- a川gj 求X??? 2V
回顾 波导的激励(环) Z R j X in 2 2 2 0 0 10 2 k Z d R ab a 2 0 2 1 2 m e in P j W W Z I 求X???

回顾2.12波导的激励(环) M=Iπd2 n-名足r0-r [x2+2+y-mb)] y=mb,m=0,±1,±2,. L-=×%K[%(e+4a门兴22[r+niar门 X=2na天线阵的势 Π2=Π,+Π2
回顾 2.12 波导的激励(环) 2 M I d 0 1/2 2 2 2 0 1 1/2 2 2 2 exp 4 m jk x z y mb M x z y mb y mb m , 0, 1, 2,... 1/2 1/2 ' 2 2 2 2 2 2 2 0 0 0 0 1 1 2 4 4 2 m n n m M M K jk z n a K z n a b b X=2na天线阵的势 z 1 2 +
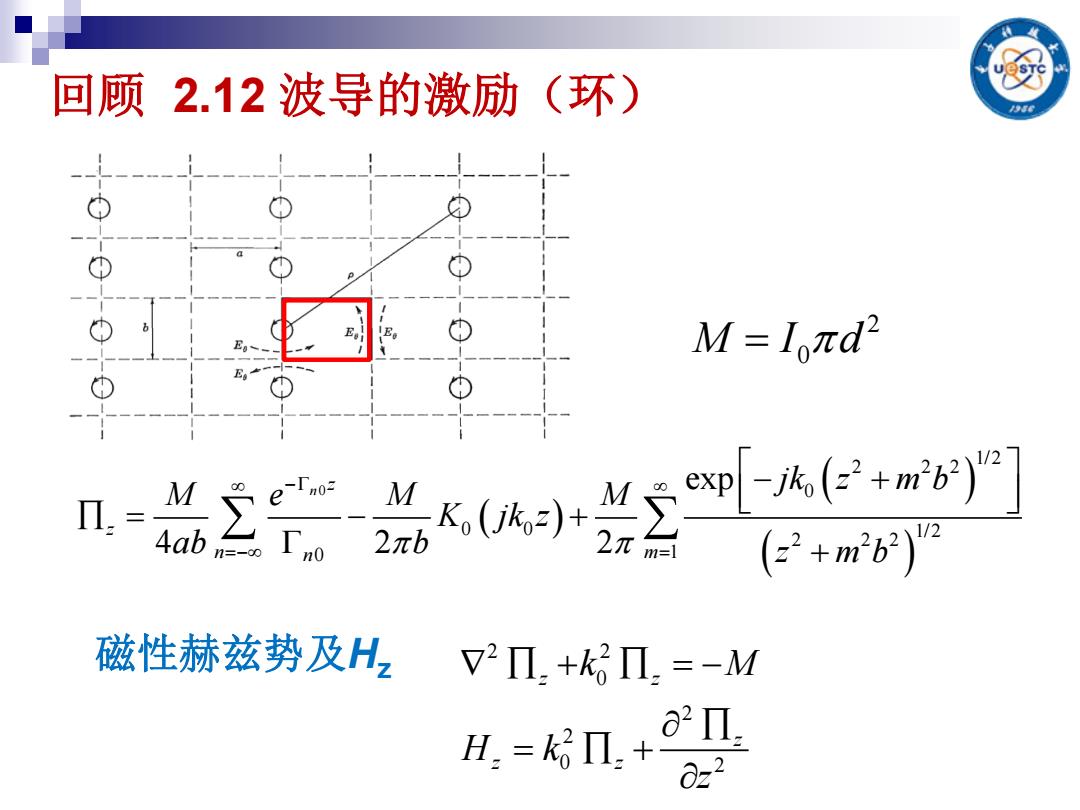
回顾2.12波导的激励(环) M=1πd2 n.= n=-0 xr 磁性赫兹势及H2 V2Π.+kΠ.=-M a2Π H=k6Π+ 0z2
回顾 2.12 波导的激励(环) 2 M I d 0 2 2 0 2 2 0 2 z z z z z k M H k z 磁性赫兹势及Hz 0 1/2 2 2 2 0 0 0 1/2 2 2 2 0 1 exp 4 2 2 n z z n m n jk z m b M e M M K jk z ab b z m b
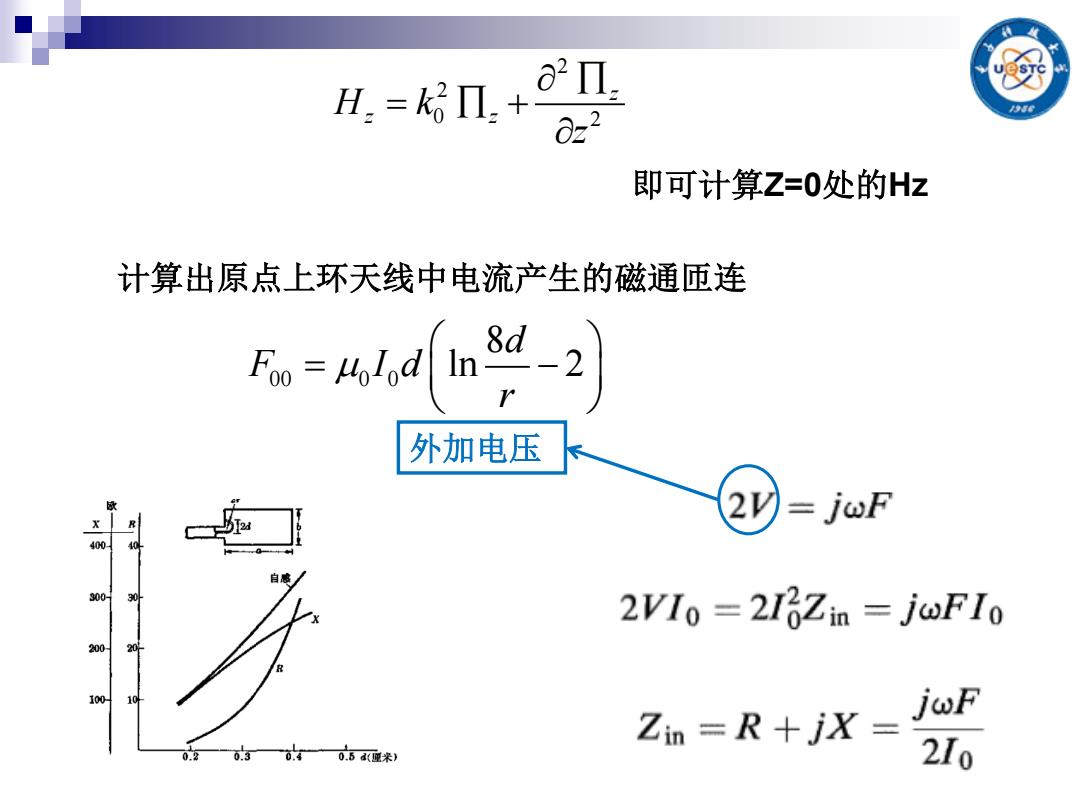
H:koI.+ 2Π: 0z2 即可计算Z=0处的Hz 计算出原点上环天线中电流产生的磁通匝连 8d 外加电压 2V=jwF 300- 30 2VIo=21Zin jwF Io 200 20 100 Zin =R+jX= joF 0.3 2I0
即可计算Z=0处的Hz 2 2 0 2 z H k z z z 计算出原点上环天线中电流产生的磁通匝连 00 0 0 8 ln 2 d F I d r 外加电压

回顾2.12波导的激励(孔) 等效电流定理 等效磁流定理 孔耦合在谐振腔后继续分析,深入讨论
回顾 2.12 波导的激励(孔) 等效电流定理 等效磁流定理 孔耦合在谐振腔后继续分析,深入讨论
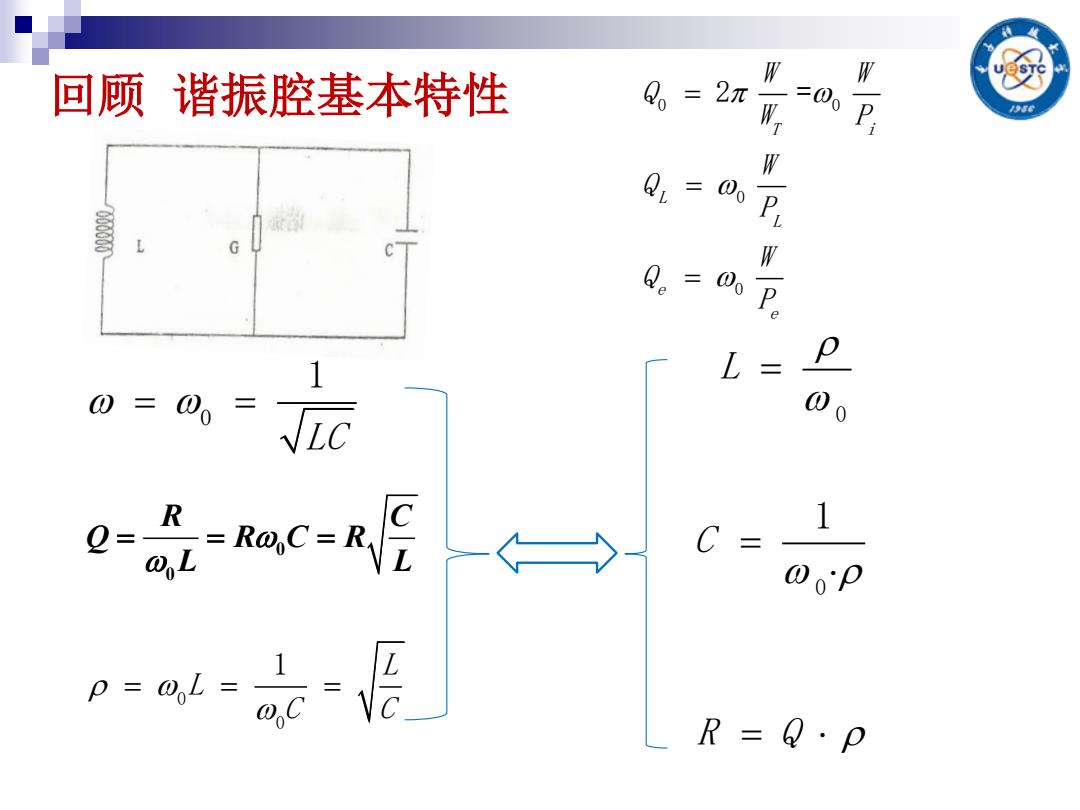
回顾谐振腔基本特性 W W 2 2π W 二00 W QL 00 160000 P L G W Q。 =00 P L 0= 00 0- R C p=a以=-店 R- Q·P
回顾 谐振腔基本特性 0 1 LC 0 0 R C Q R C R L L 0 0 1 L L C C 0 L 0 1 C R Q 0 0 0 0 2 = T i L L e e W W Q W P W Q P W Q P

回顾模式函数 定义:无散(有旋)模式Em和Hm为坐标的函数 满足:又×E。=k币。 V2E。+k2E=0 V×in=kE Vi。+k2且。=0 m=0、1、2... 在S上, E×n=0 在S上, E·五=O(i。⊥n) i。·方=0 电场强度分布 in×n=O(in∥) 磁场强度分布 无旋模式Fn和Gn定义为 中。 =0 a 2=0 on kF=V。 f。 ×五=0 。n 0 kG =VV 在S上, 0 在S上, w. :0 n=1,23... on G. n =0 Gn×五=0
回顾 模式函数 0、1、2... m m m m m m k k m E = H H E 2 2 2 2 m m m m m m k k E + E = 0 H + H = 0 在S上, 在S上, m m 0 E n = 0 H n = ( ) ( ) m m m m 0 E n = 0 H n H n = H n 定义:无散(有旋)模式 Em 和 Hm 为坐标的函数 无旋模式 Fn 和 Gn 定义为 1,2,3... n n n n n n k k n F G 在S上, 在S上, 0 0 0 n n n n n F n = 0 G n 0 0 0 n n n n n F n = G n 0 满足: 电场强度分布 磁场强度分布

(2)模式函数的正交性 ▣E、H的正交性 令E与H表示两个电场的无散模式函数,我们有: V·(En×V×E,)=V×En。V×E,-E·V×V×E V·(En×V×E)=V×E,●V×E-E,·V×V×E →V·(En×V×E,-En×V×E)=En又×V×EEn〈又×V×E, =0 V×V×E=k2EnV×V×E,=kE。 E,m和Hm为无散模式 V2E +k2E =0 →V·(E。×V×E-E。×V×E,)=(k-k恒。·E
(2)模式函数的正交性 E m m 、H 的正交性 令E m m 与H 表示两个电场的无散模式函数,我们有: ( )= m n m n m n E E E E E E ( - )= - m n n m n m m n E E E E E E E E 2 = m m m E E k 2 = n n n E E k ( 2 2 - )=( ) m n n m m n n m E E E E - E E k k Em 和 Hm为无散模式 2 A A A = - 2 2 m m m E + E = 0 k ( )= n m n m n m E E E E E E =0