
第三章传热 3.1传热的基本概念 3.2热传导 3.3对流传热 3.4辐射传热 3.5稳定传熟过程计算 3.6换热器 3.7几种特殊情况下的传热
3.1 传热的基本概念 第三章 传 热 3.2 热传导 3.3 对流传热 3.4 辐射传热 3.6 换热器 3.7 几种特殊情况下的传热 3.5 稳定传热过程计算

本章重点和难点 掌握导热、对流换热的基本规律及计算方法: 口熟悉各种热交换设备的结构和特点; 口掌握稳定综合传热过程的计算; ▣了解强化传热和热绝缘的措施
掌握导热、对流换热的基本规律及计算方法; 熟悉各种热交换设备的结构和特点; 掌握稳定综合传热过程的计算; 了解强化传热和热绝缘的措施。 本章重点和难点

传热在食品工程中的应用 食品加工过程中的温度沱制、灭菌过程以及 各种单元操作(如蒸馏、 蒸发、干燥、结晶等) 对温度有一定的要求。 可0站 本沙 传热:热量的传递:由于怎度差引起的能量转移 传热的推动力: 注意:热量自动的由高温区传向低温区
传热在食品工程中的应用 食品加工过程中的温度控制、灭菌过程以及 各种单元操作(如蒸馏、蒸发、干燥、结晶等) 对温度有一定的要求。 传热:热量的传递:由于温度差而引起的能量转移。 传热的推动力: 注意:热量自动的由高温区传向低温区

3.1传热的基本概念 3.1.1传热的基本方式 热的传递是由于系统内或物体内温度不同而引起的,根 据传热机理不同,传热的基本方式有三种: >热传导(conduction): >对流(convection); >辐射(radiation)
3.1.1 传热的基本方式 ➢热传导(conduction); 热的传递是由于系统内或物体内温度不同而引起的,根 据传热机理不同,传热的基本方式有三种: 3.1 传热的基本概念 ➢对流(convection); ➢辐射(radiation)

(1)热传导(又称导热)》 物体各部分之间不发生相对位移)仅信分子、原子和自 由电子等微观粒子的热运动而引起的热量传递称为热传导。 特点:没有物质的宏观位移 接知纳 ◆气体子做不规则热运动时相互碰撞的结果 ◆固体 导电体:怎由电子年晶格间的运动 非导电体:通过晶格的振动来实现的 ◆液体 机理复杂
物体各部分之间不发生相对位移,仅借分子、原子和自 由电子等微观粒子的热运动而引起的热量传递称为热传导。 特点:没有物质的宏观位移 (1)热传导(又称导热) 气体 分子做不规则热运动时相互碰撞的结果 固体 导电体:自由电子在晶格间的运动 非导电体:通过晶格结构的振动来实现的 液体 机理复杂

(2)热对流 流体部之间发生相对位移所引起的热传递过程称为热 对流。热对流仅发生在流孙中。 热对流的两种方式: >强制对流: 因泵(或风机)或搅拌等外力所导致的府流祢为强制对流 >自然对流: 由于流体各处的盒度不同而引起的密度差异,致使流体产 生相对位移,这种对流称为自然对沉 流动的原因不同,对流传热的规律也不同。在同一流体中 有可能同时发生自然对流和强制对流
➢强制对流: 因泵(或风机)或搅拌等外力所导致的对流称为强制对流。 流动的原因不同,对流传热的规律也不同。在同一流体中 有可能同时发生自然对流和强制对流。 热对流的两种方式: ➢自然对流: 由于流体各处的温度不同而引起的密度差异,致使流体产 生相对位移,这种对流称为自然对流。 (2)热对流 流体各部分之间发生相对位移所引起的热传递过程称为热 对流。 热对流仅发生在流体中

(3)热辐射 因热的原因而产生的电磁波在空间的传递, 称为热辐射。 所有物体都能将热以电磁波的形式发射出去, 而不需要任何 介质 >当辐射出来的电磁波遇到物体时, 被物体全部或者部分的吸 M 收而变为热能。一 >所以:辐射传热过程中不仅有热量的传递, 还伴随能量形式 的转化 任何物体只要在绝对零度以上都能发射辐射能,但是只有在 物体温度较高的时候, 垫辐射才能成为恶的代热形式, 实今上,上述三种传热方很少单独出现, 而往往是相互 伴随着出现的
(3)热辐射 因热的原因而产生的电磁波在空间的传递,称为热辐射。 ➢所有物体都能将热以电磁波的形式发射出去,而不需要任何 介质。 ➢当辐射出来的电磁波遇到物体时,被物体全部或者部分的吸 收而变为热能。 ➢所以:辐射传热过程中不仅有热量的传递,还伴随能量形式 的转化。 ➢任何物体只要在绝对零度以上都能发射辐射能,但是只有在 物体温度较高的时候,热辐射才能成为主要的传热形式。 实际上,上述三种传热方式很少单独出现,而往往是相互 伴随着出现的

3.1.2温度场和温度梯度 (1) 盒度场 温度场(temperature fielo):空间中各点在某一瞬间 的温度分布,称为温度场。 物体的温度分布是空间坐标和时间的函数,即 t=f(x,y,z, 式中:t一温度; xJ乃乙 空间坐标; 时间
➢ 温度场(temperature field):空间中各点在某一瞬间 的温度分布,称为温度场。 式中:t—— 温度; x, y, z —— 空间坐标; τ—— 时间。 物体的温度分布是空间坐标和时间的函数,即 t = f (x,y,z,τ) 3.1.2 温度场和温度梯度 (1)温度场
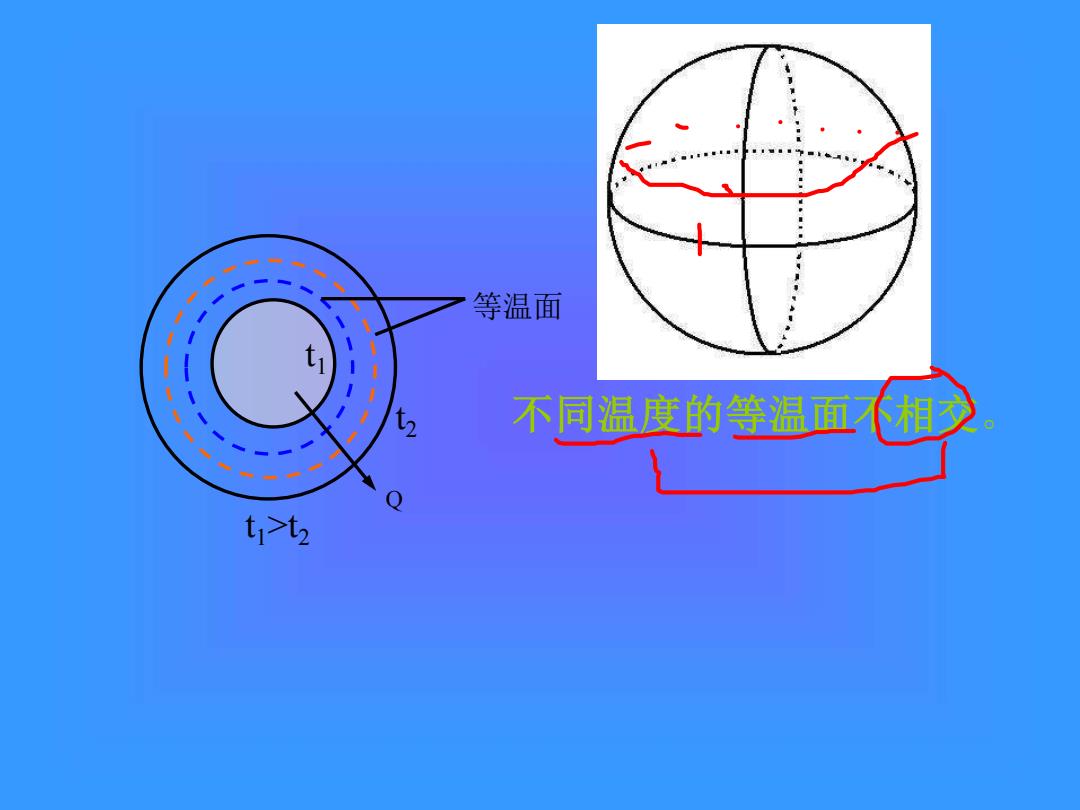
等温面 不同温度的等温面不相少 t1>t2
不同温度的等温面不相交。 t1 t2 t1>t2 等温面 Q

维温度场:若温度场中温度只沿着一个坐标方向变化。 一维温度场的温度分布表达式为: t=f(x,t) (4-1a) >不稳定温度场:温度场内如果各点温度随时间而改变。 >稳定温度场:若温度不随时间而改变。 >等温面:温度场中同一时刻相同温度各点组成的面。 等温面的特点: (1)等温面不能相交 (2)沿等温面无热量传递
一维温度场:若温度场中温度只沿着一个坐标方向变化。 一维温度场的温度分布表达式为: t = f (x,τ) (4-1a) 等温面的特点: (1)等温面不能相交; (2)沿等温面无热量传递。 ➢不稳定温度场:温度场内如果各点温度随时间而改变。 ➢稳定温度场:若温度不随时间而改变。 ➢等温面:温度场中同一时刻相同温度各点组成的面