山西能源学院教案 授课班级能动1701-1704 授课时间 计2学时 课题(章节 第四章热传导问题的数值解法 4.1导热问题数值求解的基本思想 及内容) 4.2内节点离散方程的建立方法 掌握导热问题数值解法的基本思路: 教学目的 利用热平衡法建立内节点的离散方程: 和要求 了解分析解法与数值解法的异同点。 重点 难点 内节点方程的建立方法 教学进程 (含课堂 教学内容:导热问题数值求解的基本步骤:热平衡法建立内节点 教学内容、 离散方程。 教学方法、 教学方法:讲授与练习、启发讨论、诱导式、归纳总结法。 辅助手段等) 作业布置 复习题1,2 主要 《传热学》第四版,杨世铭,陶文铨, 参考资料 高等教育出版社,2006年8月 课后自我 此章重点为热平衡法计算离散方程,傅里叶定律和三种边界条件 总结分析 是基础,要教会学生灵活运用,不能生搬硬套,否则在公式参数 的选取上将出现错误
山西能源学院教案 授课班级 能动 1701-1704 授课时间 计 2 学时 课题(章节 及内容) 第四章 热传导问题的数值解法 4.1 导热问题数值求解的基本思想 4.2 内节点离散方程的建立方法 教学目的 和要求 掌握导热问题数值解法的基本思路; 利用热平衡法建立内节点的离散方程; 了解分析解法与数值解法的异同点。 重 点 难 点 内节点方程的建立方法 教学进程 (含课堂 教学内容、 教学方法、 辅助手段等) 教学内容:导热问题数值求解的基本步骤;热平衡法建立内节点 离散方程。 教学方法:讲授与练习、启发讨论、诱导式、归纳总结法。 作业布置 复习题 1,2 主 要 参考资料 《传热学》第四版,杨世铭,陶文铨, 高等教育出版社,2006 年 8 月 课后自我 总结分析 此章重点为热平衡法计算离散方程,傅里叶定律和三种边界条件 是基础,要教会学生灵活运用,不能生搬硬套,否则在公式参数 的选取上将出现错误

山西能源学院教案 第四章热传导问题的数值解法 4-1导热问题数值求解的基本思想及内节点方程的建立 由前可知,求解导热问题实际上就是对导热微分方程在定解条件下的积分求 解,从而获得分析解。但是,对于工程中几何形状及定解条件比较复杂的导热问 题,从数学上目前无法得出其分析解。随着计算机技术的迅速发展,对物理问题 进行离散求解的数值方法发展得十分迅速,并得到广泛应用,并形成为传热学的 一个分支一计算传热学(数值传热学),这些数值解法主要有以下几种: (1)有限差分法(2)有限元方法(3)边界元方法 数值解法能解决的问题原则上是一切导热问题,特别是分析解方法无法解决 的问题。如:几何形状、边界条件复杂、物性不均、多维导热问题。 一.分析解法与数值解法的异同点: ·相同点:根本目的是相同的,即确定①=f(x,y,z);②g(x,y,z,) ·不同点:数值解法求解的是区域或时间空间坐标系中离散点的温度分布代替连 续的温度场:分析解法求解的是连续的温度场的分布特征,而不是分散点的数值。 二.解法的基本概念 ·实质 对物理问题进行数值解法的基本思路可以概括为:把原来在时间、空间坐标 系中连续的物理量的场,如导热物体的温度场等,用有限个离散点上的值的集合 来代替,通过求解按一定方法建立起来的关于这些值的代数方程,来获得离散点 上被求物理量的值。该方法称为数值解法。 这些离散点上被求物理量值的集合称为该物理量的数值解。 2、基本思路:数值解法的求解过程可用框图4-1表示。 由此可见: 1)物理模型简化成数学模型是基础:
山西能源学院教案 第四章 热传导问题的数值解法 4-1 导热问题数值求解的基本思想及内节点方程的建立 由前可知,求解导热问题实际上就是对导热微分方程在定解条件下的积分求 解,从而获得分析解。但是,对于工程中几何形状及定解条件比较复杂的导热问 题,从数学上目前无法得出其分析解。随着计算机技术的迅速发展,对物理问题 进行离散求解的数值方法发展得十分迅速,并得到广泛应用,并形成为传热学的 一个分支——计算传热学(数值传热学),这些数值解法主要有以下几种: (1)有限差分法 ( 2 )有限元方法 ( 3 )边界元方法 数值解法能解决的问题原则上是一切导热问题,特别是分析解方法无法解决 的问题。如:几何形状、边界条件复杂、物性不均、多维导热问题。 一.分析解法与数值解法的异同点: • 相同点:根本目的是相同的,即确定 ① t=f (x,y,z) ;② 。 • 不同点:数值解法求解的是区域或时间空间坐标系中离散点的温度分布代替连 续的温度场;分析解法求解的是连续的温度场的分布特征,而不是分散点的数值。 二.解法的基本概念 • 实质 对物理问题进行数值解法的基本思路可以概括为:把原来在时间、空间坐标 系中连续的物理量的场,如导热物体的温度场等,用有限个离散点上的值的集合 来代替,通过求解按一定方法建立起来的关于这些值的代数方程,来获得离散点 上被求物理量的值。该方法称为数值解法。 这些离散点上被求物理量值的集合称为该物理量的数值解。 2 、基本思路:数值解法的求解过程可用框图 4-1 表示。 由此可见: 1 )物理模型简化成数学模型是基础;
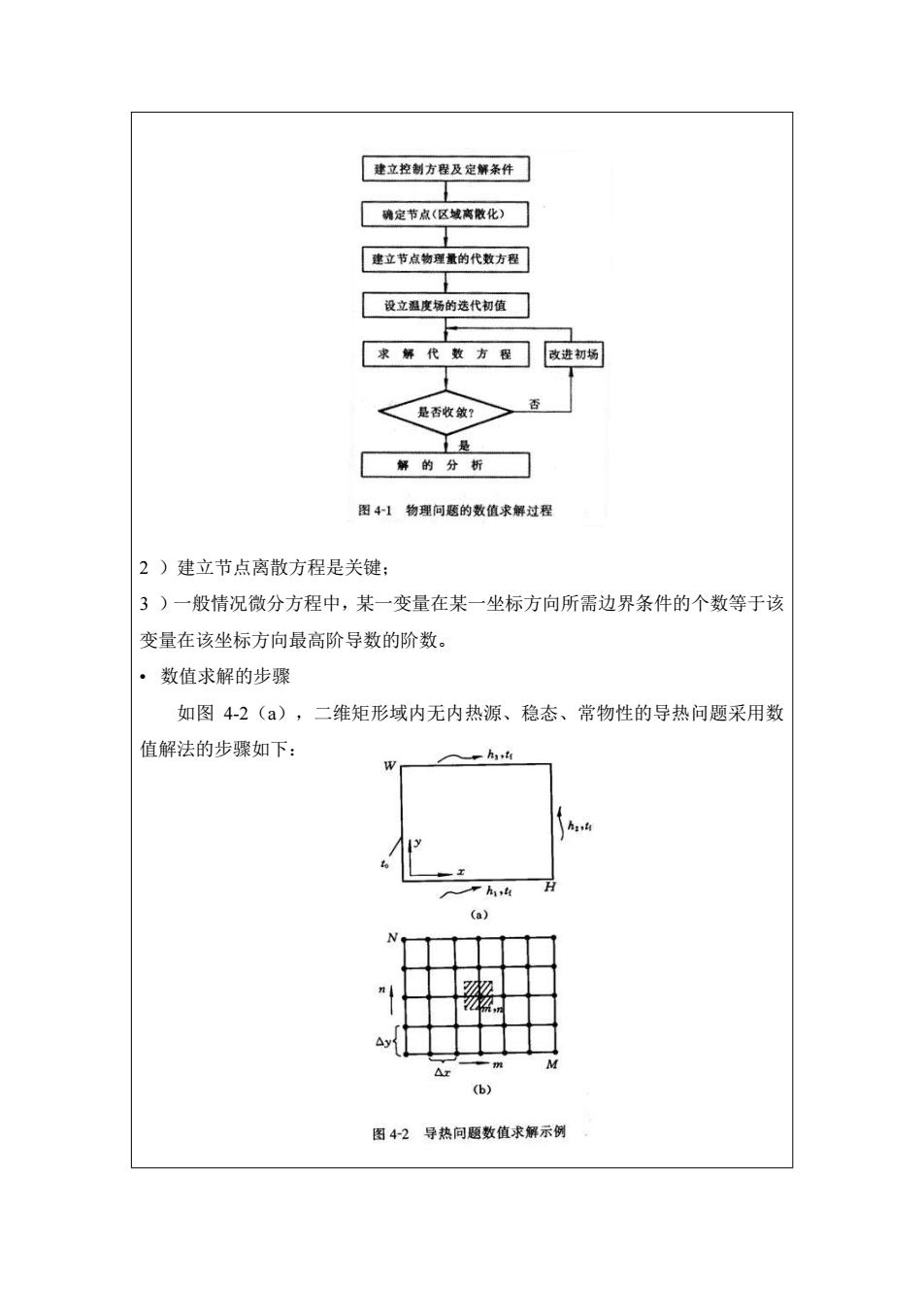
建立控制方程及定解条件 确定节点(区域离散化) 建立节点物理量的代数方程 设立温度场的选代初值 求解代数方程 改进初场 是否收敛? 是 解的分析 图41 物理问题的数值求解过程 2)建立节点离散方程是关键: 3)一般情况微分方程中,某一变量在某一坐标方向所需边界条件的个数等于该 变量在该坐标方向最高阶导数的阶数。 ·数值求解的步骤 如图4-2(a),二维矩形域内无内热源、稳态、常物性的导热问题采用数 值解法的步骤如下: h:4 Ph1,4 (a) 为 x (b) 图42导热问题数值求解示例
2 )建立节点离散方程是关键; 3 )一般情况微分方程中,某一变量在某一坐标方向所需边界条件的个数等于该 变量在该坐标方向最高阶导数的阶数。 • 数值求解的步骤 如图 4-2(a),二维矩形域内无内热源、稳态、常物性的导热问题采用数 值解法的步骤如下:

(1)建立控制方程及定解条件 控制方程:是指描写物理问题的微分方程。 针对图示的导热问题,它的控制方程(即导热微分方程)为: 821 82t +0=0 (4-1) 边界条件: x=0时,t=toa X=H时,-2 lx=H=2[(H,)-2] 当y0时,- l-0=4(x,0-y】 当y=w时,-2必 y=w=[(x,-r] (4-2) (2)区域离散化(确立节点) 用一系列与坐标轴平行的网格线把求解区域划分成若干个子区域,用网格线 的交点作为需要确定温度值的空间位置,称为节点(结点),节点的位置用该 节点在两个方向上的标号m,n表示。 相邻两节点间的距离称步长。△x,△y每个节点都可以看成是以它为中心 的一个小区域的代表把节点代表的小区域称为元体(又叫控制容积),如图42 (b)。 (3)建立节点物理量的代数方程(离散方程) 节点上物理量的代数方程称离散方程。其过程如下: ·首先划分各节点的类型: ·其次,建立节点离散方程: ·最后,代数方程组的形成。 对节点(m,n)的代数方程,当△x=△y时,有: (4-3) (4)设立迭代初场 代数方程组的求解方法有直接解法与迭代解法,传热问题的有限差分法中主 要采用迭代法。采用迭代法求解时,需对被求的温度场预先设定一个解,这个解 称为初场,并在求解过程中不断改进
(1) 建立控制方程及定解条件 控制方程:是指描写物理问题的微分方程 。 针对图示的导热问题,它的控制方程(即导热微分方程)为: ( 4-1 ) 边界条件: x=0 时,t = t0。 x=H 时, 当 y=0 时, 当 y=W 时, ( 4-2 ) (2)区域离散化(确立节点) 用一系列与坐标轴平行的网格线把求解区域划分成若干个子区域,用网格线 的交点作为需要确定温度值的空间位置,称为节点 ( 结点 ) ,节点的位置用该 节点在两个方向上的标号 m ,n 表示。 相邻两节点间的距离称步长。 △x, △y 每个节点都可以看成是以它为中心 的一个小区域的代表把节点代表的小区域称为元体(又叫控制容积),如图 4-2 (b) 。 (3)建立节点物理量的代数方程(离散方程) 节点上物理量的代数方程称离散方程。其过程如下: • 首先划分各节点的类型; • 其次,建立节点离散方程; • 最后,代数方程组的形成。 对节点 (m,n) 的代数方程,当 △x=△y 时,有: ( ( 4-3 ) (4)设立迭代初场 代数方程组的求解方法有直接解法与迭代解法,传热问题的有限差分法中主 要采用迭代法。采用迭代法求解时,需对被求的温度场预先设定一个解,这个解 称为初场,并在求解过程中不断改进

(5)求解代数方程组 求解时遇到的问题:①线性:②非线性;③收敛性等。 如图4-2(b),除m=1的左边界上各节点的温度已知外,其余(M-1)N 个节点均需建立离散方程,共有(M-1)N个方程,则构成一个封闭的代数方程 组。 1)线性代数方程组:代数方程一经建立,其中各项系数在整个求解过程中不再 变化: 2)非线性代数方程组:代数方程一经建立,其中各项系数在整个求解过程中不 断更新。 3)是否收敛判断:是指用迭代法求解代数方程是否收敛,即本次迭代计算所得 之解与上一次迭代计算所得之解的偏差是否小于允许值。 关于变物性(物性为温度的函数)导热问题,建立的离散方程,四个邻点 温度的系数不是常数,而是温度的函数。在迭代计算时,这些系数应不断更新, 这是非线性问题。 (6)解的分析 通过求解代数方程,获得物体中的温度分布,根据温度场应进一步计算通过 的热流量,热应力及热变形等。因此,对于数值分析计算所得的温度场及其它物 理量应作详细分析,以获得定性或定量上的结论。 三、稳态导热中位于计算区域内部的节点离散方程的建立方法 1、基本概念 ·内节点:位于计算区域内部的节点,称内节点: ·差分格式:差商中的差分可以用向前、向后、 中心差分表示的格式。 2、基本方法 方法:①泰勒级数展开法(了解):②热 图43内节点离散方程的建立 平衡法(掌握)。 热平衡法: 其本质是傅里叶导热定律和能量守恒定律的体现。对每个元体,可用傅里叶 导热定律写出其能量守恒的表达式。如图4-3所示,元体在垂直纸面方向取单
(5)求解代数方程组 求解时遇到的问题: ① 线性; ② 非线性; ③ 收敛性等。 如图 4-2( b ),除 m=1 的左边界上各节点的温度已知外,其余 (M-1) N 个节点均需建立离散方程,共有 (M-1) N 个方程,则构成一个封闭的代数方程 组。 1 )线性代数方程组:代数方程一经建立,其中各项系数在整个求解过程中不再 变化; 2 )非线性代数方程组:代数方程一经建立,其中各项系数在整个求解过程中不 断更新。 3 )是否收敛判断:是指用迭代法求解代数方程是否收敛,即本次迭代计算所得 之解与上一次迭代计算所得之解的偏差是否小于允许值。 关于变物性 ( 物性为温度的函数 ) 导热问题,建立的离散方程,四个邻点 温度的系数不是常数,而是温度的函数。在迭代计算时,这些系数应不断更新, 这是非线性问题。 (6)解的分析 通过求解代数方程,获得物体中的温度分布,根据温度场应进一步计算通过 的热流量,热应力及热变形等。因此,对于数值分析计算所得的温度场及其它物 理量应作详细分析,以获得定性或定量上的结论。 三、稳态导热中位于计算区域内部的节点离散方程的建立方法 1 、基本概念 • 内节点:位于计算区域内部的节点,称内节点; • 差分格式:差商中的差分可以用向前、向后、 中心差分表示的格式。 2 、基本方法 方法:① 泰勒级数展开法(了解); ② 热 平衡法(掌握)。 热平衡法: 其本质是傅里叶导热定律和能量守恒定律的体现。对每个元体,可用傅里叶 导热定律写出其能量守恒的表达式。如图 4-3 所示,元体在垂直纸面方向取单

位长度,通过元体界面(w,e,n,s)所传导的热流量可以对有关的两个节点根据傅 里叶定律写出: 从节点(m-l,n)通过界面w传导到节点(m,n)的热流量: Φw=24yn-1,为-4m,n △x (4-4) 同理:通过界面e,n,s传导给节点(m,n)的热流量: Φe=4ym+ln-tm,n △x (4-5) 重n=2弘xm,n+1-m,n △y (4-6) 重。=2xm,n-1-m,n &)y (4-7) 对元体(m,n).根据能量守恒定律可知: 重w+④。十玉+④,=0 (4-8) 其中,规定:导入元体(m,n)的热流量为正:导出元体(m,n)的热流 量为负。 说明:①上述分析与推导是在笛卡儿坐标系中进行的: ②热平衡法概念清晰,过程简捷: ③热平衡法与$2一2建立微分方程的思路与过程一致,但不同的是前者是有 限大小的元体,后者是微元体
位长度,通过元体界面 (w,e,n,s) 所传导的热流量可以对有关的两个节点根据傅 里叶定律写出: 从节点 (m-1,n) 通过界面 w 传导到节点 (m,n) 的热流量: ( 4-4 ) 同理:通过界面 e,n,s 传导给节点( m,n )的热流量: ( 4-5 ) ( 4-6 ) ( 4-7 ) 对元体 (m,n). 根据能量守恒定律可知: ( 4-8 ) 其中,规定:导入元体( m,n )的热流量为正;导出元体( m,n )的热流 量为负。 说明:① 上述分析与推导是在笛卡儿坐标系中进行的; ② 热平衡法概念清晰,过程简捷; ③ 热平衡法与 §2 — 2 建立微分方程的思路与过程一致,但不同的是前者是有 限大小的元体,后者是微元体。 折叠