山西能源学院：《传热学》课程教学资源（PPT课件）第三章 非稳态热传导

第3章非稳态导热 主要内容态导热过程中温度场的变化规律及导热量 的分析求解方法。包括： 1.对流边界条件下一维瞬态导热的分析解法； 2.非稳态导热的集总参数分析法： 3.半无限大固体的非稳态导热； 4.周期性边界条件下的非稳态导热： 3.1非稳态导热的基本概念 t=f(x,y,z,t) 3.1.1非稳态导热问题的类型及特点 (1)瞬态导热 (2)周期性非稳态导热 2

2 第3 章 非稳态导热 3.1.1 非稳态导热问题的类型及特点 （1）瞬态导热 （2）周期性非稳态导热 3.1 非稳态导热的基本概念 非稳态导热过程中温度场的变化规律及导热量 的分析求解方法。包括： 1. 对流边界条件下一维瞬态导热的分析解法； 2. 非稳态导热的集总参数分析法； 3. 半无限大固体的非稳态导热 ； 4. 周期性边界条件下的非稳态导热； 主要内容： t = f (x, y, z, )

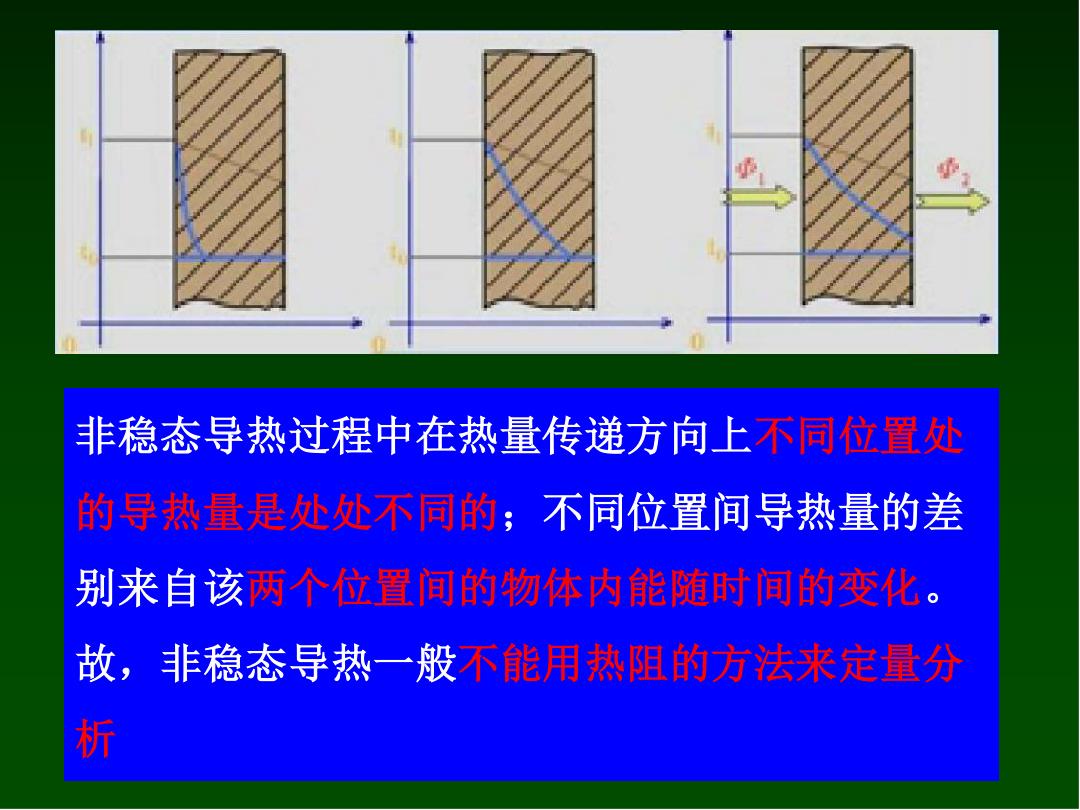
非稳态导热过程中在热量传递方向上不同位置处 的导热量是处处不同的；不同位置间导热量的差 别来自该两个位置间的物体内能随时间的变化 故，非稳态导热一般不能用热阻的方法来定量分 析

3 非稳态导热过程中在热量传递方向上不同位置处 的导热量是处处不同的；不同位置间导热量的差 别来自该两个位置间的物体内能随时间的变化。 故，非稳态导热一般不能用热阻的方法来定量分 析

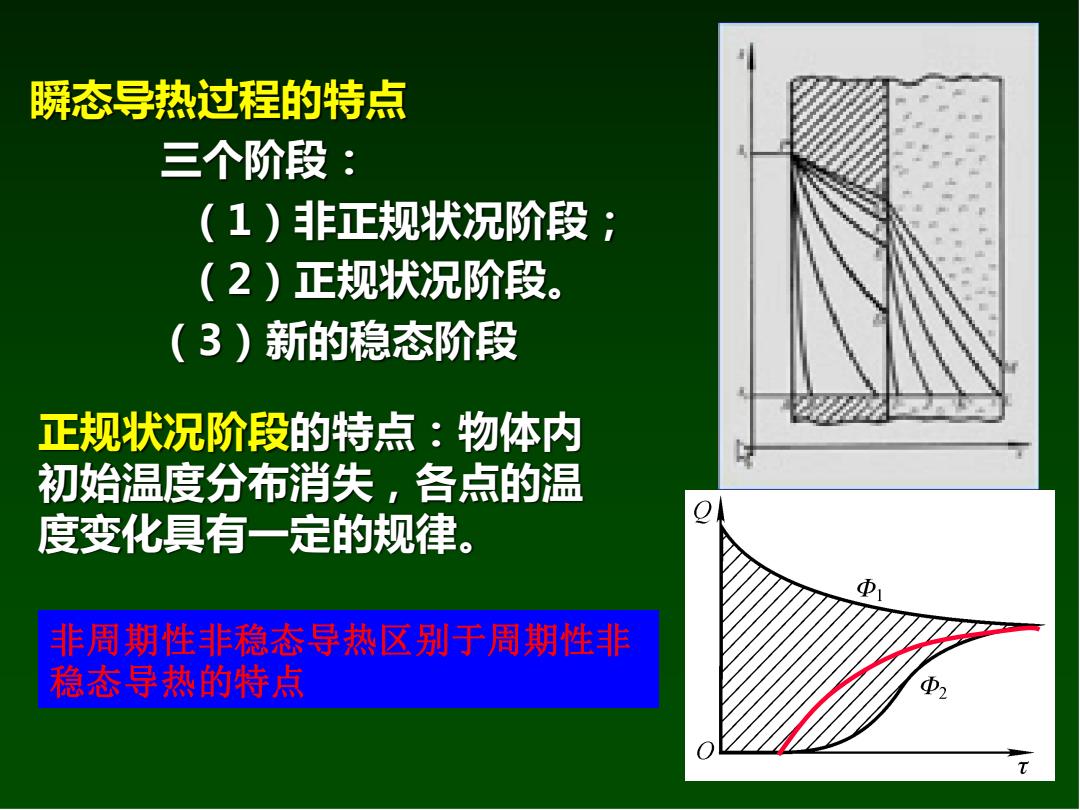
瞬态导热过程的特点 三个阶段 (1)非正规状况阶段： (2)正规状况阶段。 (3)新的稳态阶段 正规状况阶段的特点：物体内 初始温度分布消失，各点的温 度变化具有一定的规律。 非周期性非稳态导热区别于周期性非 稳态导热的特点

4 瞬态导热过程的特点 三个阶段： （1）非正规状况阶段； （2）正规状况阶段。 （3）新的稳态阶段 正规状况阶段的特点：物体内 初始温度分布消失，各点的温 度变化具有一定的规律。 非周期性非稳态导热区别于周期性非 稳态导热的特点

第三类边界条件下B数对平板中温度分布的影响 hδ (δ/2) 举例：平板冷却问题 Bi= (1/h) t=f(x,y,,0)=t 0 0 =0 x兰0 T=0 工 t2. 2 T2 T3 0 6 x 0 o' -0 0 (b)Bi→0 (a)Bio∞ ./h 5

5 ( ) (1 ) h Bi h     = = 第三类边界条件下Bi数对平板中温度分布的影响 举例：平板冷却问题 0 t = f (x, y,z,0) = t

3.2集总参数法（B≤0.1） 当B≤0.1时，物体内部的导热热阻远小于其表面的 对流换热热阻，可以忽略，物体内部各点的温度在任一 时刻都近似于均匀，物体的温度只是时间的函数。对于 这种情况，只须求解物体温度随时间的变化规律以及物 体放出或吸收的热量。一忽略无体内导热热阻的简化分 析方法成为集总参数法 假设：一个任意形状的物体，体 积为V,表面面积为A,密度p、比热 容c及热导率为常数，无内热源，初 始温度为。突然将该物体放入温度 恒定的流体中，物体表面和流体之 间对流换热的表面传热系数h为常数 假设该问题满足B≤0.1的条件

6 3.2 集总参数法（ Bi0.1） 当Bi0.1时，物体内部的导热热阻远小于其表面的 对流换热热阻，可以忽略，物体内部各点的温度在任一 时刻都近似于均匀，物体的温度只是时间的函数。对于 这种情况，只须求解物体温度随时间的变化规律以及物 体放出或吸收的热量。-忽略无体内导热热阻的简化分 析方法成为集总参数法 假设：一个任意形状的物体，体 积为V，表面面积为A，密度、比热 容c及热导率为常数，无内热源，初 始温度为t0。突然将该物体放入温度 t f恒定的流体中，物体表面和流体之 间对流换热的表面传热系数h为常数。 假设该问题满足Bi0.1的条件

根据能量守恒，单位时间物体热力学能的变化量应 该等于物体表面与流体之间的对流换热量 =-hA(t-t) o=1 =-hA0 hA dr hA x=0,0=0=t0-t hA In- I=VIA hA h(A)元 T hlλx hl ar 22 =Bi,·FO BMFo=exp(-Bi,·Fo) 下角标V表示以 I=V/A为特征长度

7 根据能量守恒，单位时间物体热力学能的变化量应 该等于物体表面与流体之间的对流换热量， ( f ) dt cV hA t t d   = − − f  = −t t d cV hA d     = − d hA d cV     = −0 , 0 0 f    = = = − t t 0 0 d hA d cV        = −   0 ln hA cV     = − 0 exp hA cV hA e cV       −   = = −    ( ) ( ) 2 hA h V A cV c V A      =  2 h l c l     =  2 V V hl a Bi Fo l   =  =  ( ) 0 exp Bi Fo V V V V e Bi Fo   −  = = −  下角标V 表示以 l=V/A为特征长度 l=V/A

在0~x时间内物体和周围环境之间交换的热量 2:pcV(to-t)=pcV(0-0) prapre(-e 令Q,=pcV表示物体温度从t,变化到周围流体温度1 所放出或吸收的总热量，则上式改写为 =1-e-Biv-For 上述分析结果既适用于物体被加热的情况，也适用 于物体被冷却的情况。 8

8 在0~ 时间内物体和周围环境之间交换的热量 Q cV t t  = −  ( 0 )= −    cV ( 0 ) 0 0 cV 1       = −     0 (1 ) Bi Fo V V   cV e−  = − 令 Q cV 0 0 =   ，表示物体温度从t0 变化到周围流体温度t f 所放出或吸收的总热量，则上式改写为 0 1 Q Bi Fo V V e Q  −  = − 上述分析结果既适用于物体被加热的情况，也适用 于物体被冷却的情况

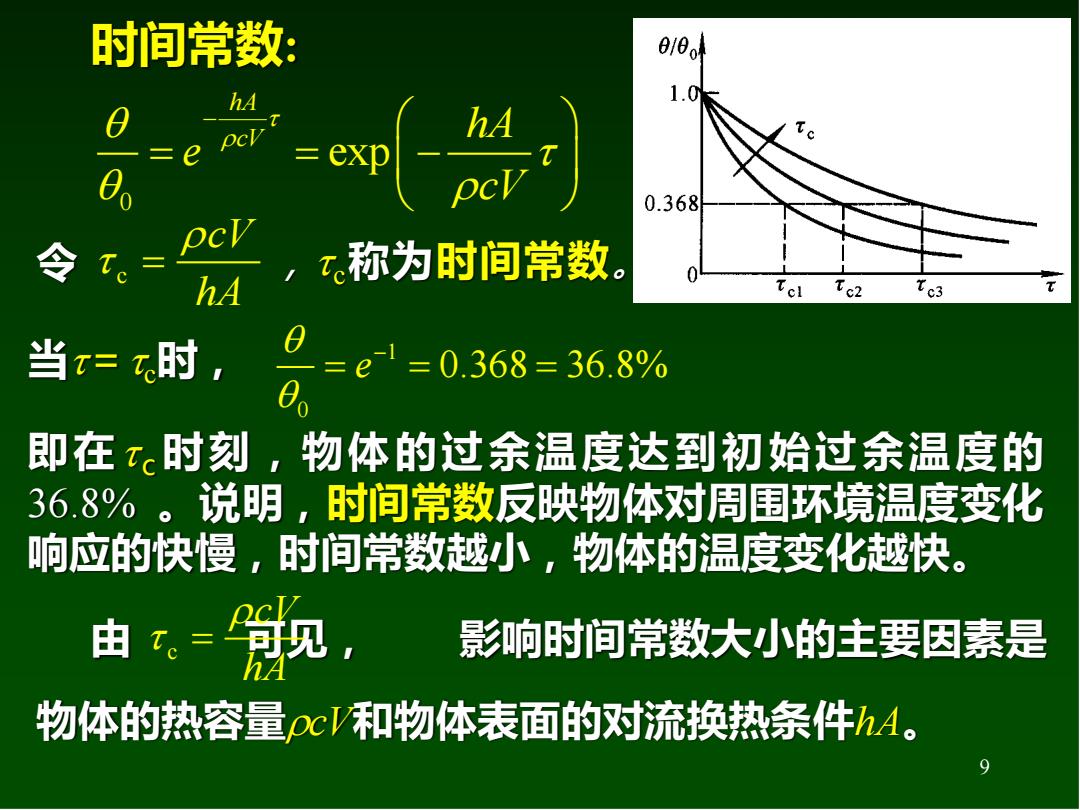
时间常数： 1.0 hA T 0.368 令 To= ,称为时间常数。 hA Tc2 Tc3 当x=时， 日=e=0.368=36.8% 即在x时刻，物体的过余温度达到初始过余温度的 36.8%。说明，时间常数反映物体对周围环境温度变化 响应的快慢，时间常数越小，物体的温度变化越快。 由飘， 影响时间常数大小的主要因素是 物体的热容量ρc和物体表面的对流换热条件hA

9 令 c cV hA   = ， c称为时间常数。 0 exp hA cV hA e cV       −   = = −    当＝c时， 1 0 e 0.368 36.8%   − = = = 即在 c时刻，物体的过余温度达到初始过余温度的 36.8% 。说明，时间常数反映物体对周围环境温度变化 响应的快慢，时间常数越小，物体的温度变化越快。 由 c 可见， 影响时间常数大小的主要因素是 cV hA   = 物体的热容量cV和物体表面的对流换热条件hA。 时间常数:

几点说明： (1)集总参数法中的毕渥数B,与傅里叶数Fo以 1=VA为特征长度 h(VA)<0.IM λ 对厚为2δ的 N M=1 Aδ 无限大平板 δ Biy =B A A M= V πRp R 对半径为R的 B 2 A 2nRp 2 2 无限长圆柱 4 πR 对半径为R的 M= 3 R B 3 球 A 4πR 3 3 (2)对于形状如平板、柱体或球的物体，只要满足 B≤0.1，就可以使用集总参数法计算，偏差小于5%。 0

10 几点说明： （1）集总参数法中的毕渥数BiV与傅里叶数FoV以 l=V/A为特征长度 （2）对于形状如平板、柱体或球的物体，只要满足 Bi0.1，就可以使用集总参数法计算，偏差小于5％。 3 1 M 2 1 M M 1 = = = 3 B B 3 R 4 R R 3 4 A V 2 B B 2 R 2 R R A V B B A A A V i 2 i v 3 i i v 2 i v i = = = = = = = = =        对厚为2δ的  无限大平板 对半径为R的 无限长圆柱 对半径为R的 球 0.1M h(V A) Bi v =  

例题：用不锈钢做底板的家用电熨斗初始时处于室温，。当 接通开关后电热器在底板内以 9W/m3 的强度发热。不锈钢 的热物性参数均已知，不锈钢底板的体积为 V,暴露于空 气中的表面积为A,该表面与空气间的表面传热系数为， 忽略不锈钢底板的内热阻 1)不考虑热辐射的影响，试用集总参数法分析电熨斗底板 的温度变化规律 2)若考虑电熨斗底板与房间的辐射换热，电熨斗底板的发 射率为ε，写出该非稳态导热的完整数学描述

11 例题：用不锈钢做底板的家用电熨斗初始时处于室温 。当 接通开关后电热器在底板内以 的强度发热。不锈钢 的热物性参数均已知，不锈钢底板的体积为 ，暴露于空 气中的表面积为 ，该表面与空气间的表面传热系数为 ， 忽略不锈钢底板的内热阻 1）不考虑热辐射的影响，试用集总参数法分析电熨斗底板 的温度变化规律 2）若考虑电熨斗底板与房间的辐射换热，电熨斗底板的发 射率为ε，写出该非稳态导热的完整数学描述 f t f t f t 3 qv W m V A h