
工程热力学第5版题解 第四章气体和蒸汽的热力过程 4-1有2.3kg的C0,初态T=477K,P,=0.32MPa,经可逆定容加热,达终温 T,=600K,设C0为理想气体,求△U、△H、△S,过程功及过程热量。(1)比热容为定 值:(2)比热容为变值,按气体性质表计算。 提示和答案:无论比热容是否定值,理想气体热力学能和焓只是温度的函数,定容过程 功为零。定值比热容:△U=209.94k、△H=293.92kJ、△S=0.3916kJ/K、W=0、 Q=△U=209.94kJ:变比热容:△U=219.10×103J、△H=303.08×103J、W=0、 △S=0.4186kJ/K、Q=△U=219.10kJ. 4-2甲烷CH,的初始状态2=0.47MPa,T=393K,经可逆定压冷却对外放出热量 4110.76J/mol,试确定其终温及1 molCH4的热力学能变化量△U。、焓变化量△H。。设甲 烷的比热容近似为定值,c。=2.3298kJ/kg·K)。 提示和答案:压力不高,甲烷处于理想气体状态,热力学能和焓只是温度的函数。 T,=283K、△Um=-3196.11J/mol、△Hn=-4110.76J/mol。 4-3氧气由1=40℃,B,=0.1MPa被压缩到P2=0.4MPa,试计算压缩1kg氧气消耗 的技术功。(1)按定温压缩计算:(2)按绝热压缩计算,设比热容为定值:(3)将它们表示 p-v图和T-s图上,试比较两种情况技术功大小。 提示和答案:理想气体定温压缩技术功等于膨胀功,绝热压缩技术功等于焓差 "x=-112.82J/kg、w=-138.34kg;在 Pⅴ图上定温压缩和绝热压缩技术功分别以图 4-1面积1-2,-m-n-1和1-2.-m-n-1表 示,x<W。,在T-s图上,定温过程 r=9r,用面积1-2,-m-n-1表示,绝热 图4-1 过程w=h-h=h,-h。,用面积1-2,-27-m-n-1表示,显见Wx<"。 4-4同上题,若比热容为变值,试按气体热力性质表计算绝热压缩1kg氧气消耗的技 术功。 20
工程热力学第 5 版题解 20 图 4-1 第四章 气体和蒸汽的热力过程 4-1 有 2.3kg 的 CO,初态 1 1 T p 477K 0.32MPa , ,经可逆定容加热,达终温 2 T 600K ,设 CO 为理想气体,求 U 、H 、S ,过程功及过程热量。(1)比热容为定 值;(2)比热容为变值,按气体性质表计算。 提示和答案:无论比热容是否定值,理想气体热力学能和焓只是温度的函数,定容过程 功为零。 定值比热容: U 209.94kJ 、 ΔH 293.92kJ 、 S 0.3916kJ/K 、W 0 、 Q U 209.94kJ ;变比热容: 3 U 219.10 10 J 、 3 H 303.08 10 J 、 W 0 、 S 0.4186kJ/K 、Q U 219.10kJ 。 4-2 甲烷 CH4 的初始状态 1 1 p T 0.47MPa 393K , ,经可逆定压冷却对外放出热量 4 110.76 J/mol ,试确定其终温及 4 1molCH 的热力学能变化量 U m 、焓变化量 H m 。设甲 烷的比热容近似为定值, 2.329 8kJ/(kg K) p c 。 提示和答案: 压力不高,甲烷处于理想气体状态,热力学能和焓只是温度的函数。 2 T 283K 、 m U 3196.11J/mol 、 m H 4110.76J/mol。 4-3 氧气由 1 1 t p 40 C 0.1MPa , 被压缩到 2 p 0.4MPa ,试计算压缩 1kg 氧气消耗 的技术功。(1)按定温压缩计算;(2)按绝热压缩计算,设比热容为定值;(3)将它们表示 p v 图和 T s 图上,试比较两种情况技术功大小。 提示和答案: 理想气体定温压缩技术功等于膨胀功,绝热压缩技术功等于焓差 t, 112.82J/kg w T 、 t , 138.34kJ/kg w s ;在 p-v 图上定温压缩和绝热压缩技术功分别以图 4-1 面积 1 2 1 T m n 和 1 2 1 s m n 表 示 , w w t, t, T s ,在 T-s 图 上,定 温过程 w q t,T T ,用面积 1 2 1 T m n 表示,绝热 过程 w h h h h t, 1 2 2 2 s T s ,用面积 1 2 2 1 s T m n 表示,显见 w w t, t, T s 。 4-4 同上题,若比热容为变值,试按气体热力性质表计算绝热压缩 1 kg 氧气消耗的技 术功

工程热力学第5版题解 提示和答案: 由附表8插值求出T=313K时,H。,和S0。因定熵过程 △S=S8,-S-RInB=0,所以S=S+Rn=21797Jmol.K。由同表据 S02得T=460.08K,H2=13546.39J/mol,= MH-Ha)=-13821x10Jkg。 453kg空气从P,=1MPa、T=900K,绝热膨胀到p,=0.1MPa。设比热容为定值, 绝热指数K=1.4,求:(1)终态参数T,和V,:(2)过程功和技术功:(3)△U和△H。 提示和答案:绝热过程过程功和技术功分别等于热力学能减少量和焓减少量。 T=466.17K、y,=1.3379m3/kg、W=934.47kJ、W=1308.26kJ、△U=-934.47kJ、 △H=-1308.26kJ。 4-6同上题,比热容为变值,按空气热力性质表重新进行计算。 提示和答案:利用P,=BP,查附表7得I,进而查得,不论比热容是否取定值, p 绝热过程过程功和技术功分别等于热力学能减少量和焓减少量。W=983.22k、 W=1336.82kJ。 4-71kg空气初态为P=0.5MPa,T=1000K,按定熵过程:(1)变化到工,=500K, 试确定P,:(2)变化到p,=0.1MPa确定T,。空气的c,可由空气真实热容公式确定: ==363-1337×10{T+3294×10*{T只-1913×10{7T+02763×10{ R 将计算结果与利用气体性质表求出的值进行比较。 业00=a,瑞'0=石4u-=sV○#(D紫绿 P 在C。na二-Rn上=0,用迭代法得出工=657.4K。(a)根据1 (2) P 查得P,=115.97P2=8.5555,所以P,=2A=0.03689MPa:(b)已知P,TP,得 P P2=23.194根据P2,查得T=657.419K,表明用真实比热容式积分所得的结果与气体性 质表得出的结果是一致的,但后一方法更方便。 21
工程热力学第 5 版题解 21 提示和答案: 由附表 8 插值求出 1 T 313K 时, Hm,1 和 0 m,1 S 。因定熵过程 0 0 2 m,2 m,1 1 ln 0 p S S S R p ,所以 0 0 2 ,2 ,1 1 ln 217.97J/(mol K) m m p S S R p 。由同表据 0 m,2 S 得 2 T 460.08K , m,2 H 13546.39J/mol , 3 t, m,1 m,2 1 ( ) 138.21 10 J/kg w H H s M 。 4-5 3 kg 空气从 1 p 1MPa 、 1 T 900K ,绝热膨胀到 2 p 0.1MPa 。设比热容为定值, 绝热指数 =1.4,求:(1)终态参数 2 T 和 V2 ;(2)过程功和技术功;(3) U 和 H 。 提示和答案:绝热过程过程功和技术功分别等于热力学能减少量和焓减少量。 2 T 466.17K 、 3 2 v 1.3379m / kg 、W 934.47kJ 、 t W 1308.26kJ、 U 934.47kJ 、 H 1308.26kJ 。 4-6 同上题,比热容为变值,按空气热力性质表重新进行计算。 提示和答案:利用 2 r2 r1 1 p p p p 查附表 7 得 2 T ,进而查得 2 h ,不论比热容是否取定值, 绝热过程过程功和技术功分别等于热力学能减少量和焓减少量。 W 983.22kJ、 t W 1336.82kJ 。 4-7 1kg 空气初态为 1 p 0.5MPa , 1 T 1 000K ,按定熵过程:(1)变化到 2 T 500K, 试确定 2 p ;(2)变化到 2 p 0.1MPa 确定 2 T 。空气的 p c 可由空气真实热容公式确定: , m 3 6 9 12 2 3 4 K K K K 3.653 1.337 10 3.294 10 1.913 10 0.276 3 10 C p T T T T R 将计算结果与利用气体性质表求出的值进行比较。 提示和答案: (1)将 C p,m 代入 2 ,m 1 d ln 0 p T p S C R T p ,解得 2 p 0.037MPa ; (2) 同理有 2 2 ,m 1000K 1 d ln 0 T p T p C R T p ,用迭代法得出 2 T 657.4 K 。(a)根据 1 2 T T 、 , 查得 r1 r 2 p p 115.97 8.5558 , ,所以 r 2 2 1 r1 0.03689MPa p p p p ;(b)已知 1 1 2 p T p , , 得 r2 p 23.194 根据 pr2 ,查得 2 T 657.419K ,表明用真实比热容式积分所得的结果与气体性 质表得出的结果是一致的,但后一方法更方便

工程热力学第5版题解 4-8某气缸中空气初始参数p=8MP,t=1300℃,进行了一个可逆多变过程后, 终态P,=0.4MPa,52=400℃,空气的气体常数R=0.287kJ(kg·K),试按下列两种方法 计算空气该过程是放热还是吸热?(1)按定值比热容,C=0.718kJ/(kg·K):(2)比热 容是温度的线性函数{c,}uss,=0.7088+0.000186{c。 提示和答案:由pT:P2、T确定多变指数n=1.3955。(1) AM=c,G-D=-6462kg、w=nR-)=653.1We、g=△A+w=69%e 所以是吸格过程.(2)如-d=-网2g、=,低-T)=653he、 q=△+w=-127.1kJ/kg,放热过程。可见温度变化范围很大时按定值比热容计算误差太大。 4-9一体积为0.15m3的气罐,内装有p=0.55MPa,1=38℃的氧气,今对氧气 加热,其温度、压力都将升高,罐上装有压力控制阀,当压力超过0.7MP时阀门自动打 开,放走部分氧气,使罐中维持最大压力0.7MPa。问当罐中氧气温度为285℃时,共加 入多少热量?设氧气的比热容为定值,c=0.667kJ/kg·K),c。=0.917kJ/(kgK)。 提示和答案:初、终态氧气质量m==102kg、m==072kg·据题意1-2 RT RT 是定容加热过程,T=卫T=395.8K,Q,=mG,(,-T)=56.83kJ。2-3是边加热,边放 P 气的过程,过程中氧气压力不变,恒为0.7MP。罐中气体由m,(=m,)减少到m,温度由T, 升高到,任何中间状态都满足2y=mRI。g,三mc,7G灯r2719 Q=Q+Qn=184.02kJ。 4-10某理想气体在T-s图上的四种 过程如图4-2a所示,试在p-v图上画出相 应的四个过程,并对每个过程说明n的范围, 是吸热还是放热,是膨胀还是压缩过程? 提示和答案:各过程如图4-2。(1) (b) 图4-2 22
工程热力学第 5 版题解 22 4-8 某气缸中空气初始参数 1 1 p t 8MPa 1 300 C , ,进行了一个可逆多变过程后, 终态 2 2 p t 0.4MPa 400 C , ,空气的气体常数 g R 0.287kJ/(kg K) ,试按下列两种方法 计算空气该过程是放热还是吸热?(1)按定值比热容, 0.718kJ/(kg K) V c ;(2)比热 容是温度的线性函数 kJ/ ( kg K ) C 0.708 8 0.000 186 V c t 。 提 示 和 答 案 : 由 1 1 2 2 p T p T 、 ; 、 确 定 多 变 指 数 n 1.395 5 。( 1 ) 2 1 ( ) 646.2kJ/kg V u c T T 、 g 1 2 1 ( ) 653.1kJ/kg 1 w R T T n 、q u w 6.9kJ/kg 所以是吸热过程。(2) 2 1 d 780.21kJ/kg V u c t 、 g 1 2 1 ( ) 653.1kJ/kg 1 w R T T n 、 q u w 127.1kJ/kg ,放热过程。可见温度变化范围很大时按定值比热容计算误差太大。 4-9 一体积为 3 0.15 m 的气罐,内装有 1 1 p t 0.55 MPa 38 C , 的氧气,今对氧气 加热,其温度、压力都将升高,罐上装有压力控制阀,当压力超过 0.7 MPa 时阀门自动打 开,放走部分氧气,使罐中维持最大压力 0.7 MPa 。问当罐中氧气温度为 285 ℃时,共加 入多少热量?设氧气的比热容为定值, 0.667 kJ/(kg K) V c , 0.917 kJ/(kg K) p c 。 提示和答案: 初、终态氧气质量 1 3 1 3 g 1 g 3 1.02kg 0.72kg p V p V m m R T R T 、 。据题意 1-2 是定容加热过程, 2 2 1 1 395.8K p T T p , 1 2 1 ( ) 56.83kJ Q m c T T V V 。2-3 是边加热,边放 气的过程,过程中氧气压力不变,恒为 0.7MPa 。罐中气体由 2 1 m m ( ) 减少到 m3 ,温度由 2 T 升高到 3 T ,任何中间状态都满足 3 g p V mR T 。 3 2 3 g d d 127.19kJ T p p p T p V Q mc T c T R T , 184.02kJ Q Q Q V p 。 4-10 某理想气体在 T s 图上的四种 过程如图 4-2a 所示,试在 p v 图上画出相 应的四个过程,并对每个过程说明 n 的范围, 是吸热还是放热,是膨胀还是压缩过程? 提示和答案: 各过程如图 4-2。(1) (a) (b) 图 4-2
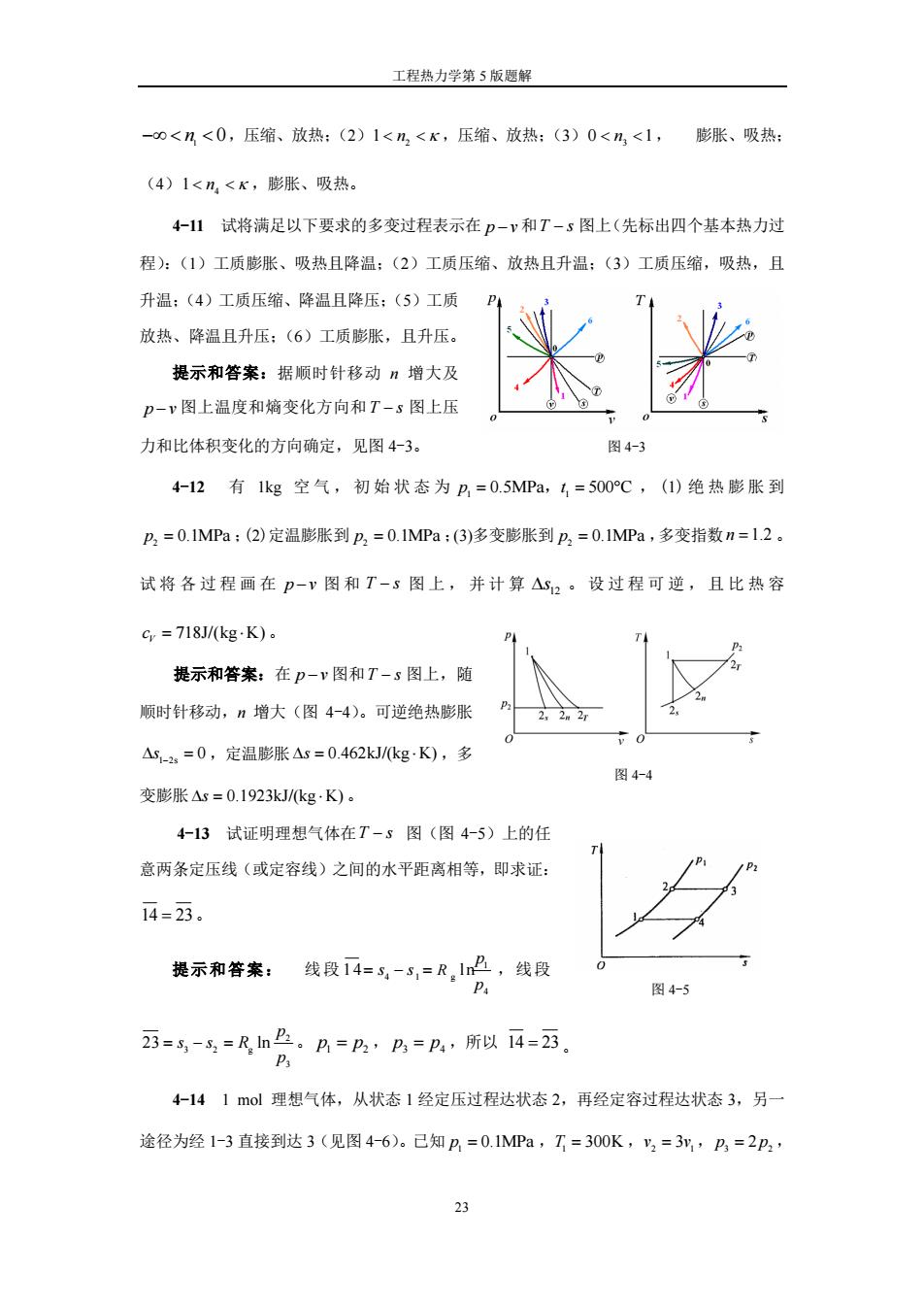
工程热力学第5版题解 -0<n<0,压缩、放热:(2)1<n2<K,压缩、放热:(3)0<n<1, 膨胀、吸热: (4)1<n,<K,膨胀、吸热。 4-11试将满足以下要求的多变过程表示在p-v和T-s图上(先标出四个基本热力过 程):(1)工质膨胀、吸热且降温:(2)工质压缩、放热且升温:(3)工质压缩,吸热,且 升温:(4)工质压缩、降温且降压:(5)工质 放热、降温且升压:(6)工质膨胀,且升压。 提示和答案:据顺时针移动n增大及 p-v图上温度和熵变化方向和T-s图上压 力和比体积变化的方向确定,见图4-3。 图4-3 4-12有1kg空气,初始状态为p=0.5MPa,t=500C,(1)绝热膨胀到 P2=0.1MPa:(2)定温膨胀到P,=0.1MPa:(3)多变膨胀到p,=0.1MPa,多变指数n=1.2。 试将各过程画在p-v图和T-5图上,并计算△S2。设过程可逆,且比热容 cr=718J/kg·K)。 提示和答案:在p-v图和T-s图上,随 顺时针移动,n增大(图4-4)。可逆绝热膨胀 2,2m27 △S-2s=0,定温膨胀△s=0.462kJ/kgK),多 图4-4 变膨胀△s=0.1923kJ/kg·K)。 4-13试证明理想气体在T-5图(图4-5)上的任 意两条定压线(或定容线)之间的水平距离相等,即求证: 14=23。 提示和答案: 线段14=5,-5,=R.1n凸,线段 P 图4-5 23=5-5,=RnB。A=P,P=p,所以14=23 P 4-141mol理想气体,从状态1经定压过程达状态2,再经定容过程达状态3,另一 途径为经1-3直接到达3(见图4-6)。己知p,=0.1MPa,T=300K,2=3y,P=2P2, 23
工程热力学第 5 版题解 23 图 4-5 n1 0 ,压缩、放热;(2) 2 1 n ,压缩、放热;(3) 3 0 1 n , 膨胀、吸热; (4) 4 1 n ,膨胀、吸热。 4-11 试将满足以下要求的多变过程表示在 p v 和 T s 图上(先标出四个基本热力过 程):(1)工质膨胀、吸热且降温;(2)工质压缩、放热且升温;(3)工质压缩,吸热,且 升温;(4)工质压缩、降温且降压;(5)工质 放热、降温且升压;(6)工质膨胀,且升压。 提示和答案:据顺时针移动 n 增大及 p v 图上温度和熵变化方向和 T s 图上压 力和比体积变化的方向确定,见图 4-3。 4-12 有 1kg 空 气 , 初 始 状 态 为 1 1 p t 0.5MPa 500 C , , (1) 绝 热 膨 胀 到 2 p 0.1MPa ;(2)定温膨胀到 2 p 0.1MPa ;(3)多变膨胀到 2 p 0.1MPa ,多变指数 n 1.2 。 试 将 各 过 程 画 在 p v 图 和 T s 图 上 , 并 计 算 12 s 。 设 过 程 可 逆 , 且 比 热 容 718J/(kg K) V c 。 提示和答案:在 p v 图和 T s 图上,随 顺时针移动,n 增大(图 4-4)。可逆绝热膨胀 1 2s s 0 ,定温膨胀 s 0.462kJ/(kg K) ,多 变膨胀 s 0.1923kJ/(kg K) 。 4-13 试证明理想气体在 T s 图(图 4-5)上的任 意两条定压线(或定容线)之间的水平距离相等,即求证: 14 23 。 提示和答案: 线段 1 4 1 g 4 14 ln R p s s p ,线段 2 3 2 g 3 23 ln p s s R p 。 1 2 p p , 3 4 p p ,所以 14 23 。 4-14 1 mol 理想气体,从状态 1 经定压过程达状态 2,再经定容过程达状态 3,另一 途径为经 1-3 直接到达 3(见图 4-6)。已知 1 p 0.1MPa , 1 T 300K , 2 1 v v 3 , 3 2 p p 2 , 图 4-4 图 4-3

工程热力学第5版题解 试证明:(1)Q2+Q23≠93:(2)AS2+△S23=AS。 提示和答案:(1)分别列出两条途径的热力学第一定 律表达式,由于热力学能只是温度的函数,故证明他们的功不 等(如从过程线与v轴包围的面积)即可:(2)求出定压过程 图4-6 和定容过程熵变相加与△S-:比较。 4-15试导出理想气体定值比热容时多变过程熵差的计算式为 马-=n-大Rn (a) n(k-1) 或 5-5=0-Rn3 (n≠1) (b) (n-1)(x-1)T 并根据式(a)对图4-7中示出的三种压缩过程进行分析,它们 的n是大于、等于K,还是小于x?它们各是吸热、绝热、 图4-7 还是放热过程? 提示和答案: 将多变过程比热容C,-?ca上)代入A=了9-7 并注意 n-1 a-1 到,=K R和2 即证。过程线与s轴所夹的面积代表热量,由图分析熵变, 过程I是吸热过程,n>k或n<0:过程Ⅱ与s轴垂直,是可逆绝热过程,FK:过程Ⅲ 是放热过程,多变指数应满足0<n<K。 4-16气缸活塞系统的缸壁和活塞均为刚性绝热材料制成,如图4-8。A侧为N2,B侧 为O,,两侧温度、压力、体积均相同:TA,=T,=300K, 0 Pa1=Pa1=0.1MPa,'A='1=0.5m3。活塞可在气缸中无磨 擦地自由移动。A侧的电加热器通电后缓缓对N,加热,直到 图4-8 PA2=0.22MPa,设O2和N2均为理想气体,试按定值比热容计算:(1)T,和:(2)' 和T:(3)Q和W(A侧N2对B侧O2作出的功):(4)△S。和△S.:(5)在p-v图 及T-3图上定性地表示A、B两侧气体所进行的过程:(6)A侧进行的是否是多变过程, 为什么? 24
工程热力学第 5 版题解 24 图 4-6 图 4-7 图 4-8 试证明:(1) Q Q Q 12 23 13 ;(2) 12 23 13 S S S 。 提示和答案: (1)分别列出两条途径的热力学第一定 律表达式,由于热力学能只是温度的函数,故证明他们的功不 等(如从过程线与 v 轴包围的面积)即可;(2)求出定压过程 和定容过程熵变相加与 1 3 S 比较。 4-15 试导出理想气体定值比热容时多变过程熵差的计算式为 2 2 1 g 1 ln ( 1) n p s s R n p (a) 或 g 2 2 1 1 ( ) ln ( 1) ( 1)( 1) n R T s s n n T (b) 并根据式(a)对图 4-7 中示出的三种压缩过程进行分析,它们 的 n 是大于、等于 ,还是小于 ?它们各是吸热、绝热、 还是放热过程? 提示和答案: 将多变过程比热容 ( 1) 1 n V n c c n n 代入 δq c Td s T T ,并注意 到 g 1 1 V c R 和 1 2 2 1 1 n T p n T p 即证。过程线与 s 轴所夹的面积代表热量,由图分析熵变, 过程 I 是吸热过程, n 或 n 0 ;过程Ⅱ与 s 轴垂直,是可逆绝热过程,n= ;过程Ⅲ 是放热过程,多变指数应满足 0 n 。 4-16 气缸活塞系统的缸壁和活塞均为刚性绝热材料制成,如图 4-8。A 侧为 N2 ,B 侧 为 O2 ,两侧温度、压力、体积均相同: A1 B1 T T 300K , A1 B1 p p 0.1MPa , 3 A1 B1 V V 0.5m 。活塞可在气缸中无磨 擦地自由移动。A 侧的电加热器通电后缓缓对 N2 加热,直到 A2 p 0.22MPa ,设 O2 和 N2 均为理想气体,试按定值比热容计算:(1) B2 T 和 B2 V ;(2) VA2 和 A2 T ; (3) Q 和 WA (A 侧 N2 对 B 侧 O2 作出的功);(4) O 2 S 和 N2 S ;(5)在 p v 图 及 T s 图上定性地表示 A、B 两侧气体所进行的过程;(6)A 侧进行的是否是多变过程, 为什么?

工程热力学第5版题解 提示和答案:(1)活塞是自由的,故P2=P42。B内可逆绝热过程,T2=375.8K、 Va2=0.2847m3:(2)总体积不变,V2=0.7153m3、Tn=94.15K:(3)取A+B为热力 系,系统不作功Q=299.99kJ,取B为热力系,绝热,W。=-△U。=-31.58k且 W=-W。=31.58k:(4)△S。,=0、△S,=74k/K:(5),(6)略。 4-17空气装在如图4-9所示的绝热刚性气缸活塞装置内,气缸中间有一块带有小孔的 导热隔板,两活塞联动,故活塞移动时装置内总体积不变。设活塞移动时外界机器以对系统 作功40kJ,活塞与隔板静止后,系统恢复平衡。已知初始状态,p=2.0MPa,T=400K, 空气总质量m=2kg。设比热容为定值, c=0.718kJkg·K)。求:(1)终态空气的温度T2和压力 W=40 kJ p2:(2)系统的熵变△S12,是定熵过程吗?(3)在T-s 图4-9 图上示意性地画出该过程。 提示和答案:(1)Vh=V=0.0574m3。取A+B为系统,W=-(U+AU)=2c,(G-T), T3=T+=427.9K,p2 mcy mR=2139MPa。(2)过程中系统 2V, AS=mGln2+Rn =c,n三=00968J水>0,所以不是定箱过程。(3)略。 4-18 一孤立系统由带有活塞的气缸组成,活塞将气缸分成两部分,一侧装有理想气体 氢,气体常数R=2.077kJ/kgK),比热容c=3.116kJ/kgK),另一侧完全真空,内装 有一弹簧,弹性系数k=900N/m,弹簧的自由长度为0.3m,弹性力F=c,x表示伸长 或压缩的长度,初始位置如图4-10所示。初态为1=40C,V=10m3,p,=0.14MPa, 弹簧长度为0.25m。开始时活塞由销子固定,现拔去销子,则 气体和弹簧达到新的力平衡。假定不计活塞质量,且活塞是绝 真空 00000000 热的,面积A=0.001m2。不计移动磨擦阻力,求:力平衡 2ZZ2 时气体的压力和温度,状态变化前后气体的熵变,是否是定熵 025m 过程?试在T-s图上示意性地画出该过程。 图4-10 提示和答案:取弹簧自由伸长位置为坐标原点,x=0.3m-0.25m=0.05m, 25
工程热力学第 5 版题解 25 图 4-9 图 4-10 提示和答案:(1)活塞是自由的,故 B A 2 2 p p 。B 内可逆绝热过程, ,2 TB 375.8K 、 3 ,2 VB 0.2847m ;(2)总体积不变, 3 ,2 VA 0.7153m 、 2 TA 944.15K ;(3)取 A+B 为热力 系,系统不作功 Q 299.99kJ ,取 B 为热力系,绝热, 31.58kJ W U B B 且 A B W W 31.58kJ ;(4) O 2 S 0 、 N 2 S 74kJ/K ;(5),(6)略。 4-17 空气装在如图 4-9 所示的绝热刚性气缸活塞装置内,气缸中间有一块带有小孔的 导热隔板,两活塞联动,故活塞移动时装置内总体积不变。设活塞移动时外界机器以对系统 作功 40 kJ,活塞与隔板静止后,系统恢复平衡。已知初始状态, 1 p 2.0 MPa , 1 T 400 K, 空 气 总 质 量 m 2 kg 。 设 比 热 容 为 定 值 , 0.718 kJ/(kg K) V c 。求:(1)终态空气的温度 T2和压力 p2 ;(2)系统的熵变 S12 ,是定熵过程吗?(3)在 T s 图上示意性地画出该过程。 提示和答案:(1) 3 1 1 V V A B 0.0574m 。取 A+B 为系统, 1 2 ( ) 2 ( ) W U U c T T A B V , 2 1 427.9K V W T T mc , g 2 2 2.139MPa 2 A mR T p V 。 ( 2 ) 过 程 中 系 统 2 2 2 g 1 1 1 ln ln ln 0.0968kJ/K 0 V V T V T S m c R mc T V T ,所以不是定熵过程。(3)略。 4-18 一孤立系统由带有活塞的气缸组成,活塞将气缸分成两部分,一侧装有理想气体 氦,气体常数 g R 2.077 kJ/(kg K) ,比热容 3.116kJ/(kg K) V c ,另一侧完全真空,内装 有一弹簧,弹性系数 k 900N/m ,弹簧的自由长度为 0.3 m,弹性力 F kx ,x 表示伸长 或压缩的长度,初始位置如图 4-10 所示。初态为 1 t 40 C, 4 3 1 V 10 m , 1 p 0.14MPa , 弹簧长度为 0.25 m。开始时活塞由销子固定,现拔去销子,则 气体和弹簧达到新的力平衡。假定不计活塞质量,且活塞是绝 热的,面积 2 A 0.001 m 。不计移动磨擦阻力,求:力平衡 时气体的压力和温度,状态变化前后气体的熵变,是否是定熵 过程?试在 T s 图上示意性地画出该过程。 提 示和 答案 : 取弹簧自由伸长位置为 坐标原点, 1 x 0.3m 0.25m 0.05m

工程热力学第5版题解 m=P些=02154x10kg·初态弹簧压力n,-三=位=0.045MPa0, 是非定熵绝热过程。 4-19一竖直气缸截面积A=6450m2,内置一重100N活塞,通过管道、阀门与气源 相通。如图4-11,起初活塞在气缸底部,打开阀门空气缓缓流入,当活塞上移至L=0.6m时 阀门关闭,这时气缸内空气温度为30℃,已知输气管中空气参数保 100N 持一定,PL=0.15MP阳,1=90℃。活塞与缸壁间无磨擦损失, 大气压力P。=0.1013MPa,求:(1)气缸内气体的终态压力p:(2) 对外作出的功W:(3)过程中气体对外作出的有用功W。;(4)吸 ⑧u IL=90 C.PL=0.15 MPa 热量Q。已知c=718J/kg·K),c。=1005J/kg·K)。 图4-11 F 提示和答案:(1)气缸内气体压力p=P。+ =0.1168MPa:(2)空气对外作功, A W=∫pV=0.452k(3)输出的有用功m=FL=0.06k:(4)由非稳定流动能量方程 δQ=dU+hδmn+δW,考虑到δmn=dm,m,=m。,m= W=0.0052kg、 RT Q=-0.313kJ。 4-20容器A中装有0.2kg的一氧化碳C0,压力为0.07MPa、温度为77℃。容器B 中装有0.8kg压力为0.12MPa、温度为27℃的C0见图4-25。A和B的壁面均为透热壁面, 26
工程热力学第 5 版题解 26 图 4-11 1 1 4 g 1 0.2154 10 kg p V m R T 。初态弹簧压力 1 1 0 1 0.045MPa F kx p p A A 。设中间状态氦 气体积为 V, 1 1 F kx k V V p x A A A A ,代入数据得 3 8 4 Pa m p V 9 10 4.5 10 (a) 取氦气为热力系,是绝热系,能量方程 δW U d 即 d dV p V mc T 。中间状态 8 4 p 910 V 4.510 ,所以代入后两边积分后得: 8 2 4 2 2 2 T V V 313 67.064 10 67.064 10 (b) 将式(a)、(b)代入 2 2 g 2 p V m R T ,经整理可解得 4 3 2 V 1.4369 10 m ,代入式(a)、(b)得 2 p 0.0843MPa、 2 T 270.89K 、 2 2 4 g 1 2 1 1 ln ln 0.0652 10 kJ/K 0 V T V S m c R T V , 是非定熵绝热过程。 4−19 一竖直气缸截面积 2 A 6 450mm ,内置一重 100N 活塞,通过管道、阀门与气源 相通。如图 4-11,起初活塞在气缸底部,打开阀门空气缓缓流入,当活塞上移至 L 0.6m 时 阀门关闭,这时气缸内空气温度为 30℃,已知输气管中空气参数保 持一定, L p 0.15MPa , L t 90 C 。活塞与缸壁间无磨擦损失, 大气压力 0 p 0.101 3MPa ,求:(1)气缸内气体的终态压力 p;(2) 对外作出的功 W;(3)过程中气体对外作出的有用功 W u ;(4)吸 热量 Q。已知 718 J/(kg K) 1 005 J/(kg K) V p c c , 。 提示和答案:(1)气缸内气体压力 0 0.1168MPa F p p A ;(2)空气对外作功, 2 1 W p V d 0.452kJ ;(3)输出的有用功 u W FL 0.06kJ ;(4)由非稳定流动能量方程 in in i δQ U h m W d δ δ ,考虑到 in δm m d , m m 2 in , 2 2 2 g 2 0.0052kg p V m R T 、 Q 0.313kJ 。 4−20 容器 A 中装有 0.2 kg 的一氧化碳 CO,压力为 0.07MPa 、温度为 77℃。容器 B 中装有 0.8 kg 压力为 0.12MPa 、温度为 27℃的 CO 见图 4-25。A 和 B 的壁面均为透热壁面

工程热力学第5版题解 之间用管道和阀门相通,现打开阀门,CO气体由B流向A, CO 若压力平衡时温度同为1,=42℃,C0为理想气体,试求:(1) CO 8kg 0.2kg 0.12 MPa 0.07 MPa 平衡时终压p2:(2)吸热量Q。过程中平均比热容 77℃ 27℃ c=0.745kJ/kgK)。 提示和答案:取A+B为热力系,总质量和总容积不变, 图4-12 对终态写出状态方程,得卫,=0.105MPa:由闭口系能量方程求得Q=3.725kJ。 421有一刚性绝热容器被绝热隔板一分为二,V=。=28×103m,A中装有 0.7MPa65°(的氧气,B为真空,见图4-13。打开安装在隔 板上的阀门,氧气自A流向B,两侧压力相同时关闭阀门。试 0.7 MPa 65℃ 求:(1)终压P,和两侧终温T2和T2:(2)过程前后氧气的熵 变△S2,设氧气的c。=0.920kJ/kgK)。 图4-13 提示和答案:(1)终态时两侧O2质量即初态A侧质量, 会'+n日5223,考虑到终态压力Pn=Pm,所以 m寸mRT:RTa: 2.07×10 (a) A侧为绝热放气,其中气体经历等比熵过程,参数变化规律 Pm=0.9860×103T35 (b) 取A和B为热力系,是不作外功的绝热闭口系 4.48m42(T2-T2)+T2=338 (c) 而 me=0.10627×10Ta25 (d) 采用迭代方法(a)(b)(c)(d)四式联解求得p2=0.35MPa:T2=277.3K,T2=432.72K。 (2)熵变△S,=0.0352kJ/K。 4-22空气瓶内装有2=3.0MP,T=296K的高压空气,可驱动一台小型气轮机, 用作发动机的起动装置,如图4-14所示。要求该气轮机能产生5kW的平均输出功率,并持 续半分钟而瓶内空气压力不得低于0.3MP。设气轮机中进行的是可逆绝热膨胀过程,气轮 2>
工程热力学第 5 版题解 27 图 4-12 图 4-13 之间用管道和阀门相通,现打开阀门,CO 气体由 B 流向 A, 若压力平衡时温度同为 2 t 42 C,CO 为理想气体,试求:(1) 平 衡 时终 压 2 p ;( 2) 吸热 量 Q 。过 程中 平均比 热 容 0.745 kJ/(kg K) V c 。 提示和答案: 取 A+B 为热力系,总质量和总容积不变, 对终态写出状态方程,得 2 p 0.105MPa ;由闭口系能量方程求得 Q 3.725kJ 。 4−21 有一刚性绝热容器被绝热隔板一分为二, 3 3 A B V V 28 10 m ,A 中装有 0.7 MPa 65 C 、 的氧气,B 为真空,见图 4-13。打开安装在隔 板上的阀门,氧气自 A 流向 B, 两侧压力相同时关闭阀门。试 求:(1)终压 p2 和两侧终温 TA2 和 B2 T ;(2)过程前后氧气的熵 变 12 S ,设氧气的 0.920 kJ/(kg K) p c 。 提示和答案: ( 1 ) 终 态 时 两 侧 O2 质量即初态 A 侧质量, A2 A B2 B A1 A A2 B2 A1 g A2 g B2 g A1 0.2232kg p V p V p V m m m R T R T R T ,考虑到终态压力 A B 2 2 p p ,所以 3 2 2 2 1 1 2.07 10 A A B p T T (a) A 侧为绝热放气,其中气体经历等比熵过程,参数变化规律 1 2 3 3.5 2 1 2 1 0.9860 10 A A A A A T p p T T (b) 取 A 和 B 为热力系,是不作外功的绝热闭口系 2 2 2 2 4.48 ( ) 338 m T T T A A B B (c) 而 6 2.5 2 2 0.10627 10 m T A A (d) 采用迭代方法(a)(b)(c)(d)四式联解求得 2 0.35MPa A p ; 2 TA 277.3K , 2 TB 432.72K 。 (2)熵变 12 S 0.0352kJ/K 。 4−22 空气瓶内装有 1 1 p T 3.0MPa 296K , 的高压空气,可驱动一台小型气轮机, 用作发动机的起动装置,如图 4-14 所示。要求该气轮机能产生 5kW 的平均输出功率,并持 续半分钟而瓶内空气压力不得低于 0.3MPa 。设气轮机中进行的是可逆绝热膨胀过程,气轮

工程热力学第5版题解 机出口排气压力保持一定p,=0.lMPa。空气瓶是绝热的,不计 算管路和阀门的摩阻损失。问空气瓶的体积V至少要多大? P:3 MPa 提示和答案:初态气瓶内空气质量m= P =35.314V。 T-296K RT Po-0.I MPa 打开阀门绝热放气,瓶中剩余气体的参数按等比熵过程变化, x-l 图4-14 T=153.31K 终态气瓶内空气质量 m=pV =6.818Ψ RT 流出的空气 -△m=m-m2=35.314V-6.818V=28.496/ -1 放气过程气瓶内任何中间状态P2、T,都有T T,若不计磨擦损失,气轮机入口 K-l 参数与气瓶内放气参数P2、T,时刻相同。任一时刻气轮机内,T4=T 气轮机入 口参数为p2、T,气轮机出口参数为p,=0.1MPa、T, =112.01K 整个放气过程气轮机出口压力、温度保持为0.1MPa、112.01K。 取气瓶和涡轮机一起为热力系,能量方程δQ=dU+hδmut-h.δmm+δW:,积分得 m3,-m7-TAm+亚=0。代入已知数据,解得r0O43m. 4-23某锅炉每小时生产10000kg表压力为p。=1.9MPa,温度1=350C的蒸汽。设 锅炉给水温度为1,=40℃,锅炉效率7。=0.78。煤的发热量(热值)为Qp=2.97×10kJkg。 求每小时锅炉的煤耗量是多少?汽锅内水的加热和汽化、以及蒸汽的过热都在定压下进行。 锅炉效率的定义为: 水和蒸汽所吸的热量 To= 燃料燃烧时所在发出的热量 (未被水和蒸汽所吸收的热量是锅炉的热损失,其中主要是烟囱出口处排烟所带走的热量。) 28
工程热力学第 5 版题解 28 机出口排气压力保持一定 b p 0.1MPa 。空气瓶是绝热的,不计 算管路和阀门的摩阻损失。问空气瓶的体积 V 至少要多大? 提示和答案:初态气瓶内空气质量 1 1 g 1 35.314 p V m V R T 。 打开阀门绝热放气,瓶中剩余气体的参数按等比熵过程变化, 1 2 2 1 1 153.31K p T T p 终态气瓶内空气质量 2 2 g 2 6.818 p V m V R T 流出的空气 1 2 m m m V V V 35.314 6.818 28.496 放气过程气瓶内任何中间状态 2 p 、T2 都有 1 2 2 1 1 p T T p ,若不计磨擦损失,气轮机入口 参数与气瓶内放气参数 2 p 、T2 时刻相同。任一时刻气轮机内, 1 4 4 3 3 p T T p ,气轮机入 口参数为 2 p 、T2 ,气轮机出口参数为 4 4 p T 0.1MPa、 , 1 1 1 1 4 4 2 4 4 4 3 2 1 1 3 3 1 3 1 112.01K p p p p p T T T T T p p p p p 整个放气过程气轮机出口压力、温度保持为 0.1MPa 、112.01K 。 取气瓶和涡轮机一起为热力系,能量方程 out out in in i δQ U h m h m W d δ δ δ ,积分得 2 2 1 1 4 0 i V W m T m T T m c 。代入已知数据,解得 3 V 0.043m 。 4-23 某锅炉每小时生产 10 000kg 表压力为 e p 1.9MPa ,温度 1 t 350 C 的蒸汽。设 锅炉给水温度为 2 t 40 C ,锅炉效率 B 0.78 。煤的发热量(热值)为 4 2.97 10 kJ/kg QP 。 求每小时锅炉的煤耗量是多少?汽锅内水的加热和汽化、以及蒸汽的过热都在定压下进行。 锅炉效率 B 的定义为: B 水和蒸汽所吸的热量 燃料燃烧时所在发出的热量 (未被水和蒸汽所吸收的热量是锅炉的热损失,其中主要是烟囱出口处排烟所带走的热量。) 图 4-14

工程热力学第5版题解 提示和答案:生产蒸汽需要吸入热量q。=q9,每小时锅炉耗煤 m=6=1281k. nOp 4-241kg蒸汽,p=3MPa、t=450C,可逆绝热膨胀至P,=0.004MPa,试用h-s 图求终点状态参数,、y2h、S,并求膨胀功和技术功。 提示和答案:由h-s图查得:h=3345kJ/g、y=0.108m3/kg、 S=7.082kJ/kgK):h=2132kJ/g、2=28m3/kg、S2=3=7.082kJ/kgK)、 1,=29.4C。绝热过程膨胀功等于热力学能差,w=1001kJg,技术功等于焓差, m,=1214kJ/kg。 4-251kg蒸汽,由初态P,=2MPa,x=0.95,定温膨胀到p,=1MPa,求终态参数 122h,、S2及过程中对蒸汽所加入的热量q和过程中蒸汽对外界所作的膨胀功w。 提示和答案:由h-s图查得h、s及h,=2861k/g、t,=212.5C、 y,=0.215mkg和32=6.760kJ/kgK),据第一定律解析式,分别求出热量和热力学能差 即可求得功,而定温过程q=T(s2-S)=299.2kJkg、w=q-△u=169.2kJkg。 4-26一台功率为20000kW的汽轮机,其耗汽率为d=1.32×10~6kgJ。从汽轮机排出 的乏气参数为p,=0.004MPa、x,=0.9。乏汽进入冷凝器 冷却水 后凝结为冷凝水,如图4-15所示。冷凝器中的压力设为 出口 冷却水 0.004MPa,即等于乏汽压力。冷凝水的温度等于乏汽压力 下的饱和温度,乏汽在凝结时放出热量。这些热量为冷却水 凝销水 图4-15 所吸收,因此冷却水离开冷凝器时的温度高于进入时的温 度。设冷却水进入冷凝器时的温度为10℃,离开时温度为18℃,求冷却水每小时的流量 (th)。冷却水在管内流动,乏汽在管壁外凝结。管子通常用黄铜管,大型冷凝器中装有数 千根黄铜管。 提示和答案:已知功率及汽耗率可得每小时耗汽量,由乏汽状态可查取汽化潜热,得 乏汽凝结为饱和水时放热量,再以冷凝器为体系,列能量方程解得冷却水流qm=6221.4Th。 29
工程热力学第 5 版题解 29 图 4-15 提 示 和 答 案 : 生 产 蒸 汽 需 要 吸 入 热 量 Q m q q q , 每小时锅炉耗煤 B 1 281 kg/h Q p q m Q 。 4-24 1 kg 蒸汽, 1 1 p t 3MPa 450 C 、 ,可逆绝热膨胀至 2 p 0.004MPa ,试用 h s 图求终点状态参数 2 2 2 2 t v h s 、 、 、 并求膨胀功和技术功。 提 示 和 答 案 : 由 h s 图 查 得 : 1 h 3345kJ/kg 、 3 1 v 0.108m / kg 、 1 s 7.082kJ/(kg K) ; 2 h 2132kJ/kg 、 3 2 v 28m /kg 、 2 1 s s 7.082kJ/(kg K) 、 2 t 29.4 C 。绝热过程膨胀功等于热力学能差, w 1001kJ/kg ,技术功等于焓差, t w 1214kJ/kg 。 4-25 1 kg 蒸汽,由初态 1 p 2MPa , 1 x 0.95 ,定温膨胀到 2 p 1MPa ,求终态参数 2 2 2 2 t v h s 、 、 、 及过程中对蒸汽所加入的热量 T q 和过程中蒸汽对外界所作的膨胀功 w。 提示和答案: 由 h s 图查得 1 1 1 h v s 、 、 及 2 h 2861kJ/kg 、 2 t 212.5 C 、 3 2 v 0.215m /kg 和 2 s 6.760kJ/(kg K) ,据第一定律解析式,分别求出热量和热力学能差 即可求得功,而定温过程 2 1 ( ) 299.2kJ/kg T q T s s 、 169.2kJ/kg w q u T 。 4-26 一台功率为 20 000 kW 的汽轮机,其耗汽率为 d =1.32×10 - 6 kg/J。从汽轮机排出 的乏气参数为 2 2 p x 0.004 MPa 0.9 、 。乏汽进入冷凝器 后凝结为冷凝水,如图 4-15 所示。冷凝器中的压力设为 0.004 MPa ,即等于乏汽压力。冷凝水的温度等于乏汽压力 下的饱和温度,乏汽在凝结时放出热量。这些热量为冷却水 所吸收,因此冷却水离开冷凝器时的温度高于进入时的温 度。设冷却水进入冷凝器时的温度为 10 ℃,离开时温度为 18 ℃,求冷却水每小时的流量 (t/h)。冷却水在管内流动,乏汽在管壁外凝结。管子通常用黄铜管,大型冷凝器中装有数 千根黄铜管。 提示和答案: 已知功率及汽耗率可得每小时耗汽量,由乏汽状态可查取汽化潜热,得 乏汽凝结为饱和水时放热量,再以冷凝器为体系,列能量方程解得冷却水流 6221.4T/h m q