
山西破源宇院 SHANXI INSTITUTE OF ENEROY 第六章 单相对流换热的实验关联式 1
第六章 单相对流换热的实验关联式 1

山西限源宇院 SHANXI INSTITUTE OF ENEROY 6.1相似原理与量纲分析 实验是一个重要的手段。 相似原理指导下的实验研究仍然是解决复杂对 流换热问题的可靠方法。 相似原理回答三个问题 : (1)如何安排实验? (2)如何整理实验数据? (3)如何推广应用实验研究结果? 2
2 6.1 相似原理与量纲分析 实验是一个重要的手段。 相似原理指导下的实验研究仍然是解决复杂对 流换热问题的可靠方法。 相似原理回答三个问题: (1)如何安排实验? (2)如何整理实验数据? (3)如何推广应用实验研究结果?

山西破源宇花 SHANXI INSTITUTE OF ENEROY 相似原理主要包含以下内容: (1)物理现象相似的定义 (2)物理现象相似的性质 (3)相似特征数之间的关系 (4)物理现象相似的条件 第五章对流换热 3
第五章 对流换热 3 相似原理主要包含以下内容: (1)物理现象相似的定义 (2)物理现象相似的性质 (3)相似特征数之间的关系 (4)物理现象相似的条件

山西移源宇院 SHANXI INSTITUTE OF ENEROY 6.1.1 物理现象相似的定义 如果同类物理现象之间所有同名物理量场都相似 即同名的物理量在所有对应时间、对应地点的数值成 比例,则称物理现象相似。 同类物理现象:具有相同性质、服从于同一自然规律、 用形式和内容相同的方程式来描写的物理现象。 相似:对于同类的物理现象,在相应的时刻与相应的 地点上与现象有关的物理量一一对应成比例。 4
6.1.1 物理现象相似的定义 4 如果同类物理现象之间所有同名物理量场都相似, 即同名的物理量在所有对应时间、对应地点的数值成 比例,则称物理现象相似。 同类物理现象:具有相同性质、服从于同一自然规律、 用形式和内容相同的方程式来描写的物理现象。 相似:对于同类的物理现象,在相应的时刻与相应的 地点上与现象有关的物理量一一对应成比例

山西限源宇院 SHANXI INSTITUTE OF ENEROY 如果物理现象由 ?4,Pg,PC,…物理量来描述 ,则彼此 相似的物理现象就有个对应相似的物理量场,即在所 有对应的时间和对应的地点 B B 其中 各物理量的相似倍数。如果所有的 相似倍数等于1,则两个物理现象完全相同。 第五章对流换热 5
第五章 对流换热 5 如果物理现象由 等n个物理量来描述,则彼此 相似的物理现象就有n个对应相似的物理量场,即在所 有对应的时间和对应的地点, , , , A B C , A A A C = , B B B C = , C C C C = 其中 分别为各物理量的相似倍数。如果所有的 相似倍数都等于1,则两个物理现象完全相同。 , , , A B C C C C

山多能源宇花 HANXI IN TITUT老OF ENEROY 对应时间:指时间坐标对应成比例的时间,也称相似 时间。 t' t圪 t ts T x数 ty Ty T” 0 0.25 0.5 0.75 1.0 0 0.250.5 0.751.0 _ T' t; 式中C,夕时间坐标比例常数,或称为时间相似倍数。 如果分别采用无量纲时间坐标 '/T',x"/T"应时间的 无量纲时间坐标分别相等。 6
6 对应时间:指时间坐标对应成比例的时间,也称相似 时间。 1 2 3 1 2 3 T C T = = = = = 式中 C 为时间坐标比例常数,或称为时间相似倍数。 如果分别采用无量纲时间坐标 ,则对应时间的 无量纲时间坐标分别相等。 / , / T T
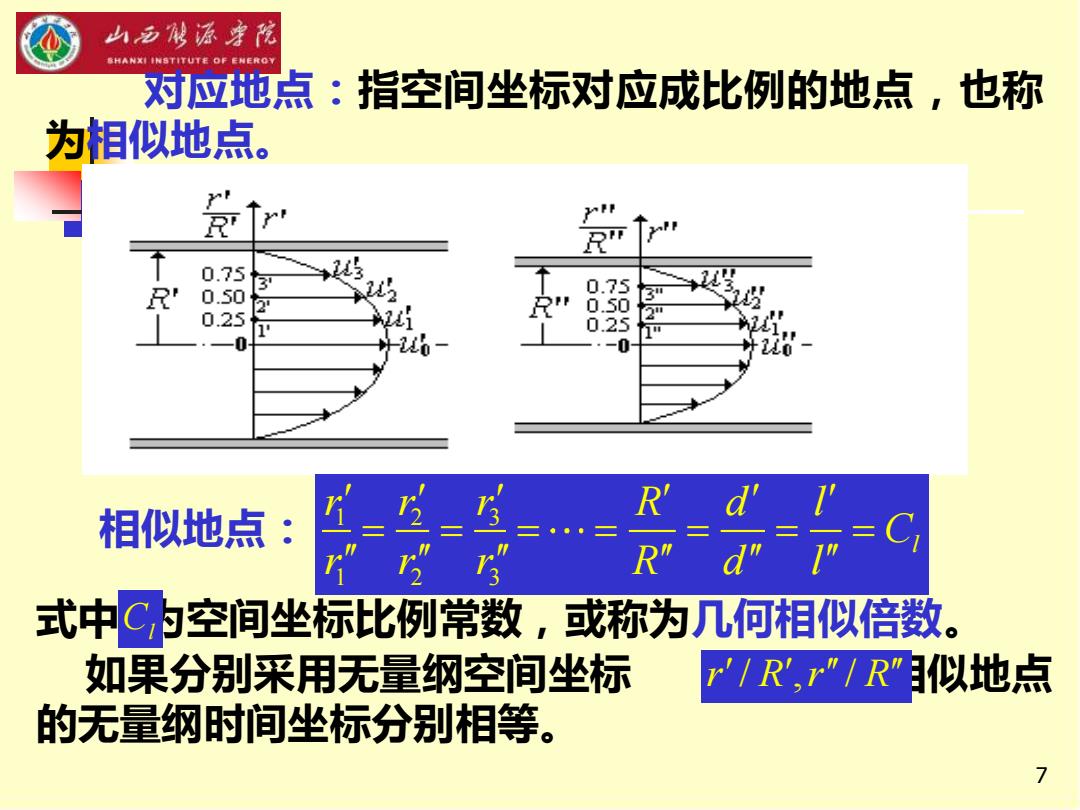
山五限源宇花 SHANXI INSTITUTE OF ENEROY 对应地点:指空间坐标对应成比例的地点,也称 为相似地点。 0.75 23 R 0.50 0.75 0.25 R” 0.50 0.25 -0 26- Rd′ 相似地点: ”” R”d" 式中C,为空间坐标比例常数,或称为几何相似倍数。 如果分别采用无量纲空间坐标 r'/R',r"/R”似地点 的无量纲时间坐标分别相等。 7
7 对应地点:指空间坐标对应成比例的地点,也称 为相似地点。 1 2 3 1 2 3 l r r R d l r C r r r R d l = = = = = = = 式中 C 为空间坐标比例常数 l ,或称为几何相似倍数。 如果分别采用无量纲空间坐标 ,则相似地点 的无量纲时间坐标分别相等。 r R r R / , / 相似地点:

山西破源宇花 SHANXI INSTITUTE OF ENEROY 两个管内稳态层流速度场相似以,所有相似地点的速度 成比例, u 24” u, u, 式中C的速度相似倍数。如果采用无量纲速度 4-4尘_-4 无量纲速 4644 401401u0 度场相同 结论:相似物理现象的所有同名无量纲物理量场相同。 8
8 两个管内稳态层流速度场相似,所有相似地点的速度 成比例, 1 2 3 0 1 2 3 0 u u u u u C u u u u = = = = 式中 C 为 u 速度相似倍数。 0 如果采用无量纲速度 u u/ , 1 1 2 2 3 3 0 0 0 0 0 0 , , , u u u u u u u u u u u u === 无量纲速 度场相同 结论:相似物理现象的所有同名无量纲物理量场相同

山西佛源宇花 SHANXI INSTITUTE OF ENEROY 凡是相似的物理现象,其物理量的场一定 可用一个统一的无量纲的场来表示。 0 1.0 n=r/R 农 9
9 凡是相似的物理现象,其物理量的场一定 可用一个统一的无量纲的场来表示

山西限源宇院 SHANXI INSTITUTE OF ENEROY 6.1.2相似原理的基本内容 一、 相似性质 彼此相似的现象,它们的同名相似准则必定相等 导出相似准测(特征数) 的两种方法: (1)相似分析法:数学模型无量纲化,P233非稳态导热 相似倍数 (2)量纲分析法 第五章对流换热 10
6.1.2 相似原理的基本内容 一、相似性质 彼此相似的现象,它们的同名相似准则必定相等 导出相似准则(特征数)的两种方法: (1)相似分析法:数学模型无量纲化,P233非稳态导热 相似倍数 (2)量纲分析法 第五章 对流换热 10