山西能源学院：《传热学》课程教学资源（PPT课件）第十章 传热过程分析与换热器的热计算（2/2）

山西限源宇院 SHANXI INSTITUTE OF ENEROY 10-4间壁式换热器的热计算 换热器热计算分两种情况：设计计算和校核计算 ()设计计算：根据生产任务给定的换热条件和要求，确定换热 器的型式、面积及结构参数 (2)校核计算：对已有或已选定的换热器，在非设计工况条件 下，核算它能否满足换热要求。一般是校核出口温度和换热量 能否达到要求 换热器热计算的基本方程式是传热方程式及热平衡式 Φ=kA△tm Th (Hot) D=gmiCh(th-th)=gmece(te-te) T(cold)

10-4 间壁式换热器的热计算 换热器热计算分两种情况：设计计算和校核计算 (1) 设计计算:根据生产任务给定的换热条件和要求，确定换热 器的型式、面积及结构参数 (2) 校核计算：对已有或已选定的换热器，在非设计工况条件 下，核算它能否满足换热要求。一般是校核出口温度和换热量 能否达到要求 换热器热计算的基本方程式是传热方程式及热平衡式 m  = kAt ( ) ( ) mh h h h mc c c c  = q c t −t = q c t−t x T Th (Hot) Tc (cold) T1 T2 ' h t " h t ' c t " c t

山多能源宇花 SHANXI INSTITUTE OF ENEROY 式中，△1m不是独立变量，因为它取决于t%,t%,t,以及换热 器的布置。另外，根据公式(10-15)可是，一旦9mhCh和AmcCe 以及%，%，，公中的三个已知的话，我们就可以计算出另外一 个温度。因此，上面的三个方程中共有8个未知数，即 Φ，k,A,9mbCh,9mcCe,以及t%,t公t中的三个 需要给定其中的5个变量，才可以计算另外三个变量。 对于设计计算而言，一般给定的是 9mhCh,9meCc,以及进出口 温度中的三个，最终求k,A 对于校核计算而言，给定的一般是A,AmCn,9mCe， 以及2个进 口温度，待求的是

式中， 不是独立变量，因为它取决于 以及换热 器的布置。另外，根据公式(10-15)可是，一旦 和 以及 中的三个已知的话，我们就可以计算出另外一 个温度。因此，上面的三个方程中共有8个未知数，即 需要给定其中的5个变量，才可以计算另外三个变量。 对于设计计算而言，一般给定的是 ，以及进出口 温度中的三个，最终求 对于校核计算而言，给定的一般是 ，以及2个进 口温度，待求的是 m t h h c c t ,t ,t ,t mh h q c mc c q c h h c c t ,t ,t ,t ,k, A,qmhch ,qmccc ,以及t h  ，t h  ，t c  ，t c 中的三个 mh h mc c q c ,q c k, A mh h mc c A,q c ,q c h c t ，t

山西移流字花 SHANXI INSTITUTE OF ENEROY 换热器的热计算有两种方法，一种是平均温差法，另一种是效能- 传热单元数(e-NTU)法 1平均温差法，就是直接应用公式9、10和1011进行热计算， 其具体步骤如下： 对于设计计算(AmhCn,AmeCe,及进出口温度中的三个，求k,A) (1)初步布置换热面，并计算出相应的总传热系数k (2)根据给定条件，由热平衡式9、10求出进、出口温度中的那个 待定的温度 (3)由冷热流体的4个进出口温度确定平均温差△tm (4)由传热方程式(10-10)计算所需的换热面积A,并核算换热面两 侧流体的流动阻力 (⑤)如果流动阻力过大，则需要改变方案重新设计

换热器的热计算有两种方法，一种是平均温差法，另一种是效能- 传热单元数(-NTU)法 1 平均温差法，就是直接应用公式9、10和10-11进行热计算， 其具体步骤如下： 对于设计计算（ ，及进出口温度中的三个，求 ） (1)初步布置换热面，并计算出相应的总传热系数k (2)根据给定条件，由热平衡式9、10求出进、出口温度中的那个 待定的温度 (3)由冷热流体的4个进出口温度确定平均温差 (4)由传热方程式(10-10)计算所需的换热面积A，并核算换热面两 侧流体的流动阻力 (5)如果流动阻力过大，则需要改变方案重新设计。 mh h mc c q c ,q c k, A m t

山多能源宇花 SHANXI INSTITUTE OF ENEROY 对于校核计算 (A,9mhSh,9meC。,及两个进口温度，求tt) ()先假设一个流体的出口温度，按热平衡式计算另一个出口温度 (2)根据4个进出口温度求得平均温差△tm (3)根据换热器的结构，算出相应工作条件下的总传热系数k (4)已知kA和△tm，按传热方程式计算在假设出口温度下的④， (⑤)根据4个进出口温度，用热平衡式计算另一个Φ，，这个值和上面 的①，，都是在假设出口温度下得到的，因此，都不是真实的换热 量 (⑥)比较两个Φ值，满足精度要求，则结束，否则，重新假定出口温度， 重复(1)(6)，直至满足精度要求，一般认为两者误差应小于2%~5%。 从上面的过程可见，平均温差法适用于设计计算，不太适合校 核计算，于是人们找到一种替代方法，即效能-传热单元数法

对于校核计算（ ，及两个进口温度，求 ） (1)先假设一个流体的出口温度，按热平衡式计算另一个出口温度 (2)根据4个进出口温度求得平均温差 (3)根据换热器的结构，算出相应工作条件下的总传热系数k (4)已知kA和 ，按传热方程式计算在假设出口温度下的 (5)根据4个进出口温度，用热平衡式计算另一个 ，这个值和上面 的 ，都是在假设出口温度下得到的，因此，都不是真实的换热 量 (6)比较两个  值，满足精度要求，则结束，否则，重新假定出口温度， 重复(1)~(6)，直至满足精度要求，一般认为两者误差应小于2%~5%。 mh h mc c A,q c ,q c h c t ，t m t m t 1 2 1 从上面的过程可见，平均温差法适用于设计计算，不太适合校 核计算，于是人们找到一种替代方法，即效能-传热单元数法

山西移游李花 SHANXI INSTITUTE OF ENEROY Φ=9mhC,(t%-t%) Φ=qmcc(t&-t&) 2效能-传热单元数法 (1)换热器的效能 和传热单元数NTU 效能C:换热器的实际换热量与最大可能换热量之比 (t-t)mx 反映了换热器里冷热流体进口温度 差的利用率 流体在换热器中可能发生的最大温差 AT Ti (Hot) T Th Te(cold) Te 顺流 逆流

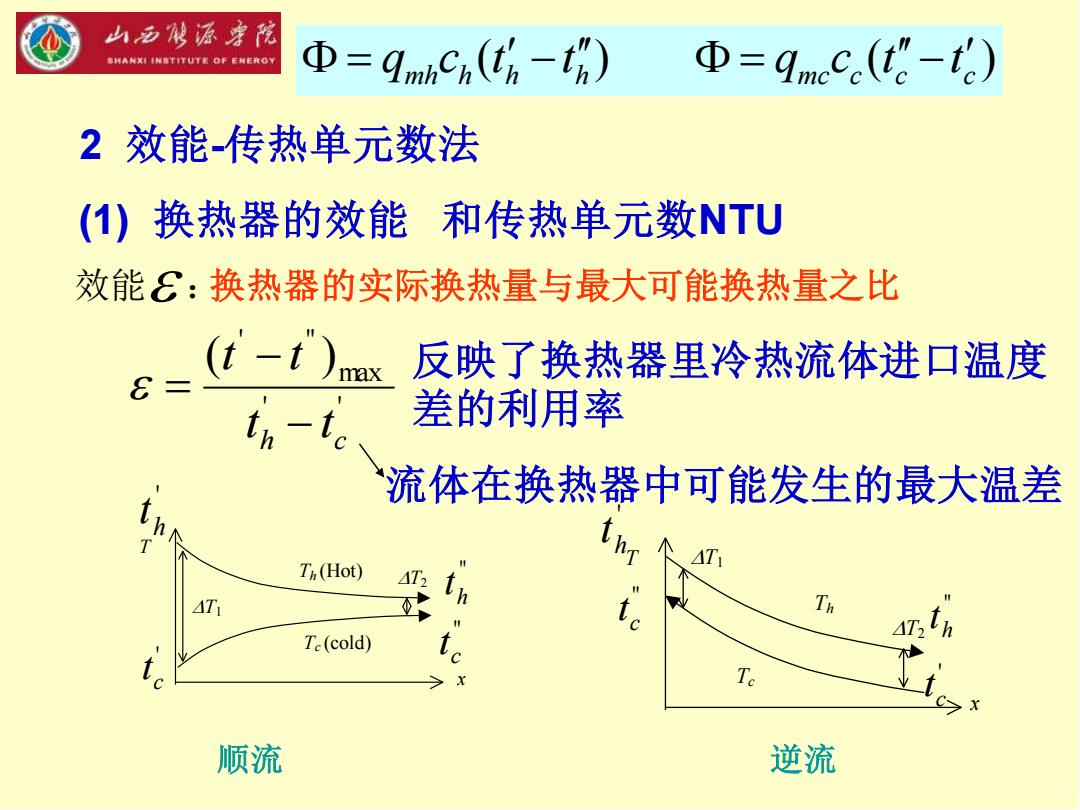
2 效能-传热单元数法 (1) 换热器的效能 和传热单元数NTU ( ) ( ) mh h h h mc c c c  = q c t −t  = q c t−t ' ' max ' " ( ) h c t t t t − −  = x T Th (Hot) Tc (cold) T1 T2 顺流 逆流 x T Th Tc T1 T2 ' 流体在换热器中可能发生的最大温差 h t " c t " h t ' c t ' h t " h t " c t ' c t 效能  ：换热器的实际换热量与最大可能换热量之比 反映了换热器里冷热流体进口温度 差的利用率

山多够源宇花 SHANXI INSTITUT在OF ENERO可 换热器效能的大小与换热器的传热过程有关 那么在未知传热量或出口温度之前，ε又如何计算？和那些因 素有关？ 以顺流换热器为例，并假设9mhCh≤9meCc,则有Cm=Ch C-)_t-t坊 Cmn(%-t&) %-%=(t%-) t6-t 由前面推导的结论，对顺流有： At”_th-t △t' tn-to (-ep62】 根据热平衡关系有：

换热器效能的大小与换热器的传热过程有关 那么在未知传热量或出口温度之前，  又如何计算？和那些因 素有关？ 以顺流换热器为例，并假设 qmhch  qmccc ，则有 ( ) ( )   −   −  =  −   −   = h c h h h c h h h t t t t C t t C t t q q max min  C Ch = min ( ) h h h c t −t =  t −t 由前面推导的结论，对顺流有：       = − = − + − − =     ) 1 1 exp( ) exp ( t ' ' " " h c mh h mc c h c q C q C k A k A t t t t t  根据热平衡关系有： ( ) " ' ' " h h mc c mh h c c t t q C q C t = t + −

山多能源宇院 小 SHANXI INSTITUTE OF ENEROY -。- (mh tn-te in-te 1fg)m(* kA 1-exp 1+ h 1-om-cac) ￡= 1+ h 1+C, C

r r h c h c h h C C C k A C C C C C k A +       − − + = +       − − + = 1 1 exp (1 ) 1 1 exp (1 )  ( )               = − + − − − − h c mh h mc c h h mc c mh h h c q C q C k A t t t t q C q C t t 1 1 exp ' ' " ' ' " ( )               = − + − − + − − − h c mh h mc c h h mc c mh h h h h c q C q C k A t t t t q C q C t t t t 1 1 exp ' ' " ' ' ' ' "               = − +         − + m c c m h h m c c m h h q C q C k A q C q C 1 1 1  1 exp

山西破源宇花 SHANXI INSTITUTE OF ENEROY 上面的推导过程得到如下结果，对于顺流： 当9mhCh≤9meCe 时 1-C) kA C,= min= ￡ C ax C 1+C, 当 9 mhCh≥9 meCe F 时，同样的推导过程可得： C.= C kA Cn 1-exp 1+C,） max 1+C, 上面两个公式合并，可得： kA C 1-exp (1+C,) C, in 8= max 1+C

mh h mc c q c  q c r r c C C C k A +       − − + = 1 1 exp (1 )  当 时，同样的推导过程可得： h c r C C C C C = = max min 上面的推导过程得到如下结果，对于顺流： 当 qmhch  qmccc 时 r r h C C C k A +       − − + = 1 1 exp (1 )  c h r C C C C C = = max min 上面两个公式合并，可得： r r C C C k A +       − − + = 1 1 exp (1 ) min  max min C C Cr =

山多能源宇院 SHANXI INSTITUTE OF ENEROY 1-exp-C 1+C, 换热器效能公式中的飞A依赖于换热器的设计，Cm则依赖于 换热器的运行条件，因此，kA/Cn在一定程度上表征了换热 器综合技术经济性能，习惯上将这个比值（无量纲数）定义为 传热单元数NTU,即 kA NTU= C in 因此， 1-exp[-NTU(1+C)] 1+C, 与顺流类似，逆流时 1-exp|-NTU(1-C)] 1-C,exp-NTU(1-C,)】

r r C C C k A +       − − + = 1 1 exp (1 ) min  换热器效能公式中的 依赖于换热器的设计， 则依赖于 换热器的运行条件，因此， 在一定程度上表征了换热 器综合技术经济性能，习惯上将这个比值（无量纲数）定义为 传热单元数NTU，即 因此， 与顺流类似，逆流时 kA Cmin Cmin kA min NTU C kA =   r r C C + − − + = 1 1 exp NTU(1 )    1 exp NTU(1 ) 1 exp NTU(1 ) r r r C C C − − − − − −  =

山多能源宇院 SHANXI INSTITUTE OF ENEROY 1-exp[-NTU(1+C)] 顺流： 1+C 1-exp-NTU(1-C) 逆流： 1-C.exp-NTU(1-C,) 当冷热流体之一发生相变时，相当于C→0，即 C. m血→0，于是上面效能公式可简化为 max s=1-exp[-NTU] 当两种流体的热熔相等时，即C,=C n=1,8公式可以 简化为 max NTU 顺流： 1-exp-2×NTU 逆流： 2 1+NTU 图10-17~10-21给出了几种流动形式的ε-WTU线算图

  r r C C + − − + = 1 1 exp NTU(1 )    1 exp NTU(1 ) 1 exp NTU(1 ) r r r C C C − − − − − −  = 顺流： 逆流： 当冷热流体之一发生相变时，相当于 ，即 ，于是上面效能公式可简化为 Cmax →  0 max = min → C C Cr  =1−exp− NTU 当两种流体的热熔相等时，即 ， 公式可以 简化为 1 max min = = C C Cr   2 1− exp − 2 NTU  = 1 NTU NTU + 顺流： 逆流：  = 图10-17~10-21给出了几种流动形式的 −NTU 线算图