
第二章导热基本定律及稳态导热 §2-1导热基本定律 一、} 温度场(Temperature field) 某时刻空间所有各点温度分布的总称 温度场是时间和空间的函数,即:t=(x,y,2,T) t一温度; x,乃z一空间坐标;下一时间 稳态温度场 Ot =0 稳态导热 Or Steady-state conduction 非稳态温度场 8t ≠0 → 非稳态导热 Transient conduction 一 维温度场:t=fx,)→一维导热 维温度场:t=f(x,y)→二维导热 二 三维温度场:t=f(x,y,2,)→ 三维导热 特例:一维稳态导热 t=f(x)
§2-1 导热基本定律 第二章 导热基本定律及稳态导热 一、温度场(Temperature field) 某时刻空间所有各点温度分布的总称 温度场是时间和空间的函数,即: t = f (x, y,z, ) t —温度; x, y, z —空间坐标; —时间 稳态温度场 : = 0 稳态导热 t 非稳态温度场 : 0 非稳态导热 t 一维温度场:t = f (x,) 一维导热 二维温度场:t = f (x, y,) 二维导热 三维温度场:t = f (x, y,z,) 三维导热 特例:一维稳态导热 t = f (x) (Steady-state conduction) (Transient conduction)
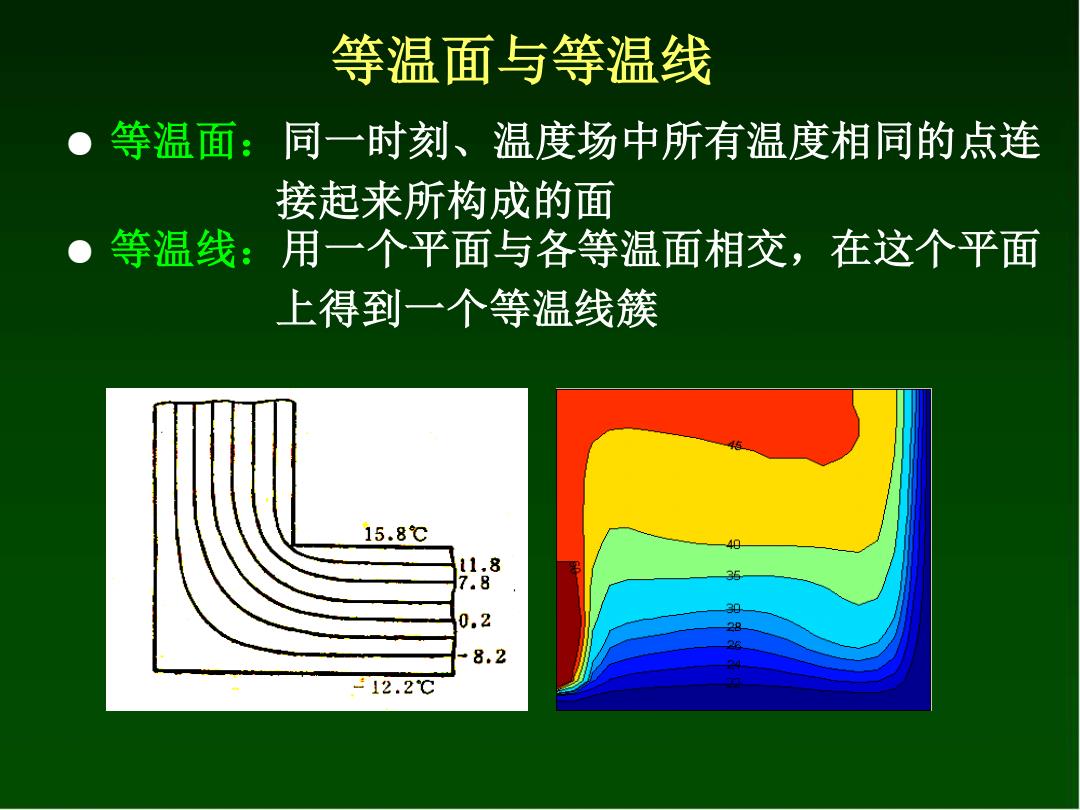
等温面与等温线 等温面:同一时刻、温度场中所有温度相同的点连 接起来所构成的面 等温线:用一个平面与各等温面相交,在这个平面 上得到一个等温线簇 15.8℃ 40 11,8 7.8 30 0.2 28 8.2 212.2℃
等温面与等温线 ● 等温面:同一时刻、温度场中所有温度相同的点连 接起来所构成的面 ● 等温线:用一个平面与各等温面相交,在这个平面 上得到一个等温线簇

等温面与等温线的特点: (1)温度不同的等温面或等温线彼此不能相交 (2)在连续的温度场中,等温面或等温线不会中断, 它们或者是物体中完全封闭的曲面(曲线), 或者就终止与物体的边界上 物体的温度场通常用等温面或等温线表示
(1) 温度不同的等温面或等温线彼此不能相交 等温面与等温线的特点: (2) 在连续的温度场中,等温面或等温线不会中断, 它们或者是物体中完全封闭的曲面(曲线), 或者就终止与物体的边界上 物体的温度场通常用等温面或等温线表示
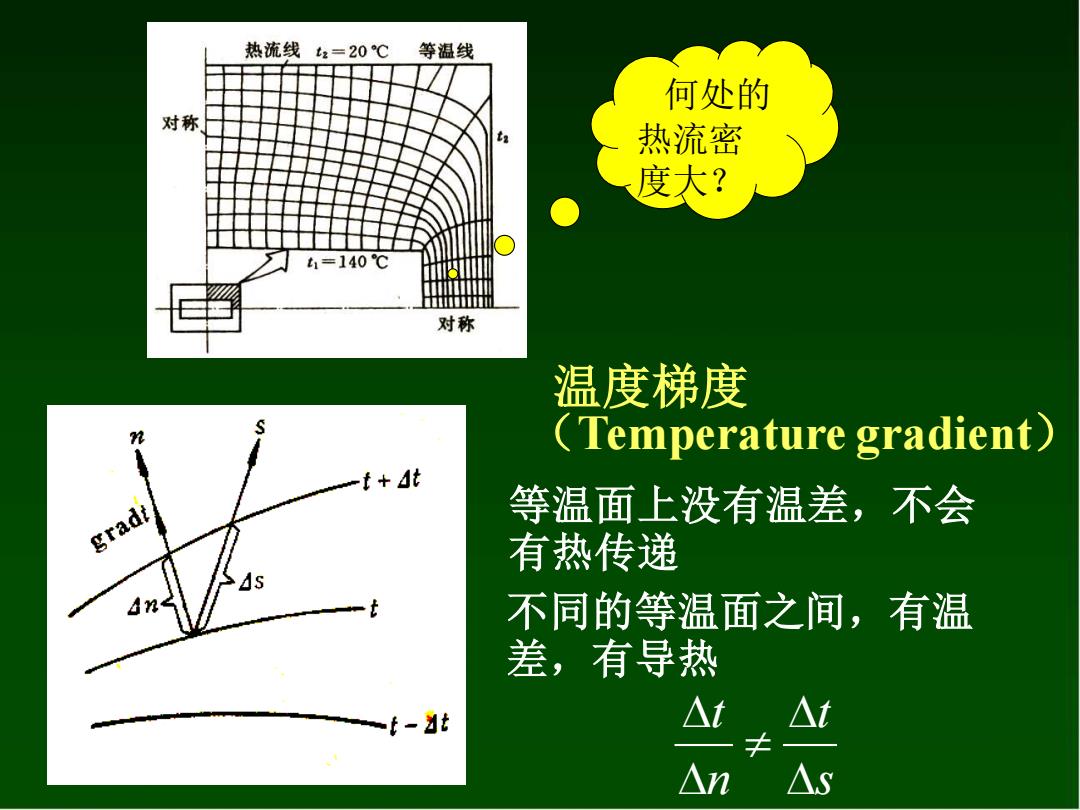
热流线t2=20℃ 等温线 何处的 对称 热流密 度大? t41=140℃ 对称 温度梯度 (Temperature gradient) t+dt gradi 等温面上没有温差,不会 有热传递 不同的等温面之间,有温 差,有导热 - △t △t 卡 △n △s
等温面上没有温差,不会 有热传递 温度梯度 (Temperature gradient) s t n t 不同的等温面之间,有温 差,有导热 何处的 热流密 度大?

温度梯度:沿等温面法线方向上的温度增量 与法向距离比值的极限,gradt △t→ gradt Lim Ot -n=—n n-→0△n On 直角坐标系:(Cartesian coordinates) Ot gradt= Ex y 注:温度梯度是向量;正向朝着温度增加的方向
温度梯度:沿等温面法线方向上的温度增量 与法向距离比值的极限,gradt 直角坐标系:(Cartesian coordinates) n n t n n t t n = = →0 grad Lim k z t j y t i x t t + + grad = 注:温度梯度是向量;正向朝着温度增加的方向

热流密度矢量 Heat flux) 热流密度:单位时间、单位面积上所传递的热量; 不同方向上的热流密度的大小不同 a w/m'] 热流密度矢量:等温面上某点, 以通过该点处最大热 流密度的方向为方向、数值上正好等于沿该方向的热 流密度 直角坐标系中:9=q,i+9,j+9.飞 9,=9c0s日
热流密度矢量 热流密度:单位时间、单位面积上所传递的热量; 直角坐标系中: 热流密度矢量:等温面上某点,以通过该点处最大热 流密度的方向为方向、数值上正好等于沿该方向的热 流密度 不同方向上的热流密度的大小不同 2 q W m q q q i q j q k = x + y + z q q q = q cos (Heat flux) n t dA d q

二、导热基本定律Fourier'slaw) 1822年,法国数学家傅里叶(Fourier)在实验研究 基础上,发现导热基本规律一 傅里叶定律 导热基本定律:垂直导过等温面上 某点的热流密度,正比于该处的温 度梯度,方向与温度梯度相反 g=-Agrad t [W/m2] 2:热导率(导热系数)[w/mC】 ●负号的含义:热量传递方向指向温度降低的方向,与温度梯度方向相反 ●热流方向与等温线(面)垂直,热流密度适量的走向可用热流线来表示, 热流线是一组与等温线处处垂直的曲线,通过平面上任一点的热流线与该点 的热流密度矢量相切
二、导热基本定律(Fourier’s law) 1822年,法国数学家傅里叶(Fourier)在实验研究 基础上,发现导热基本规律 —— 傅里叶定律 导热基本定律:垂直导过等温面上 某点的热流密度,正比于该处的温 度梯度,方向与温度梯度相反 - grad [W m ] 2 q = t : 热导率(导热系数) W (m C) (Thermal conductivity) ⚫负号的含义:热量传递方向指向温度降低的方向,与温度梯度方向相反 ⚫热流方向与等温线(面)垂直,热流密度适量的走向可用热流线来表示, 热流线是一组与等温线处处垂直的曲线,通过平面上任一点的热流线与该点 的热流密度矢量相切

直角坐标系中: g-q.ita.Jtq.K--AQj-AOJ-AOR &x Oz 注:傅里叶定律只适用于各向同性材料 各向同性材料:热导率在各个方向是相同的
直角坐标系中: k z t j y t i x t q q i q j q k x y z − − = + + = − z t q y t q x t qx y z = − = − = − ; ; 注:傅里叶定律只适用于各向同性材料 各向同性材料:热导率在各个方向是相同的

有些天然和人造材料,如:石英、木材、叠层塑料板、叠层 金属板,其导热系数随方向而变化 各向异性材料 各向异性材料中,热流密度方向不仅与温度梯度方向有关,还 与热导率的方向性有关,因此热流密度矢量与温度梯度不一定 在同一条直线上: -9.=a 大入y Ox -9,=入 +7y + -q.=元 8t Ox
有些天然和人造材料,如:石英、木材、叠层塑料板、叠层 金属板,其导热系数随方向而变化 —— 各向异性材料 各向异性材料中,热流密度方向不仅与温度梯度方向有关,还 与热导率的方向性有关, 因此热流密度矢量与温度梯度不一定 在同一条直线上: z t y t x t q z t y t x t q z t y t x t q z zx zy zz y y x y y y z x x x x y x z + + − = + + − = + + − = x y qx qy q n x y

问题: 已知下图平板中的温度分布可以表示成如下形式: t=Cx2+C2 其中C1、C,和平板的导热系数为常数,计算通过X=0 截面处的热流密度为多少? Ot 8x x=0=2C4x-0=0
问题: 已知下图平板中的温度分布可以表示成如下形式: 2 2 1 t = c x + c 其中C1、C2和平板的导热系数为常数,计算通过X=0 截面处的热流密度为多少? 2 0 0 = 1 0 = x= x= c x x t